Пример 1.25

1. Пусть (p,п) и (f,п) – множества упорядоченные по отношению п из примера 1.21. Диаграммы Хассе этих множеств представлены на рис. 1.6 и 1.7.

2. Пусть   {1, 2, 3}. На множестве  2^   {, {1}, 2, 3, 1, 2, 1, 3, 2,3, 1, 2, 3 зададим отношение частичного порядка "быть подмножеством", то есть x   y  тогда и только тогда, когда  x    y. Диаграмма Хассе для этого множества представлена на рис. 1.8, а.  

3. Пусть   1, 2, 3, 5, 6, 10, 15, 30. На этом множестве (делителей числа 30) зададим отношение частичного порядка:  x | y тогда и только тогда, когда x делит  y. Диаграмма Хассе для этого множества представлена на рис. 1.8, б.

4. На числовом множестве   1, 2, 3, 4, 5, 6, 7, 8 рассмотрим отношение   (меньше или равно). Диаграмма Хассе для этого множества представлена на рис. 1.8, в.

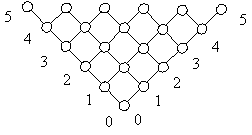Рис. 1.6. Диаграмма Хассе множества P

 

 

Рис. 1.7. Диаграмма Хассе множества F

 

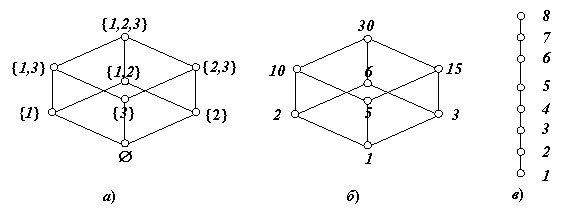
Рис. 1.8. Диаграммы Хассе упорядоченных множеств 2^, X, Y.

Два частично упорядоченных множества  и  называются изоморфными, если существует биекция  :   , сохраняющая отношение частичного порядка. Иначе: x₁   _X   x₂ тогда и только тогда, когда  x₁   _Y  x₂,  где  _X – отношение частичного порядка на множестве , а  _Y – отношение частичного порядка на множестве .

Такая биекция для множеств  и 2^  из примера 1.22 (2, 3)  существует. Например:

          , <6, {1, 2}>, <10, {1, 3}>, <15, {2, 3}>, <30, {1, 2, 3}>}.

Диаграммы Хассе для этих множеств одинаковы, вернее имеют одинаковую структуру.

Утверждение 1.10. Всякое частично упорядоченное множество  изоморфно некоторой системе подмножеств множества , частично упорядоченной отношением включения.

Построим такую систему S.

Для каждого элемента a   рассмотрим множество S_a  {x  x   и x  a}. Тогда S_a   , а S = {S_a  a  } – совокупность всех таких подмножеств.

Докажем, что система S, частично упорядоченная отношением включения, изоморфна .

Рассмотрим отображение  :   S, такое, что a = S_a, то есть <a, S_a>  .

Покажем, что  – биекция. Пусть a, b  . Рассмотрим пары <a, S_a>    и <b, S_b>  . Предположим, что S_a = S_b. Тогда, так как   рефлексивно, то есть a    a, то a  S_a, а значит, что a  S_b, следовательно, a   b (<a, b>   ). Повторив эти рассуждения для b, получим b   a (<b, a>  ). Так как отношение частичного порядка    антисимметрично, то из <a, b>     и <b, a>     следует, что a = b. То есть  – инъективно.

По построению для любого S_a  S  <a, S_a>  , то есть  – сюръективно. Таким образом,  – биекция.

Покажем теперь, что  сохраняет отношение частичного порядка. Пусть <a, b>  , иначе: a   b. Возьмем x   a. Так как   транзитивно, то из x   a и a   b следует, что x   b, отсюда x  S_a и x  S_b, то есть S_a  S_b. С другой стороны, если S_a   S_b и так как a  S_a, то a  S_b, то есть a   b.

Таким образом,  изоморфно S.

Пример 1.26

Для множества   1, 2, 3, 5, 6, 10, 15, 30} , на котором задано отношение частичного порядка x    y  тогда и только тогда, когда  x делит  y, изоморфным будет частично упорядоченное отношением включения множество:

S = {{1}, {1, 2}, {1, 3}, {1, 5}, {1, 2, 3, 6}, {1, 2, 5, 10}, {1, 3, 5, 15}, 1, 2, 3, 5, 6, 10, 15, 30}}.

Следуя доказательству утверждения 1.8 нетрудно построить биекцию , сохраняющую изоморфизм, а также явно задать множество   :

<1,1>, <1,2>, <1,3>, ...,<1,30>, <2,2>, <2,6>, <2,10>, <2,30>, <3,6>, <3,15>, <3,30>, <5,10>, <5,15>, <5,30>, <6,30>, <10,30>, <15,30>, <30,30>}.

Классы бинарных отношений, не являющиеся эквивалентностью или частичным порядком

В качестве примеров приведем определения некоторых других,  бинарных отношений, важных в математике:

1) бинарное отношение называется толерантностью, если оно рефлексивно и симметрично (транзитивность не выполняется);

2) бинарное отношение называется квазипорядком (предпорядком), если оно рефлексивно и транзитивно (не выполняются ни симметричность, ни антисимметричность);

3) бинарное отношение называется строгим порядком  (предпорядком) , если оно иррефлексивно, антисимметрично и транзитивно;

4) бинарное отношение называется строгим квазипорядком , если оно иррефлексивно  и транзитивно (не выполняются ни симметричность, ни антисимметричность).

1.6. Алгебраические операции

           n-арная алгебраическая операция

           Задание операции таблицей Кэлли

           Свойства, терминология

           Порядок выполнения алгебраических операций

          Степени

n-арная алгебраическая операция

В курсах математики встречаются различные алгебраические операции. В общем случае алгебраическую операцию можно задать следующим образом.

Пусть дано множество M. n-арной алгебраической операцией на множестве M называется функция типа  : Mⁿ  M.

Если n = 1, то операция называется унарной, при n = 2 – бинарной.

На множестве M может быть задано конечное число операций различной арности, которые образуют множество  = {₁, ₂,…,_n}.