К теме комбинаторика
4. Бином Ньютона
Из школьного курса алгебры хорошо известны формулы:
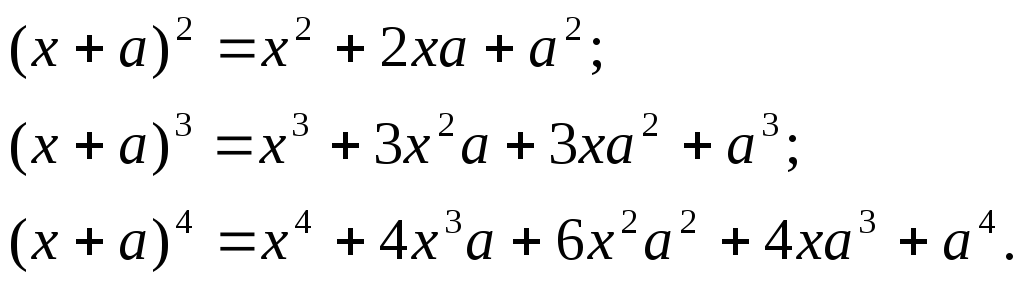
Последнюю формулу можно получить,
умножив
на
.
Обобщим эти формулы для любого целого
неотрицательного показателя n,
т.е. в правой части равенства
(11)
выполним умножение и приведем подобные члены.
Теорема 7. Для любого целого неотрицательного п справедлива формула
(12)
Равенство
(12) принято называть биномом Ньютона,
его правую часть – биномиальным
разложением или разложением бинома, а
комбинаторные числа
,
,…,
т.е. коэффициенты разложения, –
биномиальными коэффициентами
При
из формулы (12) следует
Общий член разложения бинома имеет вид
,
Приведем основные свойства биномиальных коэффициентов
1º.
2º.
3º
4º.
5º.
6º.
7º.
Задача
9.
Доказать тождество
.
5. Полиномиальная формула. Формула включений и исключений.
При преобразовании выражений часто возникает необходимость возвести в степень сумму нескольких слагаемых. Для небольшого числа слагаемых это сделать легко, достаточно несколько раз применить формулу бинома Ньютона. Так, степень трех слагаемых можно представить в виде:
Затем по формуле бинома
Ньютона раскрыть скобки в каждом
выражении
и привести подобные
члены.
Для большого числа слагаемых и при больших значениях n такой способ вычисления слишком громоздок. Кроме того, он не позволяет непосредственно узнать, с каким коэффициентом входит в разложение тот или иной конкретный член. Поэтому для возведения в степень суммы нескольких слагаемых найдем общую формулу, аналогичную формуле бинома Ньютона.
Теорема 7.
Формула бинома Ньютона является частным
случаем полиномиальной формулы. По этой
причине для удобства запоминания
полиномиальной формулы ее коэффициенты
часто обозначают
,
полагая
.
В результате формула выглядит так:
.
Свойства полиномиальных коэффициентов.
1º
2º.
3º.
4º..
Пусть даны два конечных множества
и
.
В том случае, когда
,
число элементов
,
принадлежащих объединению
,
равно сумме числа элементов этих
множеств:
.
Число элементов в объединении n
множеств, которые попарно не пересекаются,
находится аналогично:
,
где
,
,
.
В том случае, когда
,
как видно из рисунка 1, каждый элемент
пересечения
входит в сумму
дважды. Поэтому
(23)
Заметим, что формула (23) включает и
случай, когда
.
Обобщим формулу (23).
Теорема 8.
Следствие. Пусть
– конечное множество и
– его подмножества. Тогда
Доказанная формула (24) называется формулой включений и исключений.
Широкое применение в комбинаторике
получил частный случай формулы включений
и исключений, в которой число
элементов, обладающих свойствами
,
зависит не от самих этих свойств, а от
их числа.
Задача 10 В олимпиаде по математике принимало участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну – по геометрии и одну по тригонометрии. В результате проверки оказалось, что задачу по алгебре решили 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек, по алгебре и геометрии – 7, по алгебре и тригонометрии – 8, по геометрии и тригонометрии – 9 человек. Известно, что ни одной задачи не решили трое. Сколько учащихся решили все три задачи? Сколько учащихся решили ровно две задачи?
6. Разупорядочения. Пусть дано упорядоченное n-множество X. Разупорядочением множества X называется такая перестановка его элементов,
Теорема 9.. (27)
Примечание.
Впервые комбинаторное число
нашел французский математик П.Монмор
при решении так называемой «задачи о
встречах». Найденное число называют
также числом
беспорядков.
Это название объясняет такая задача.
Задача 11 (задача о беспорядках).
Имеется
различных предметов
и
различных ячеек
.
Требуется разместить предметы по ячейкам
так, чтобы никакой предмет
не попал в ячейку
.
Сколько существует таких способов
размещения?
Решение.
Теорема 10. Пусть
– число перестановок
элементов, при которых ровно
элементов остаются на своих местах,
тогда имеет место равенство
.
(28)
Доказательство.
Задача 12. Рассеянный почтальон должен разнести 12 писем по 12 адресам. Сколькими способами он может разложить письма по почтовым ящикам так, чтобы
а) ни один адресат не получил адресованное ему письмо;
б) ровно 5 человек получили адресованные им письма;
в) хоть один адресат получил адресованное ему письмо;
г) ровно один адресат получил адресованное ему письмо?
.