Производная функции на интервале

Вернемся к нашей функции . Рассмотрим ее табличное представление на интервале [-0.2, 1.4] .

xi	-0.2	0	0.2	0.4	0.6	0.8	1	1.2	1.4
f(xi)	0.04	0	0.04	0.16	0.36	0.64	1	1.44	1.96

Пусть необходимо построить график производной этой функции.

Для этого необходимо найти значения производных в каждой точке функции. Левые это будут производные или правые, принципиально не важно. Важно то, что для точки не существует левой производной, а для точки — правой. Это связано с тем, что в общем случае мы не знаем, как ведет себя функция за пределами заданного интервала. Хотя мы легко можем продолжить зависимость влево и вправо, на практике эта зависимость, как правило, неизвестна.

Итак, расчет левых производных дает зависимость:

	-0.2	0	0.2	0.4	0.6	0.8	1	1.2	1.4
	0.04	0	0.04	0.16	0.36	0.64	1	1.44	1.96
	---	-0.2	0.2	0.6	1	1.4	1.8	2.2	2.6

Для правых производных:

	-0.2	0	0.2	0.4	0.6	0.8	1	1.2	1.4
	0.04	0	0.04	0.16	0.36	0.64	1	1.44	1.96
	-0.2	0.2	0.6	1	1.4	1.8	2.2	2.6	---

Обратите внимание, что в обоих случаях зависимость является линейной, что соответствует теории.

Из школьного курса математики известно, что особые точки функций и их экстремумы определяются характером первой и второй производной. В нашем случае анализ производной показывает, что в окрестности точки находится экстремум функции, а именно минимум. Это также соответствует действительности.

Решение типовых задач

Задача 1. Дана табличная функция на интервале [a,b]. Найти производные функции слева и справа от любой точки на интервале.

Решение.

Используем данные, полученные в лабораторной работе №5 при табулировании функции Пример чтения данных из файла был описан в листинге 26 и здесь не приводится. Будем считать производные для точки при .

Листинг 27

/*Производная функции в точке*/

#include <fstream.h>

#include <math.h>

void main( void )

{

// Массив для хранения значений аргумента и функции

double nArray[11][2];

// Прочитать данные табличной функции из файла,

// занести их в массив nArray и вывести на экран (Листинг 26)

double dResultLeft, dResultRight;

// Расчет производной слева

dResultLeft = ( nArray[5][1] - nArray[4][1] ) / ( nArray[5][0] - nArray[4][0] );

// Расчет производной справа

dResultRight = ( nArray[6][1] - nArray[5][1] ) / ( nArray[6][0] - nArray[5][0] );

// Вывод результата

cout << "\n\nfor x = " << nArray[5][0] << "\n";

cout << "y`(x)Left = " << dResultLeft << "\ny`(x)Right = ";

cout << dResultRight << "\n";

}

Задача 2. Дана табличная функция [a,b]. Найти значения производной функции в каждой точке интервала. Занести полученные данные в файл. Построить график производной.

Решение.

Как и в предыдущей задаче воспользуемся данными, полученными в лабораторной работе №5 при табулировании функции . Программный код, осуществляющий чтение приводить не будем. Считаем, что данные прочитаны и занесены в массив nArray.

Листинг 28

/*Производная функции на интервале*/

#include <fstream.h>

#include <math.h>

void main( void )

{

// Массив для хранения значений аргумента и функции

double nArray[11][2];

// Прочитать данные табличной функции из файла,

// занести их в массив nArray и вывести на экран (Листинг 26)

// Вывод заголовка

cout << "\nDerivative\nx\ty`\n";

// Массив для хранения результата

double dResult[10];

ofstream File("derivative.txt");

for ( i = 0; i < 10; i++ )

{

// Расчет производной справа

dResult[i]= (nArray[i+1][1] - nArray[i][1])/(nArray[i+1][0] - nArray[i][0]);

// Вывод результата на экран

cout << nArray[i][0] << "\t" << dResult[i] << "\n";

// Вывод результата в файл

File << nArray[i][0] << "\t" << dResult[i] << "\n";

}

File.close();

}

Содержимое файла derivative.txt:

0 0.2

0.2 0.6

0.4 1

0.6 1.4

0.8 1.8

1 2.2

1.2 2.6

1.4 3

1.6 3.4

1.8 3.8

График производной представлен на рис. 19

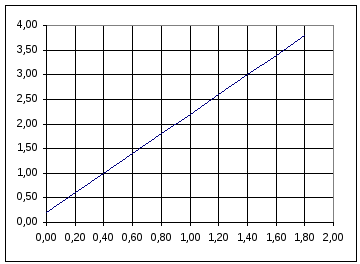
Рис. 19