5. Системи координат в просторі геометричних векторів.

Повернемось у тривимірний простір геометричних векторів. Очевидно, базис в ньому утворюють довільні три не компланарні вектори (нагадаємо, що компланарними називаються три вектори, які паралельні одній площині). Отже, виберемо три не компланарних вектори та зведемо їх до спільного початку – деякої точки О. Одержимо загальну афінну систему координат. Якщо три базисних вектори взаємно перпендикулярні, система координат називається прямокутною. І нарешті, якщо у прямокутній системі координат базисні вектори мають одиничну довжину, маємо знайому із школи ПДСК – прямокутну декартову систему координат. Базисні вектори в ній позначаються, як вже згадувалось вище, , а координати вектора називаються відповідно абсциса, ордината та апліката. Будемо позначати їх наступним чином: . Це означає, що .

6. Добутки векторів.

В даному розділі розглядаються вектори із простору геометричних векторів.

6.1. Скалярний добуток векторів.

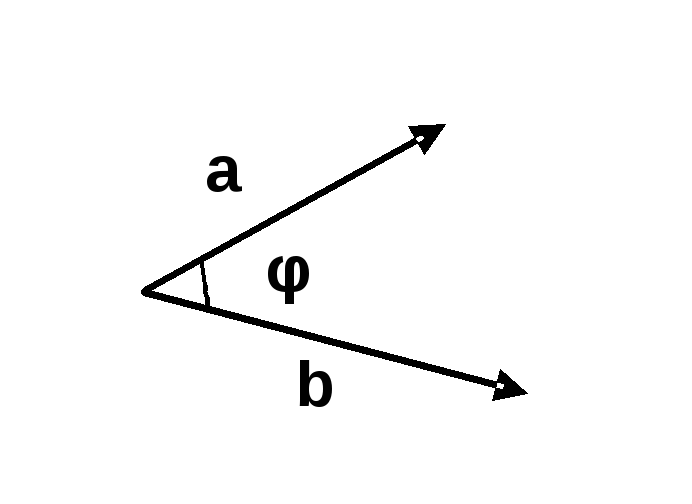
Означення 14. Скалярним добутком двох векторів називається число , рівне: , де – кут утворений векторами та , а через позначено довжину вектора .

Н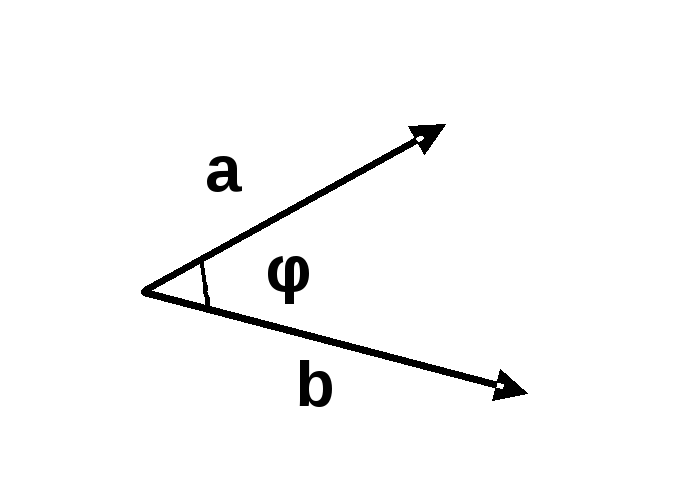еважко зрозуміти, що скалярний добуток двох ненульових векторів рівний 0 тоді і тільки тоді, коли вектори ортогональні:

Означення 2. Ортом вектора називається вектор одиничної довжини співнапрямлений з вектором . Тобто .

Означення 3. Проекцією вектора на напрямок вектора називається число . Звідси легко одержати, що

Зауваження. З означення випливає, що проекція додатна, якщо кут між векторами та гострий, та від’ємна, у разі, коли кут тупий.

Властивості скалярного добутку векторів.

1. – комутативність скалярного добутку очевидно випливає з його означення;

2. – скалярний множник можна виносити за знак скалярного добутку (доведіть це самостійно);

3. – дистрибутивність скалярного добутку випливає із властивостей проекцій, які вивчались у курсі шкільної програми.

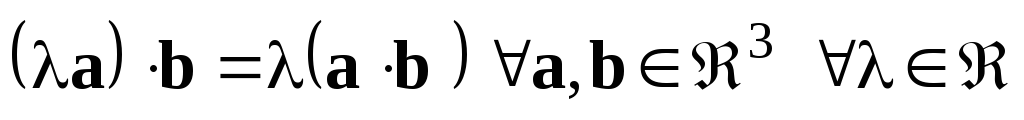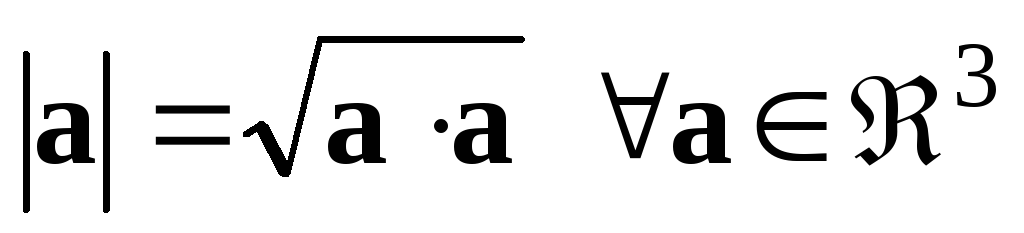4. – скалярний добуток визначає квадрат довжини вектора.

Нехай у просторі геометричних векторів вибрана деяка ПДСК. Як визначити скалярний добуток векторів та , якщо відомі їх координати? Отже, нехай маємо вектори та . Визначимо скалярний добуток цих векторів, скориставшись властивостями скалярного добутку:

Зауваження. Зверніть увагу, що одержана формула має місце лише для ПДСК. У загальній афінній системі координат ми мали б враховувати кути між базисними векторами.

Таким, чином у прямокутній декартовій системі координат справедлива наступна формула скалярного добутку двох векторів:

(1)

Формула (1) дає важливі наслідки, зокрема, довжина вектора визначається через його координати наступним чином: (2)

Для кута між двома векторами маємо формулу:

(3)

Означення 15. Напрямними косинусами вектора називаються косинуси кутів, утворених вектором з ортами ПДСК. Ці кути позначаються відповідно , та , отже, з формули (3) випливає: , аналогічно , . Звідси маємо основну властивість напрямних косинусів:

(4)

Таким чином, якщо , то – тобто, напрямними косинусами орта є його координати.

Приклади.

1. Знайдемо орт вектора . Маємо , тому .

2. Кут між ортами і рівний . Знайти скалярний добуток цих векторів. Знаходимо за означенням .

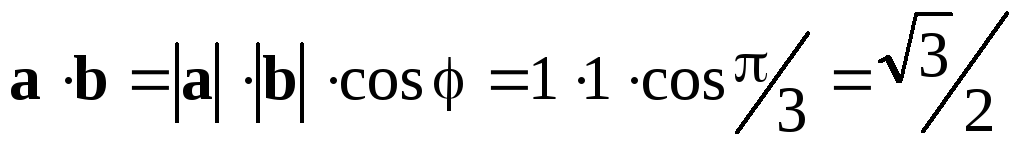3. Нехай , 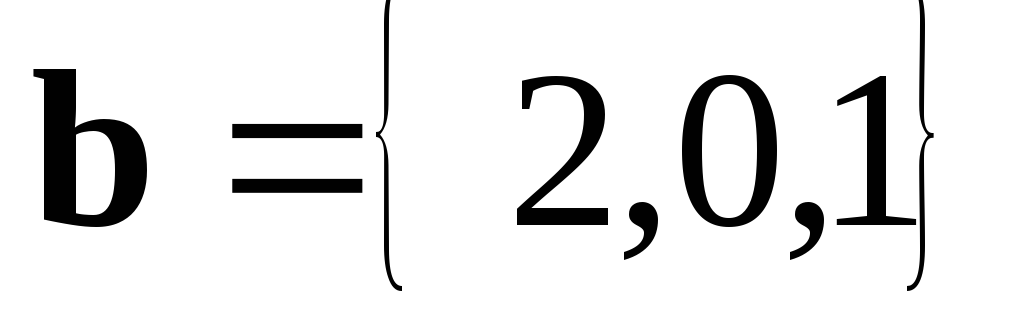. Знайдемо кут між цими векторами. З формули (3) одержимо , отже, .

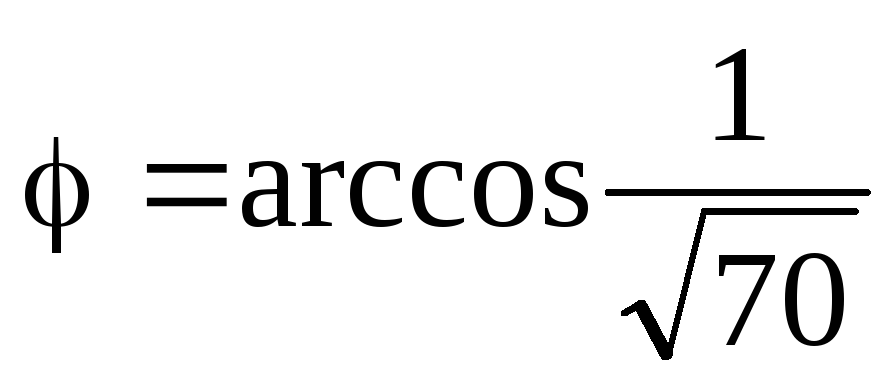4. Знайдемо скалярний добуток 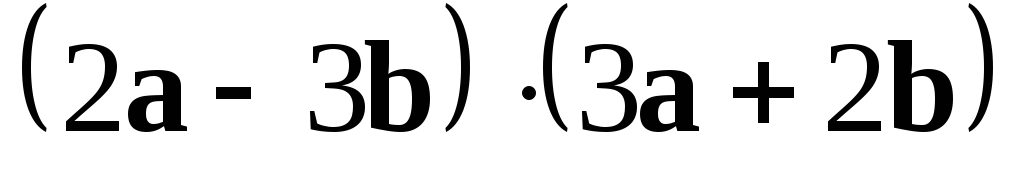для векторів з прикладу 3.

В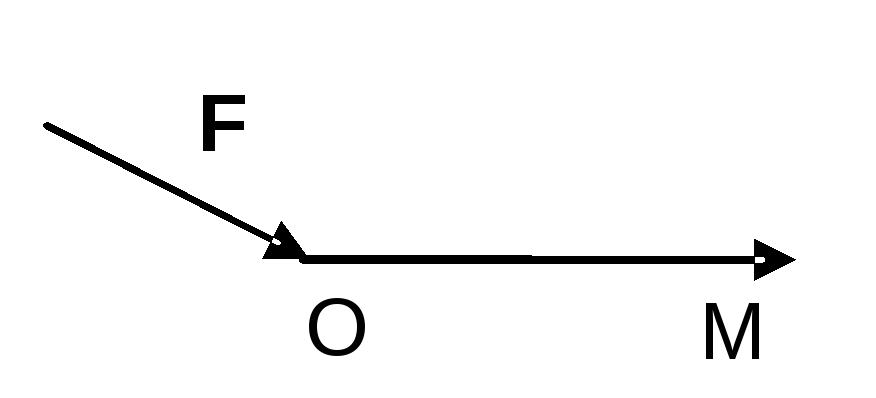иконаємо спочатку дії над векторами: .

Фізичний зміст скалярного добутку.

Якщо під впливом сили деяка матеріальна точка переміщається з положення у положення , то робота цієї сили по переміщенню даної точки рівна скалярному добутку сили та вектора переміщення точки: .

(див мал.)