Лекція 2. Простір геометричних векторів. Добутки векторів.

1. Вектори. Операції з векторами.

Означення 1. Геометричним вектором називатимемо напрямлений відрізок у тривимірному просторі.

Отже, вектор характеризується напрямком та довжиною і цілком визначається двома точками: одна задає початок вектора, друга – його кінець. Як відомо, аналітично вектори позначаються цими двома точками, наприклад, вектор .

Означення 2. Два геометричних вектори називаються рівними, якщо вони мають однакову довжину та напрямок – тобто лежать на паралельних прямих. (Це так звані вільні вектори з довільною точкою прикладення. У фізиці, крім них розглядаються ще ковзні вектори, тобто напрямлені вздовж однієї прямої).

Отже рівні вектори можуть бути суміщені паралельним перенесенням, тобто точка-початок вектора не є визначальною, тому інколи вектор позначають однією літерою, наприклад, вектор або .

Означення 3. Нуль-вектором називають вектор , який має нульову довжину та невизначений напрямок.

Означення 4. Протилежним вектором до вектора називають вектор , такий що .

Означення 5. Вектори та називаються колінеарними (позначається цей факт так: ), якщо вони лежать на паралельних прямих.

У множині геометричних векторів визначені лінійні операції над ними – додавання векторів та множення вектора на скаляр (дійсне число). Правила визначення результуючого вектора при цих операціях добре відомі зі шкільної програми, тому не будемо тут їх повторювати.

Виявляється, що множина геометричних векторів є лише однією з реалізацій, моделлю більш загального математичного поняття – лінійного або векторного (на цей час для нас ці слова будуть синонімами!) простору.

Всі елементи векторного простору називають векторами (інколи незважаючи на природу цих елементів).

2. Лінійно залежні та лінійно незалежні системи векторів.

Розглянемо довільний векторний простір . Зафіксуємо в ньому деяку підмножину (систему) векторів

. З означення операцій над векторами цього простору випливає можливість утворювати лінійні комбінації векторів, тобто – лінійна комбінація векторів простору . Числа називають коефіцієнтами лінійної комбінації.

Означення 7. Лінійна комбінація називається тривіальною, якщо всі її коефіцієнти рівні нулю.

Зауваження. Очевидно, що тривіальна лінійна комбінація – це нульовий вектор.

Означення 8. Система векторів називається лінійно незалежною, якщо лише тривіальна лінійна комбінація векторів цієї системи рівна нуль-вектору.

Зауваження. Іншими словами, система векторів лінійно незалежна, якщо з того, що випливає: .

Означення 9. Система векторів називається лінійно залежною, якщо існує нетривіальна лінійна комбінація векторів цієї системи, рівна нуль-вектору.

Приклади.

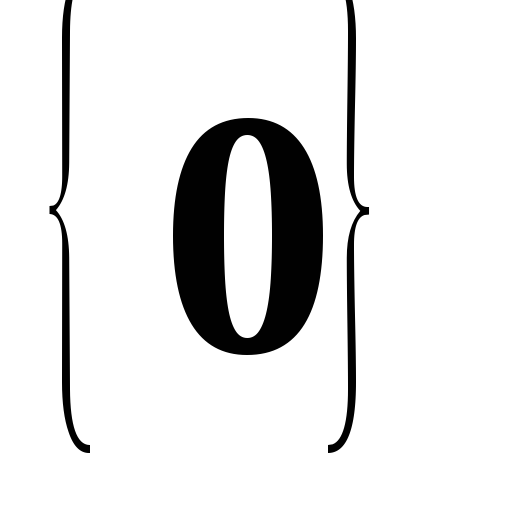1. – лінійно залежна система, оскільки існує нетривіальна лінійна комбінація .

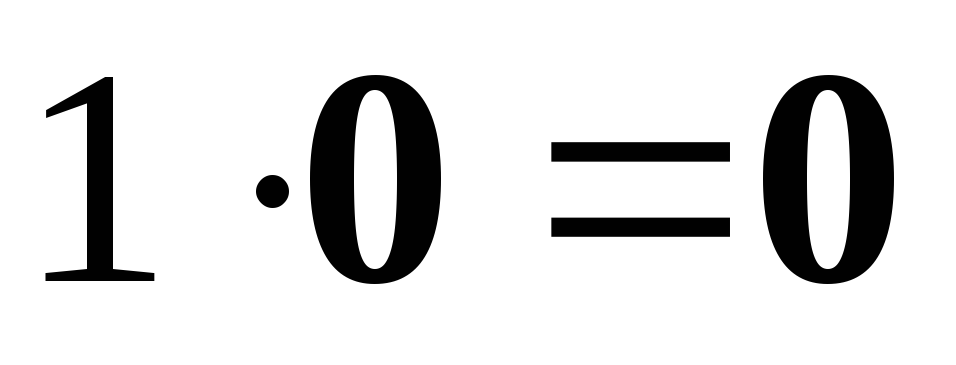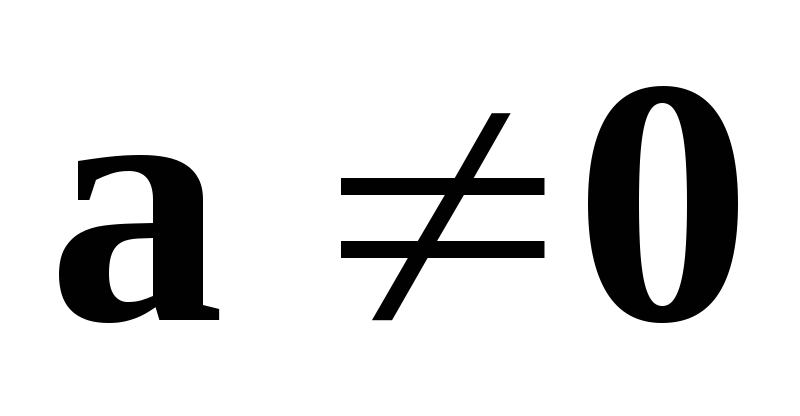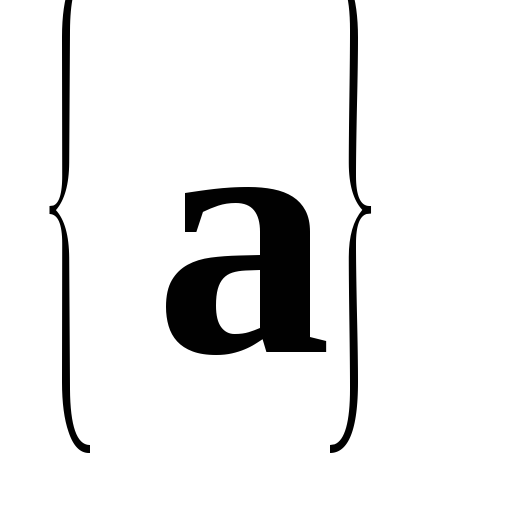2. Нехай . Тоді – лінійно незалежна система, оскільки з рівності 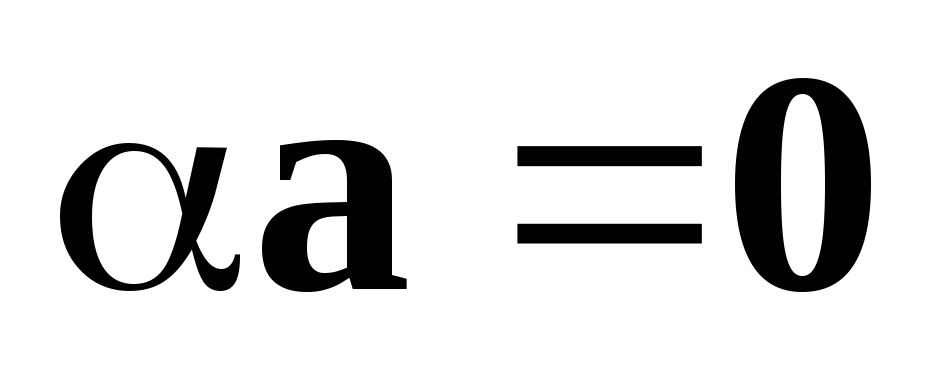обов’язково випливає, що .

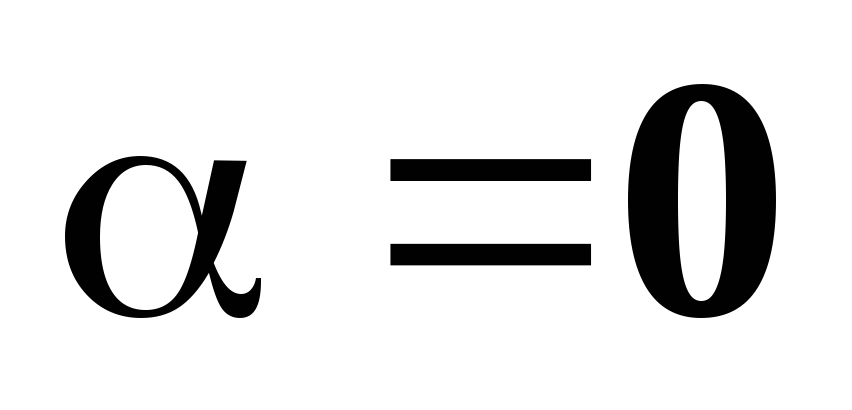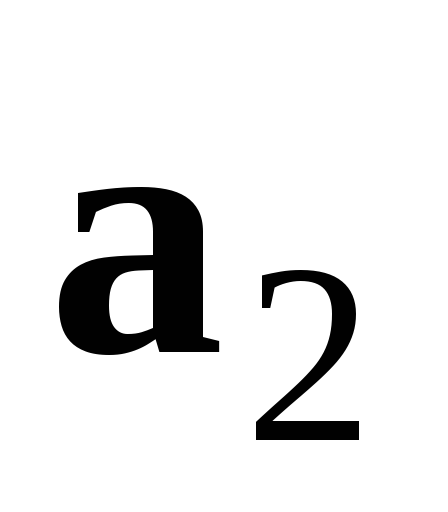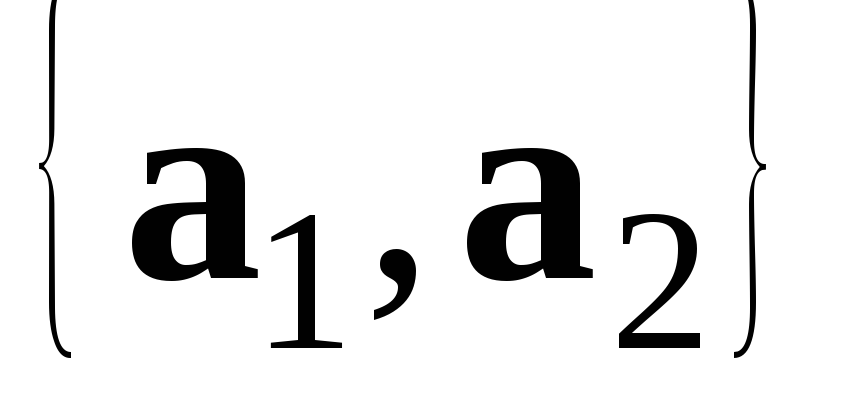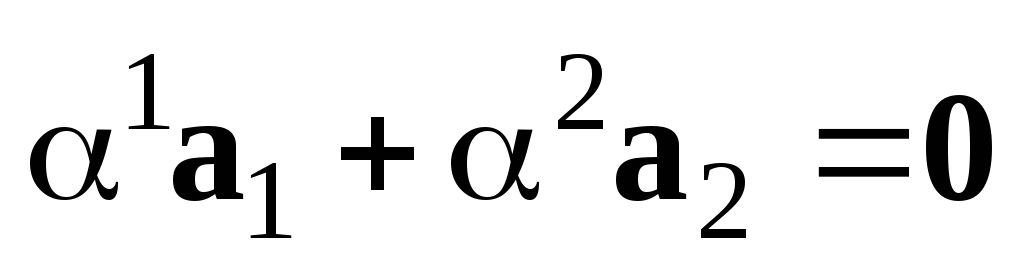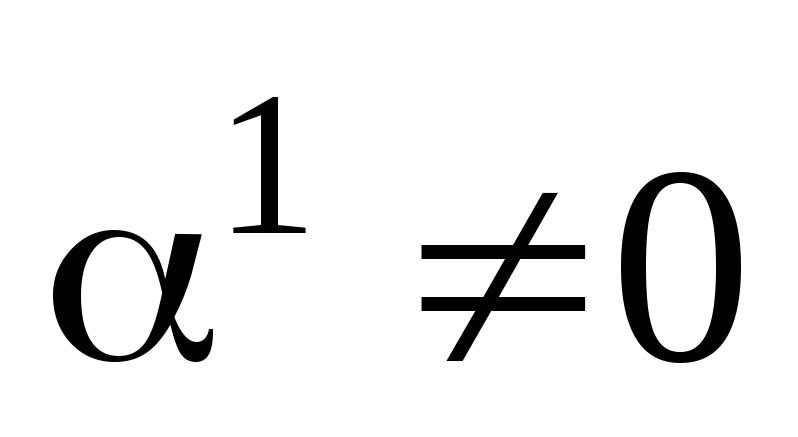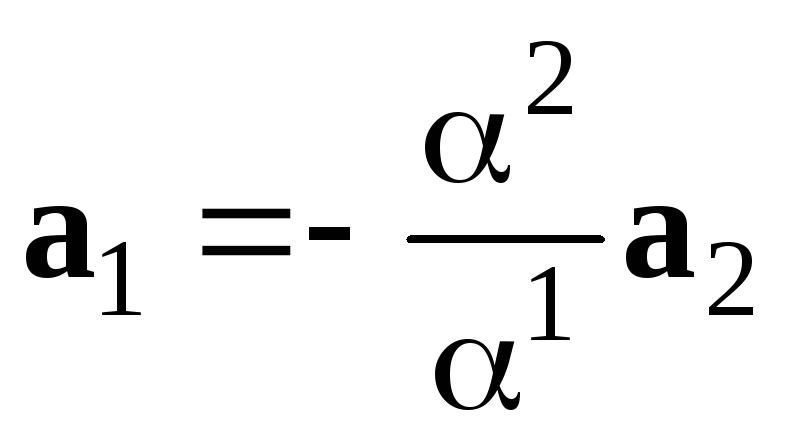3. Нехай та два не колінеарних геометричних вектора. Тоді – лінійно незалежна система векторів. Доведемо це від супротивного, тобто припустимо існування деякої нетривіальної лінійної комбінації цих векторів, яка рівна нулю: . Нехай тут . Тоді , що означає колінеарність векторів. Одержана суперечність свідчить про лінійну незалежність системи векторів .
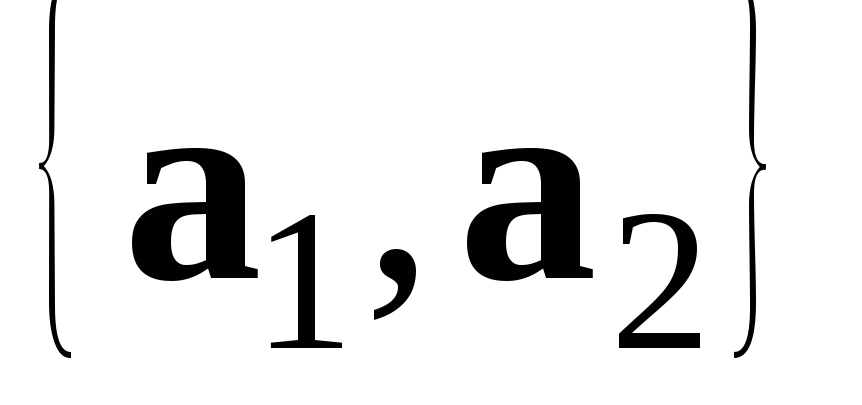