12

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО КУРСУ

«НАДЁЖНОСТЬ И ДИАГНОСТИКА

ТЕХНОЛОГИЧЕСКИХ СИСТЕМ»

ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО КУРСУ

«НАДЁЖНОСТЬ И ДИАГНОСТИКА

ТЕХНОЛОГИЧЕСКИХ СИСТЕМ»

1. НадёжностЬ станков

1.1. Основные показатели надёжности станков и их нормирование.

1.2. Причины потери станком работоспособности.

1.3. Расчёты на износ сопряжений станков.

1.4. Основные методы повышения надёжности станков.

2. АНАЛИЗ НадёжностИ РЕЖУЩЕГО инструментА

2.1. Виды и причины отказов режущего инструмента.

2.2. Надёжность режущего инструмента.

2.3. Надёжность работы фрез.

3. ОБЕСПЕЧЕНИЕ надёжностИ технологическОГО процессА

3.1. Надёжность технологического процесса.

3.2. Остаточные и побочные явления технологических процессов.

Алгоритм расчёта параметров процесса зенкерования с целью обеспечения надёжности технологического процесса

РАСЧЁТНЫЕ ЗАВИСИМОСТИ ДЛЯ ЗЕНКЕРОВАНИЯ

Расчёт параметров сечения среза и угла схода стружки

1. Расчёт главного угла в плане φ зуба зенкера

, (1)

где φ₀ – главный угол зуба зенкера в плане без учета угла наклона режущей кромки λ, рад.

2. Расчёт ширины среза b₁

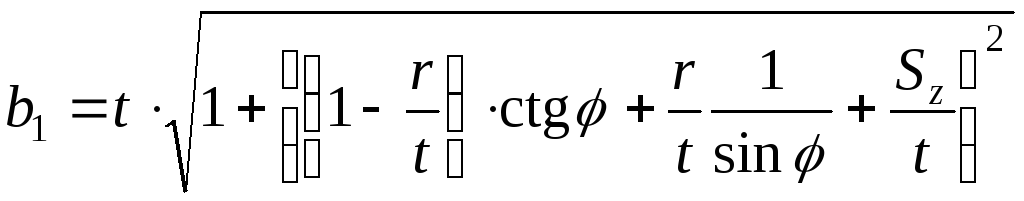, (2)

где t – глубина резания, м; r – радиус при вершине зуба, м; s_z – подача на зуб инструмента, м;

s_z =, (3)

здесь s₀ – подача на оборот, м; z – число зубьев зенкера.

3. Расчет толщины среза a₁

, (4)

4. Проверочное неравенство: для площади сечения среза можно записать

. (5)

5. Суммарная длина рабочих участков режущих кромок b будет равна

. (6)

6. Выражение для расчета угла схода стружки ₀ (при  =  = 0)

. (7)

С учетом же влияния углов   0 и   0 выражение для угла схода стружки, как было установлено Н.Н. Зоревым, имеет вид

. (8)

7. Расчет оптимальной по износостойкости инструмента

скорости резания v₀

С учетом использования принципа постоянства оптимальной температуры и на основе баланса тепловой и механической энергии в зоне резания для скорости v₀ было получено следующее выражение

, (9)

где k₁, k ₂ и k ₃ – аналитически определяемые безразмерные коэффициенты, учитывающие: k ₁ – механические и теплофизические свойства обрабатываемого и инструментального материалов; k ₂ – геометрические параметры инструмента; k ₃ – величину износа за период стойкости и глубину обрабатываемого отверстия; k _CОTС и k _ИП – коэффициенты, учитывающие, соответственно, влияние смазочно-охлаждающей среды и износостойкого инструментального покрытия (для определения к_СОТС была разработана экспериментальная методика экспресс-оценки).

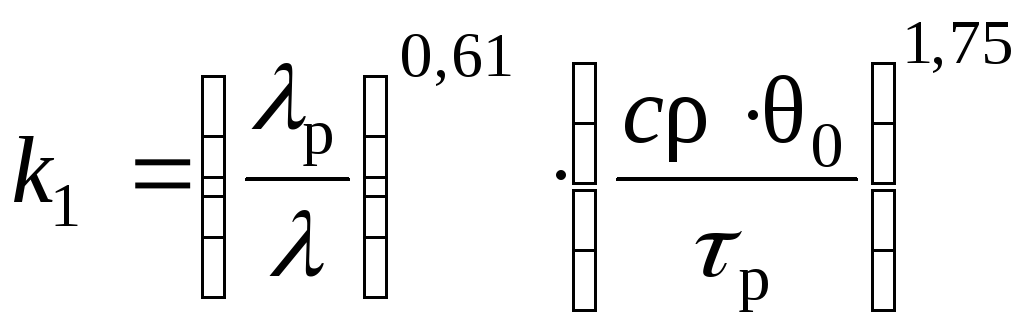; (10)

; (11)

при L ≤ 3d , (12)

где a = /c – коэффициент температуропроводности обрабатываемого материала, м²/с;  и _P – коэффициенты теплопроводности обрабатываемого и инструментального материалов, Вт/(мК); с – удельная объемная теплоемкость обрабатываемого материала, Дж/(м³К); τ_P – сопротивление обрабатываемого материала пластическому сдвигу, Па;  и  – среднеинтегральные значения переднего и заднего углов зуба инструмента,

рад;  и  – соответственно, углы заострения и при вершине зуба в плане, рад; ₁ – радиус округления режущей кромки, м; d – диаметр инструмента, м; _u – величина износа зуба инструмента по задней поверхности, м ( _u = h_з /2, здесь h_з – максимально допустимая величина износа по задней поверхности зуба зенкера, м); L – глубина отверстия, м.

Многочисленными исследованиями установлено, что при обработке отверстий глубиной L  3d на температуру резания начинает сказываться влияние вторичного теплообмена между стружкой, находящейся в отверстии, и инструментом, что приводит к необходимости корректировать скорость резания в сторону ее уменьшения.

В этом случае для расчета коэффициента k ₃ используется зависимость

. при L > 3d . (13)

8. Расчетное определение комплекса В = tg β₁

Для процесса зенкерования:

, (14)

где Ре = va₁/a; D = a₁/b₁; E = ₁/a₁; F = _P/ - безразмерные комплексы.