2.1.4. Резюме

Суммируя вышеизложенное, укажем, что числовые оценки приоритета судов на первоочередное обслуживание следует определять:

• на этапе составления СМГ – по формуле (2.4);

• на этапе реализации СМГ – по (2.10).

При этом наиболее выгодной (оптимальной) с точки зрения порта будет очередность обслуживания судов, сформированная по убыванию (невозрастанию), соответствующих соотношению в первом случае дохода порта, а во втором случае возможного прироста («размораживания») дохода порта в сумме со ставкой диспача (демереджа) к продолжительности грузовой обработки судов.

2.2. Распределение причалов между судами

2.3. Выбор технологии загрузки-разгрузки судов

2.4. Определение уровней концентрации технологических линий на судах

2.7. Определение расчетной продолжительности обслуживания судна

2.8. Месячное планирование обслуживания судов

2.9. Сменно-суточное планирование загрузки-разгрузки судов

2.5. Распределение технологических линий между судами

Пусть на интервале времени , разбитом на  отрезков (например, смен), планируется обработка s судов. При этом для каждого судна и каждой смены известны следующие величины: плановая загрузка k-го судна ; производительность одной перегру­зочной линии при обработке k-го судна ; количество технологических линий (ТЛ), которое можно использовать для обработки судов в -ю смену ; общий резерв машинного времени ТЛ в -ю смену ; предел концентрации ТЛ на k-м судне в -ю смену ; пре­дельная продолжительность обработки k-го судна в -ю смену эффективность одного машино-часа при обработке k-го судна в -ю смену , которая является приоритетной оценкой рассматриваемого судна.

Требуется составить план распределения ТЛ между судами по сменам такой при котором: будет обеспечена плановая загрузка (разгрузка) судов; в каждую смену будет использовано не более ТЛ; в каждую смену использования машинного времени ТЛ не превысит резерва ; суммарный эффект, обеспечиваемый в результате обработки судов будет наибольшим. Ряд авторов сводил эту задачу либо к «изящной», но не дающей конструктивного решения модели, либо к модели, достаточно адекватной реальному процессу, но совершенно «нерешабельной» вследствие отсутствия подходящих вычислительных методов. И лишь при записи этой задачи с использованием её неформальных свойств в терминах линейного программирования она реально поддается решению.

Положив , где - трудоемкость обработки судна, и , приходим к следующей модели:

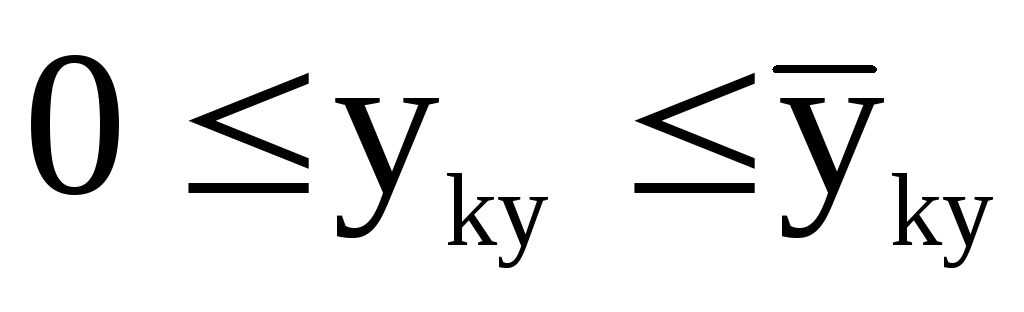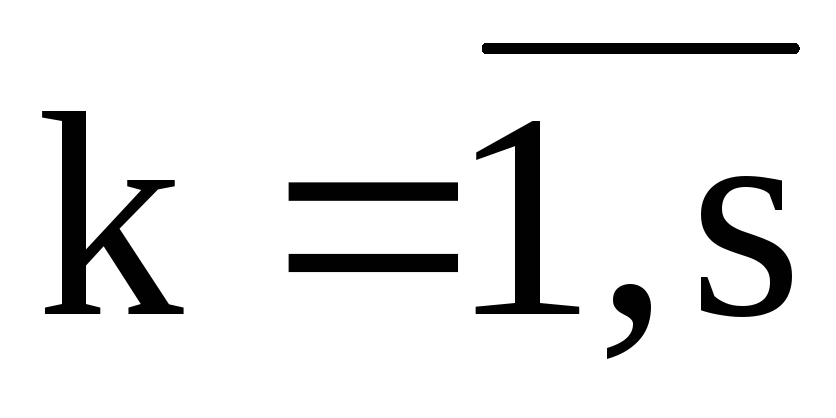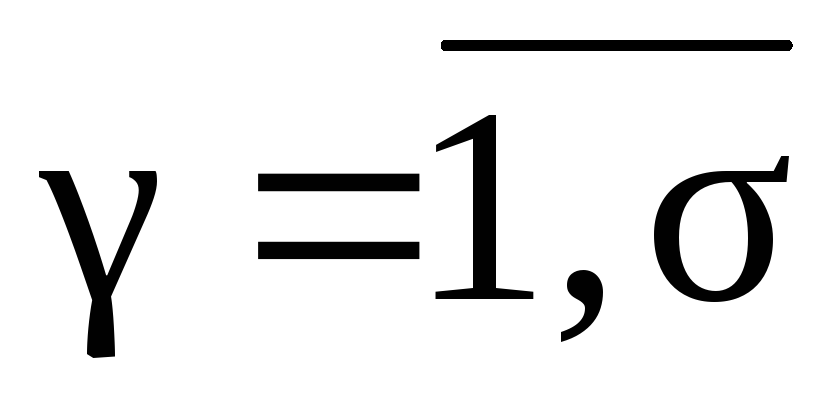,	, ;	(4)
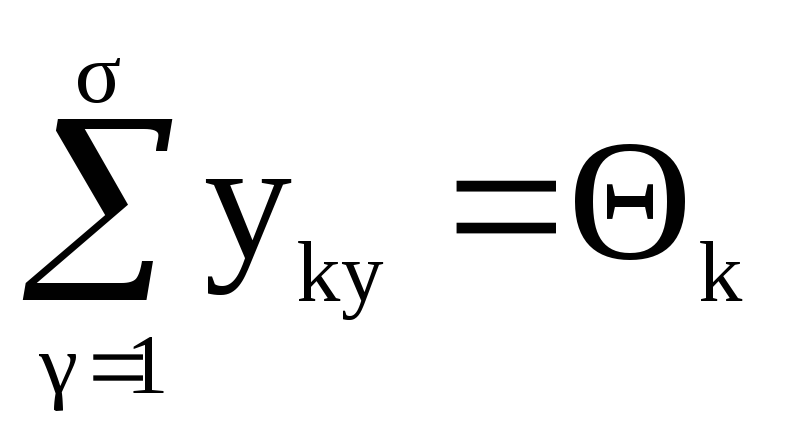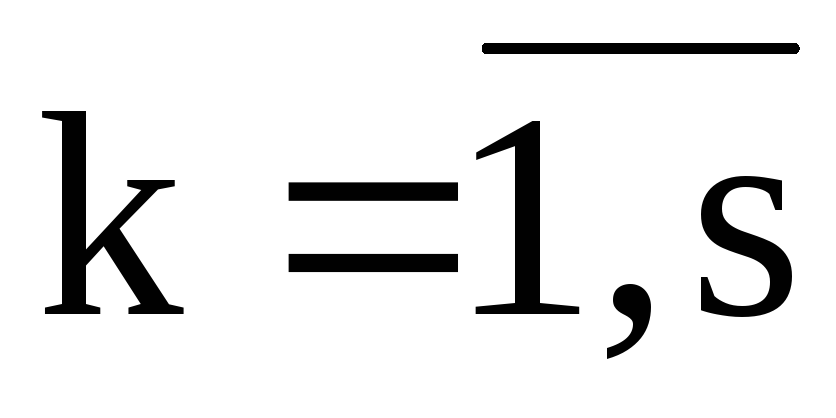,	;	(5)
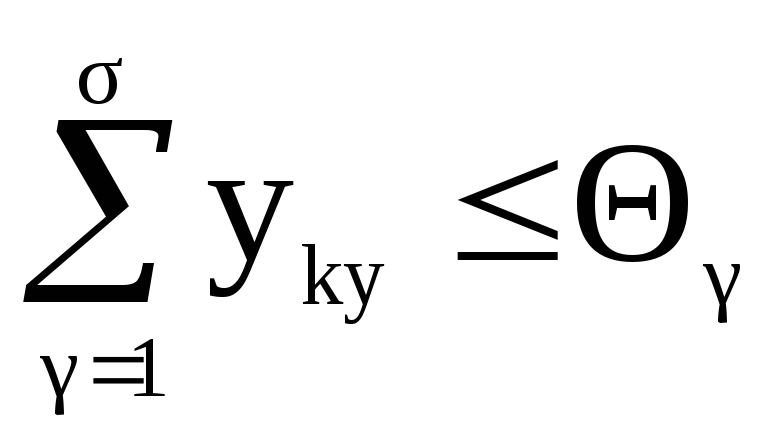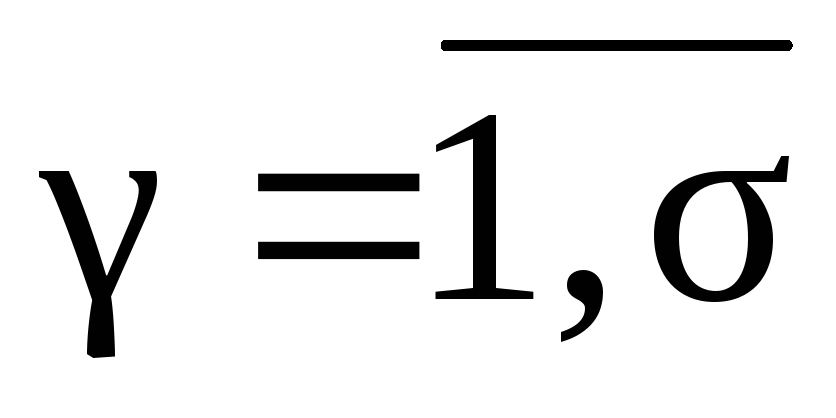,	;	(6)
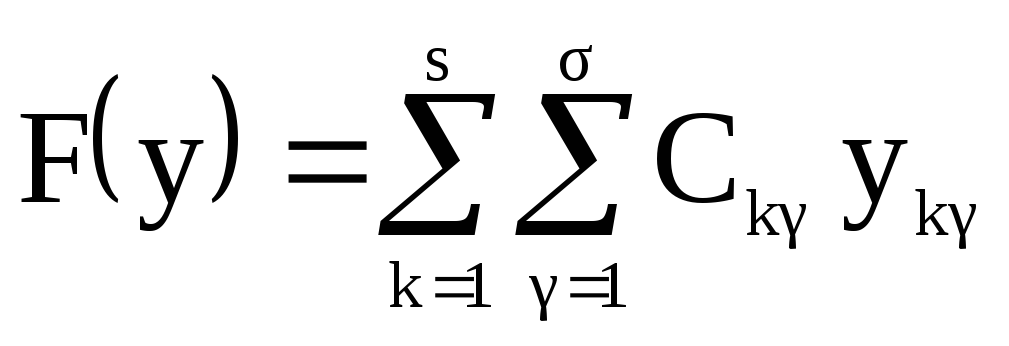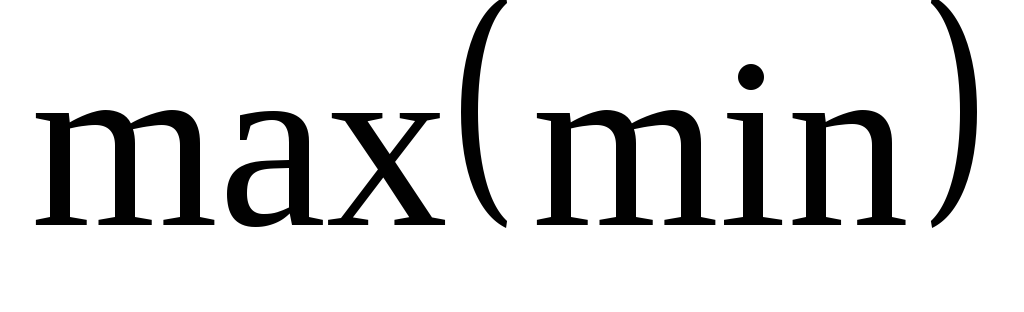- .		(7)

Таким образом, с формальной точки зрения задача о распределении ТЛ между судами состоит в максимизации (минимизации) функционала (7) при соблюдении условий (4)-(6).

В модели (4)-(7) используются оценки , которые являются условными и введены для того, чтобы можно было учесть ограничения на продолжительность обработки судов. Значения этих оценок задаются в соответствии с приоритетом судов на первоочередную обработку и дифференцируются в зависимости от совпадения (несовпадения) -й смены с календарными сроками обработки k-го судна.

На первый взгляд, модель (4)-(7) выглядит «простенькой», ибо относится к классу задач линейного программирования, которое критически воспринимается «рафинированными» теоретиками, отдающими предпочтение моделям целочисленного программирования. При этом, однако, сторонники последнего подхода старательно «обходят» проблему реализации целочисленной модели, а контрольные примеры решают симплекс-методом с последующим «ручным» обеспечением целочисленности переменных (параметров управления) модели. В нашем же случае необходимость в подобной «эквилибристике» отсутствует благодаря заданию дифференцированных значений коэффициентов при неизвестных в целевой функции, что, кстати сказать, также обеспечивает уникальность модели (4)-(7) и её решающее преимущество в сравнении со всеми другими моделями обсуждаемой задачи, опубликованными за последние 40 лет.