3. Кільця і поля

3.1. Означення кільця. Приклади кілець

Алгебраїчні структури , виступали в нас як найперші приклади моноїдів, причому на ми дивилися пізніше як на адитивну абелеву групу. Проте, у повсякденному житті ці структури найчастіше об'єднуються і виходить те, що в математиці називається кільцем. Важливий елемент елементарної арифметики полягає в дистрибутивному (або сполучному) законі , що здається тривіальним тільки через придбану звичку. Спробувавши, наприклад, об'єднати алгебраїчні структури , , де , ми вже не помітимо такої доброї узгодженості між двома бінарними операціями.

А зараз дамо точне означення кільця.

Означення. Непорожня множина , на якій визначені дві бінарні алгебраїчні операція + (додавання) і (множення), називається кільцем, якщо виконуються наступні умови (аксіоми кільця):

К1. – абелева група:

5. операція + асоціативна: ;

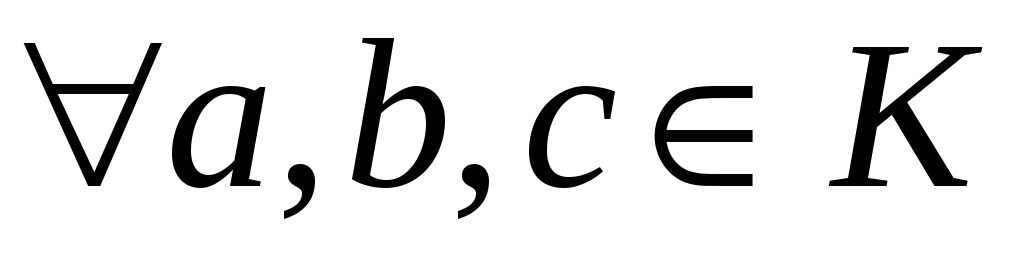
6. в множині існує нульовий елемент : ;

7. для кожного елемента існує протилежний елемент :

.

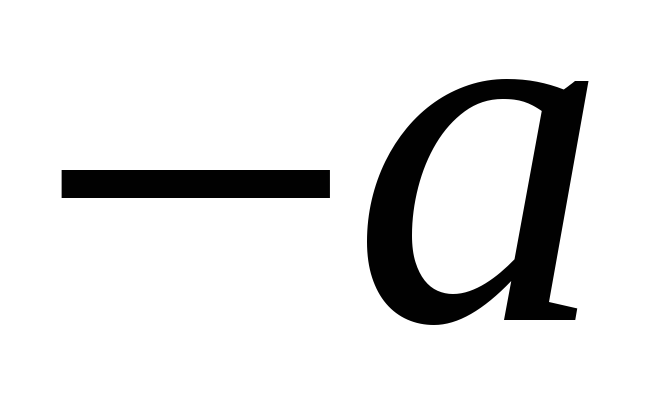8. операція + комутативна: .

К2. – півгрупа:

9. операція асоціативна: ;

К3. Операція (множення) дистрибутивна зліва і справа відносно операції+(додавання):

10. ;

;

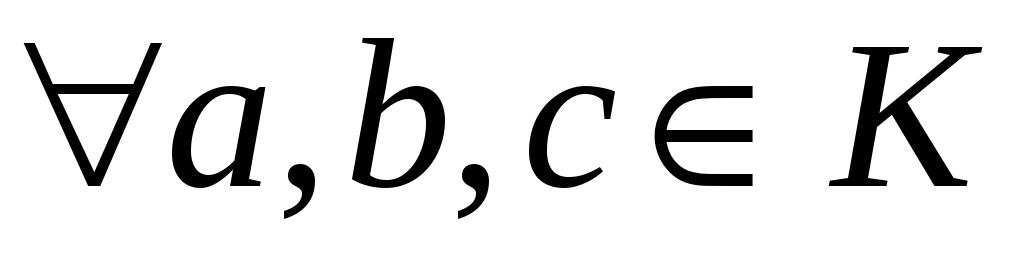
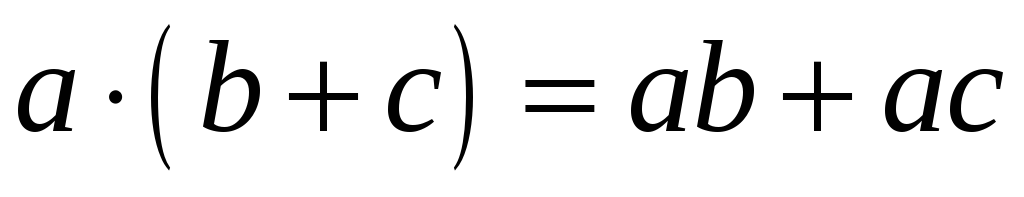Кільце позначається або просто .

Алгебраїчна структура називається адитивною групою кільця, а – його мультиплікативною півгрупою.

Означення. Кільце називається комутативним, якщо операція (множення) є комутативною, тобто

11. .

(На відміну від груп, комутативне кільце не прийнято називати абелевим).

Означення. Кільце називається кільцем з одиницею, якщо в існує одиничний елемент , відмінний від нульового, тобто

12. 

Інакше кажучи, – кільце з одиницею, якщо – моноїд.

Зауваження. В означенні кільця знаками + і позначено довільні операції, алгебраїчні на множині . Їх для зручності називають додаванням і множенням. Пам’ятаючи це, інколи операції вказувати не будемо, а будемо писати просто „кільце ”. Одиничний елемент позначають звичайним символом , хоча часто це не є число, а деякий інший математичний об’єкт.

Приклади.

1. – комутативне кільце цілих чисел з одиницею із звичайними операціями додавання і множення.

2. , , – комутативні кільця з одиницею.

Кільце, елементами якого є числа, називається числовим кільцем.

3. – некомутативне кільце з одиницею, яке називається кільцем квадратних матриць порядку з дійсними коефіцієнтами.

Можна розглядати кільце квадратних матриць над довільним комутативним кільцем , оскільки при додаванні і множенні двох матриць знову виходитиме матриця з коефіцієнтами з . Все це прямо витікає з формальних дій з матрицями.

Означення. Елемент називається оборотним елементом, якщо існує такий , що a.

Теорема. Множина всіх оборотних елементів кільця утворює групу по множенню, яка називається мультиплікативною групою кільця .

Приклад. 1. Мультиплікативною групою кільця цілих чисел є .

2. Мультиплікативною групою кільця є .

Багато властивостей кілець є переформулюваннями відповідних властивостей груп і взагалі – множин з однією асоціативною операцією. Інші властивості, більш специфічні для кілець і які випливають прямо з аксіом кільця, моделюють, по суті, властивості кільця . Відзначимо деякі з них:

1. В кожному кільці існує єдиний нульовий елемент, який називають нулем кільця.

2. В кожному кільці для будь-якого його елемента існує єдиний протилежний йому .

3. В кожному кільці сума елементів кільця не залежить від способу розстановки дужок, які вказують на послідовність виконання додавання цих елементів, і від порядку слідування доданків.

4. В кожному кільці рівні доданки в обох частинах рівності можна відкинути:

.

5. В кожному кільці для будь-якого його елемента і будь-якого справедлива рівність:

6. В кожному кільці містяться кратні , будь-якого його елемента .

Аналогічно моделюються і деякі інші властивості.

Наприклад,

В кожному кільці містяться цілі додатні степені будь-якого його елемента , причому

, .

Приклад. Довести, що множина всіх чисел виду , де , , є кільцем відносно звичайних операцій додавання і множення.

Доведення. Нехай і – два довільних елементи з множини . Тоді , , де . Маємо:

,

де , .

,

де , .

Оскільки , то і , тобто додавання і множення є алгебраїчними операціями на множині .

Аксіоми асоціативності, комутативності операцій додавання і множення, дистрибутивності множення відносно додавання виконуються на множині , оскільки виконуються для будь-яких комплексних чисел.

Нульовий елемент і одиничний елемент належать, очевидно, множині .

Якщо – довільне число з , то протилежне до нього число належить множині .

Таким чином, – комутативне кільце з одиницею. Його називають кільцем цілих гауссових чисел. □