2.7. Циклічні групи. Порядок елемента групи

Означення. Група, в якій всі елементи основної множини є степенями одного елемента , тобто є результатами k-кратного застосування операції (k=0,1,2,...), називається циклічною. Цей єдиний елемент називається твірним елементом циклічної групи. Циклічна група з твірним елементом позначається так: .

У відповідності до теореми про переріз підгруп і властивостей степенів у моноїдах природно очікувати, що будь-яка циклічна група з твірним елементом є абелевою групою вигляду або в залежності від того, яка група розглядається – мультиплікативна або адитивна. Насправді так воно і є, тільки треба ввести позначення і довести теорему:

Теорема (про властивості степенів). Які б не були

, .

(відповідно , )

Приклади.

1. Найпростішим прикладом циклічної групи є адитивна група цілих чисел , твірним якої є 1 або –1.

2. Множина є циклічною групою по множенню порядку 2.

3. Множина коренів -го степеня з 1 є циклічною групою по множенню.

4. Матриця породжує в групі нескінченну циклічну підгрупу.

Властивості циклічної групи

Теорема 1. Будь-яка підгрупа циклічної групи є циклічною.

Теорема 2. Для того, щоб елемент скінченної циклічної групи , , був твірним елементом цієї групи, необхідно і достатньо, щоб .

Нехай – довільна група, – деякий її елемент. Існують дві можливості:

1) Всі степені елемента різні, тобто (в адитивному записі ). В цьому випадку кажуть, що елемент має нескінченний порядок. Записують .

2) Є степені елемента збіжні, тобто при (в адитивному записі ). Якщо, наприклад, , то (в адитивному записі ). , тобто існують додатні степені елемента , які дорівнюють одиничному елементу. Нехай – найменший додатний показник, для якого (в адитивному записі ) . Тоді кажуть, що є елемент скінченного порядку . Записують .

В скінченній групі, ясно, всі елементи будуть скінченного порядку.

Теорема (про порядок елемента групи). Порядок будь-якого елемента довільної групи дорівнює порядку породженої ним циклічної групи:

.

Якщо – елемент скінченного порядку , то

і .

Приклад. Знайти порядки всіх елементів мультиплікативної групи

.

Розв’язання. Очевидно, що .

, , , . Отже, .

, . Отже, .

, , ,

. Отже, .

Таким чином, в циклічній групі існують два елементи, відмінні від одиничного, четвертого порядку, один – другого.

Приклад. Знайти порядки всіх елементів адитивної групи .

Розв’язання. Якщо , то , отже, .

Якщо , то, очевидно, не існує такого натурального числа , що . Отже, .

2.8 Групи підстановок

Нехай – скінченна множина з елементів. Оскільки природа цих елементів для нас неістотна, зручно вважати, що . Група всіх взаємно однозначних відображень називається симетричною групою -го степеня (інакше: симетричною групою на символах або на точках) і частіше позначається через . Її елементи, що зазвичай позначаються малими буквами грецького алфавіту, називаються підстановками. Тому і групу також називають ще групою підстановок.

У розгорненій і наочній формі підстановку , , зображають дворядним символом:

,

за допомогою двох перестановок, підписаних одна під одною, повністю вказуючи всі образи:

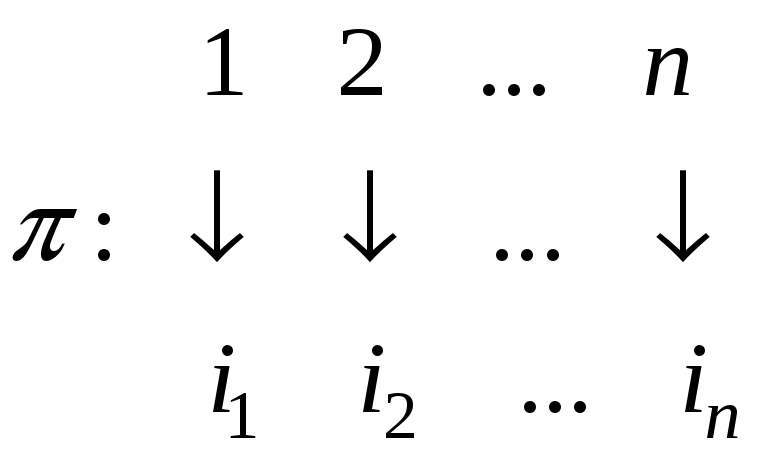
де , , – переставлені символи . Одинична (тотожна) підстановка: .

Підстановки перемножуються відповідно до загального правила композиції відображень: , тобто під множенням підстановок розуміють послідовне виконання відображень .

Приклад. Нехай

, .

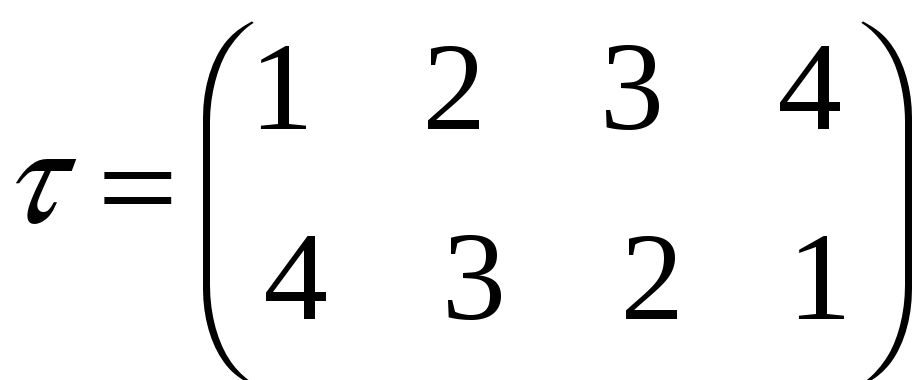Тоді

.

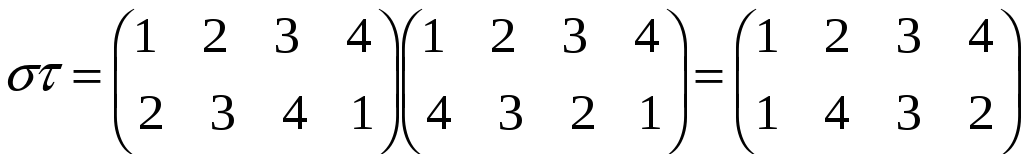В той же час

.

Отже .

Обернена підстановка може бути отримана з підстановки переставлення рядків в її записі:

.

Дійсно,

.

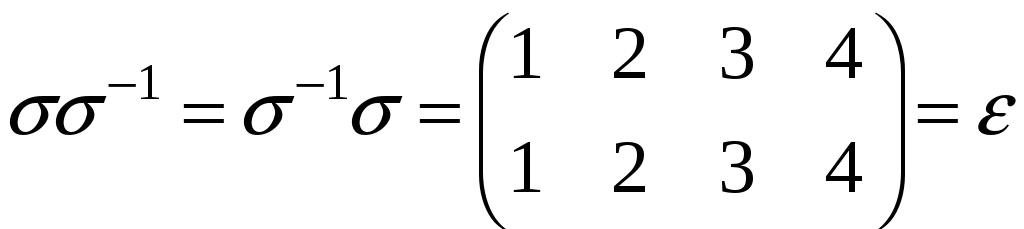Порядок групи підстановок дорівнює числу перестановок з елементів, тобто :

.

Будь-яка підстановка -го степеня може деякі з символів залишати на місці, інші ж дійсно переміщати.

Означення. Циклічною перестановкою або просто циклом називається підстановка така, що при повторенні її достатню кількість разів будь-який з символів, що дійсно переміщується, може бути переведений в будь-який інший з таких символів.

Приклад. Наступна підстановка 8-го степеня

дійсно переміщує символи 2,3,6 і 8, причому 2 переводить в 8, 8 переводить в 3, 3 – в 6, і 6 – знову в 2.

Цикли записуються так: символи, що дійсно переміщуються, записуються в круглих дужках один за одним в тому порядку, в якому вони один за одним переходять при повторенні підстановки. Для вказаного вище приклада цикл записується так: .

Означення. Довжиною циклу називається число символів, яке дійсно переміщується циклом.

Означення. Два цикли називаються незалежними, якщо вони не мають спільних символів, що дійсно переміщуються.

Зрозуміло, що при множенні незалежних циклів порядок множників не впливає на результат.

Будь-яка підстановка може бути єдиним способом розкладена в добуток попарно незалежних циклів.

Розклад на цикли є зручним способом запису підстановок.

Приклади.

;

.

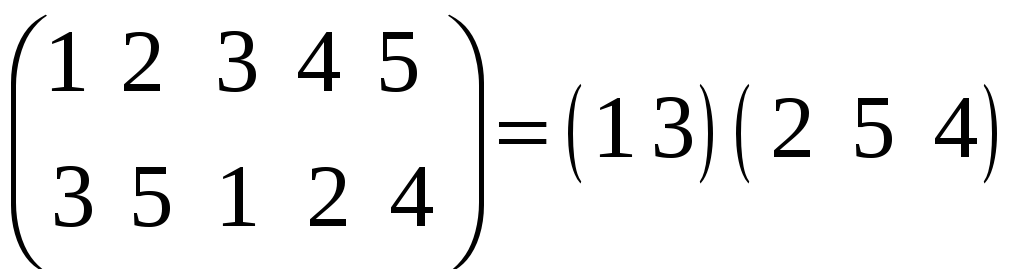Для будь-якої підстановки, що задана розкладом на цикли, можна знайти запис і в звичайній формі.

Приклад.

.

Означення. Цикл довжини 2 називається транспозицією.

Будь-яка транспозиція має вид і залишає на місці всі символи, відмінні від .

Для транспозицій справедлива наступна теорема.

Теорема. Будь-яка перестановка є добутком транспозицій. Цей розклад визначений однозначно з точністю до порядку слідування циклів.

Доведення. Насправді, будь-який цикл можна записати у вигляді добутку транспозицій таким чином:

. □

Приклад. У групі маємо: (1 2 3)=(1 3)(1 2)=(2 3)(1 3)=(1 3)(2 4)(1 2)(1 4).

Але треба відзначити, що ні про яку єдиність запису перестановки через транспозиції не може бути і мови. Транспозиції, взагалі кажучи, не комутують, а їх число не є інваріантом перестановки.

Означення. Нехай – перестановка символів . Кажуть, що в даній перестановці числа складають інверсію, якщо , але стоїть в цій перестановці раніше, ніж . Перестановка називається парною, якщо її символи складають парне число інверсій, і непарною –в протилежному випадку.

Теорема. Будь-яка транспозиція змінює парність перестановки.

Доведення. У випадку, коли символи , що переставляються, стоять поряд, то очевидно, що число інверсій змінюється на одиницю.

Нехай тепер між символами , що переставляються, розташовані символів, , тобто перестановка має вигляд

Транспозицію символів можна одержати в результаті послідовного виконання транспозицій сусідніх елементів. Таким чином, ми непарне число разів змінюємо парність перестановки, а тому одержимо перестановку, що має парність, протилежну початковій. □

Означення. Підстановка називається парною, якщо верхній і нижній її рядки мають однакову парність, як перестановки, і непарною в протилежному випадку.

Теорема. Нехай – підстановка з , – будь-який розклад в добуток трас позицій. Тоді число , яке називається знаком (або сигнатурою, або парністю ) цілком визначається підстановкою і не залежить від способу розкладу в добуток транспозицій.

Всі парні підстановки -го степеня утворюють підгрупу порядку , яка називається знакозмінною групою -го степеня.