5.2. Интерполяционный полином Эрмита

Перейдем теперь к задаче построения полинома Эрмита. Для этого, как и при определении разделенных разностей с кратными узлами, наряду с данными точками выберем на отрезке [a,b] точки . Все эти узлы различны. Построим по совокупности точек интерполяционный полином Ньютона с разделенными разностями

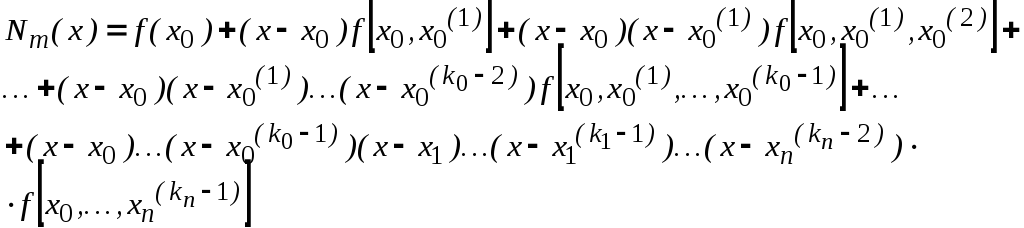Перейдем в обеих частях этого равенства к пределу при . Получим

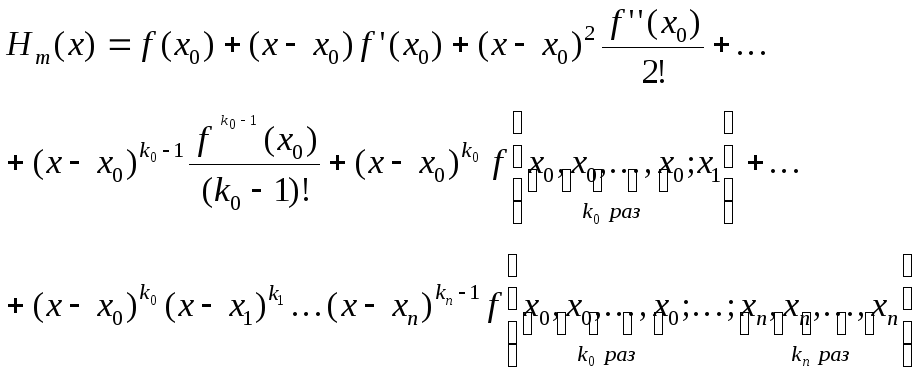(5.6)

Покажем, что полученный таким образом полином решает поставленную задачу, т.е. удовлетворяет условиям (5.2). Первые k₀ членов правой части (5.6) являются первыми k₀ членами разложения функции f(x) в ряд Тейлора. Остальные же члены содержат множитель . Поэтому выполняются условия (5.2), относящиеся к узлу x₀. Но мы могли бы записать , взяв за начальный узел не x₀, а любую из точек . При этом ни сам многочлен, ни его предел не изменятся, изменится только форма записи этих многочленов. Таким образом, условия (5.2) будут выполнены и для остальных узлов.

Остаточный член полинома Эрмита получится из остаточного члена полинома переходом к пределу при :

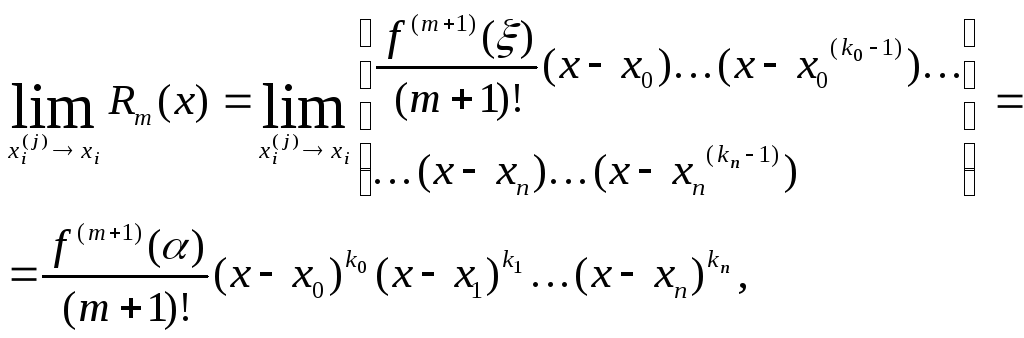
и остаточная погрешность определится как

Интерполяционный полином Эрмита можно получить другим способом. Наряду с рассмотрим интерполяционный полином Лагранжа , принимающий в точках значения . Разность должна быть многочленом степени не выше m, обращающимся в нуль в точках . Следовательно,

Где , а – многочлен степени (m-n-1). При любом функция

принимает в узлах интерполирования x_i значения f(x_i). Подберем теперь так, чтобы были выполнены и остальные условия (5.2). Дифференцируя последнее равенство, получим

.

Полагая здесь x = x_i, будем иметь

.

Так как , в каждой точке, в которой задана величина , мы найдем .

Дифференцируя еще раз, получим

Полагая снова x = x_i, найдем

Из этого равенства мы сумеем найти в тех точках, в которых заданы . Продолжим этот процесс далее. Каждый раз коэффициентом при старшей производной от в точках x_i будет . Таким образом, мы сведем нашу задачу отыскания к задаче отыскания , удовлетворяющего условиям:

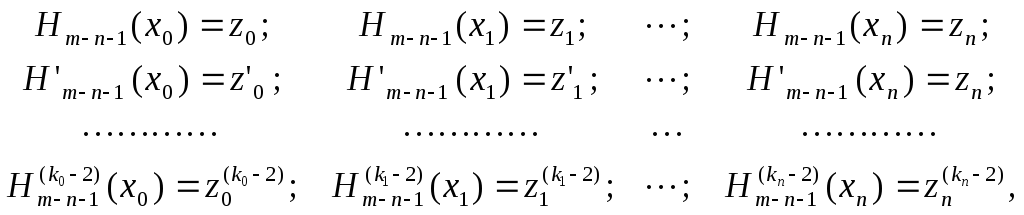
где , - известные числа. Для построения применим точно такой же прием. Получим некоторые условия, наложенные на , где . В конце концов, нам потребуется построить интерполяционный полином Лагранжа по его значениям в некоторых из точек x_i.

На практике полином Эрмита часто записывают в различных формах, которые определяются количеством заданных узлов и их кратностью. Например, полином Эрмита третьей степени, построенный по точкам , в которых заданы еще значения первой производной функции, можно записать в виде

, (5.7)

где – полиномы третьей степени, удовлетворяющие условиям:

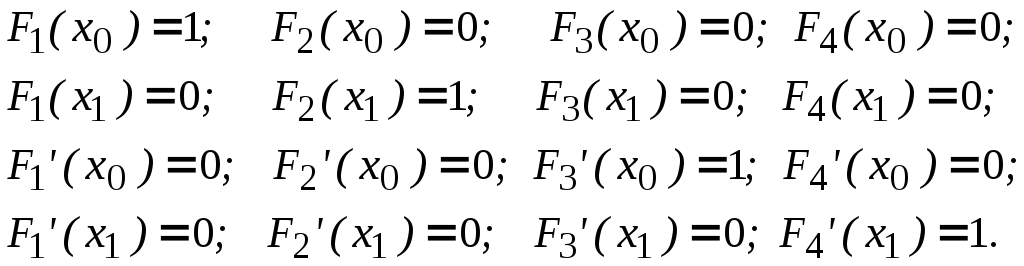(5.8)

Очевидно, что , определяемый формулой (5.7), удовлетворяет (5.2):

Иногда интерполяционный многочлен Эрмита строится методом неопределенных коэффициентов, т.е. рассматривается многочлен

и коэффициенты определяются из условий (5.2).

Вычислительная погрешность интерполяционного полинома Эрмита в точке x для каждой из его форм определяется так же, как и для интерполяционных полиномов Лагранжа, Ньютона и т.д. Например, для (5.7) вычислительная погрешность

Где – абсолютные погрешности величин соответственно.