За цикл операції середньоквадратичний момент

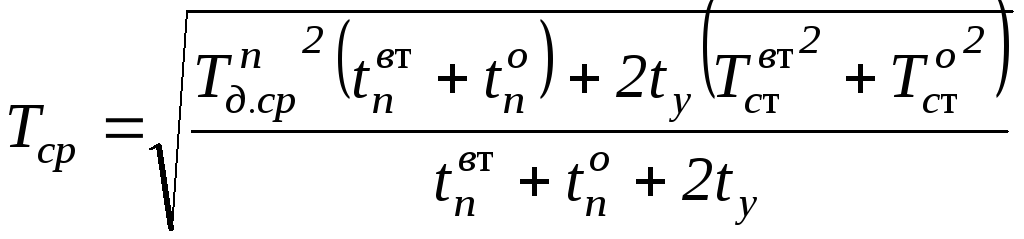. (9.48)

Умова, за якої двигун не перегріється:

.

9.5.3.3. Перевірка гальма на час гальмування механізму з вантажем

Перевірка здійснюється з метою визначення кута гальмування обертових частин і порівняння його з допустимою величиною.

Час гальмування

,

де – статичний момент при гальмуванні від нахилу площадки, натиску вітру та тертя в опорно-обертовому пристрої.

Має бути

,

де – допустимий час гальмування,

,

де – допустимий кут гальмування обертової частини крана.

9.6. Механізм зміни вильоту вантажу

9.6.1. Класифікація

Існують дві різні схеми механізмів зміни вильоту вантажу:

• із застосуванням вантажного візка (п. 9.4.3);

• із застосуванням стріли.

Схема із застосуванням вантажного візка являє собою механізм пересування візка з канатною тягою, вона була розглянута раніше.

Стрілові механізми змінюють виліт вантажу двома способами:

• зміною нахилу стріли;

• зміною довжини і нахилу стріли одноразово.

Зміна нахилу стріли може здійснюватись канатними, гідравлічними, рейковими та гвинтовими механізмами.

9.6.2. Стрілові механізми зміни вильоту вантажу нахилом стріли

На рис. 9.19 наведена схема механізму з канатним підйомом стріли.

Рис. 9.19. Розрахункова схема для визначення зусилля підйому стріли

Зусилля для підйому стріли F_стр визначаємо з рівняння моментів сил:

,

де G_вт – сила ваги вантажу;

G_стр – сила власної ваги стріли;

F_вт – зусилля в механізмі підйому вантажу.

Швидкість каната V_к, в якому діє зусилля F_стр, визначаємо через швидкість зміни вильоту вантажу V_вил. За один і той самий час t виліт змінюється на величину , а відрізок Х – на величину , тобто

.

Кут нахилу стріли при зміні вильоту вантажу змінюється в межах . Залежно від цього змінюються плечі діючих на стрілу сил, а значить – зусилля F_стр і швидкість V_к.

Розрахункова потужність

(9.49)

також змінюється в межах при підніманні стріли. Потрібна потужність двигуна в цьому випадку може бути визначеною як середньоквадратична за один підйом стріли, тобто

Аналогічні розрахунки повинні бути виконані для знаходження найбільшого зусилля гальмування стріли. Потрібний гальмовий момент

,

де – найбільший момент гальмування стріли;

– коефіцієнт запасу гальмування, який за величиною приймається так, як для механізму підйому вантажу.

Стрілові крани часто проектуються як крани-екскаватори. У таких моделях кранів стріли виготовляються більш жорсткими і мають змінну довжину. Як і стрілові широко розповсюджуються крани з телескопічними стрілами.

РОЗДІЛ 10

НАВАНТАЖЕННЯ КРАНОВИХ КОНСТРУКЦІЙ ПРИ РОЗРАХУНКУ ДЕТАЛЕЙ НА СТАТИЧНУ І ЦИКЛІЧНУ МІЦНОСТІ

10.1. Комбінації зовнішніх навантажень на вантажопідйомну машину для розрахунку деталей на статичну і циклічну міцності

При розрахунку конструкцій вантажопідйомних машин на міцність застосовують три комбінації зовнішніх навантажень:

1. номінальні навантаження робочого стану машини;

2. найбільші навантаження робочого стану машини;

3. найбільші навантаження неробочого стану машини.

Першу комбінацію навантажень при розрахунку вантажопідйомних кранів становлять:

– вага вантажу, що не перевищує номінальну масу;

– середня власна вага крана;

– середні навантаження від нахилу площадки або колії;

– середні навантаження вітряного натиску робочого стану крана;

– середні інерційні навантаження.

Другу комбінацію навантажень становлять:

– найбільші можливі при роботі крана навантаження на робочому органі;

– найбільші зусилля від нахилу площадки чи колії;

– найбільші інерційні навантаження при роботі крана з урахуванням пружних коливань конструкції;

– найбільші навантаження вітряного напору робочого стану крана.

Третю комбінацію навантажень становлять:

– найбільший вітряний натиск на конструкції крана неробочого стану з урахуванням динамічних навантажень від поривів вітру;

– найбільший можливий за нормативом нахил площадки.

Статична міцність деталі є опір її матеріалу руйнуванню від найбільшого одноразово діючого зусилля. При розрахунку статичної міцності деталей вантажопідйомних кранів застосовують другу і третю комбінації зовнішніх навантажень. При цьому загальна модель розрахунку має вигляд:

,

де – напруження (нормальні чи дотичні) найбільшої можливої величини;

Ω – зведені навантаження другої або третьої комбінацій до перерізу деталі;

Θ – геометричні параметри опору перерізу;

ξ – сумарний коефіцієнт запасу статичної міцності деталі;

– допустимі нормальні (чи дотичні) напруження для матеріалу деталі, які визначаються його фізико-механічними характеристиками – межою текучості та межою міцності.

Циклічна міцність деталі є опір її матеріалу руйнуванню втомою. Втому викликають не найбільші, а середні за величиною, не одноразово діючі навантаження. При розрахунку циклічної міцності кранів застосовують першу комбінацію навантажень, коли навантаження діють у великій кількості продовж повного терміну роботи крана. При цьому загальна модель розрахунку має вигляд:

,

де – еквівалентні напруження, дія яких на матеріал перерізу призводить його до того ж стану втоми, як деяка кількість окремих напружень різної величини;

Ω_Е – еквівалентні навантаження першої комбінації;

ξ_Е – коефіцієнт запасу циклічної міцності деталі;

– межа витривалості матеріалу;

r – коефіцієнт асиметрії циклу напружень;

k – коефіцієнт концентрації напружень у перерізі.

Таким чином, при розрахунках статичної міцності деталей крана використовують комбінації зовнішніх навантажень найбільшої величини – найбільші робочого та неробочого станів крана; при розрахунках циклічної міцності використовують комбінацію найчастіше діючих навантажень – номінальних навантажень робочого стану крана.

10.2. Найбільші інерційні навантаження на конструкції крана з урахуванням пружних коливань

У реальних умовах сталеві вироби не абсолютно жорсткі, а мають кінцеву жорсткість. У результаті при несталих рухах виникають пружні коливання як у самих деталях, так і в їх з’єднаннях. Амплітудні значення зусиль при коливаннях перевищують звичайні інерційні навантаження абсолютно жорстких тіл. Для більш точних розрахунків статичної міцності деталей враховують найбільші зусилля, які називають динамічними.

Найбільші динамічні навантаження в механізмі підйому вантажу виникають під час пуску механізму з вантажем. Розглянемо два можливі розрахункові випадки:

– піднімання вантажу «з ваги», коли пуск механізму здійснюється з попередньо піднятим вантажем, і підйомні канати, навантажені його вагою;

– піднімання вантажу «з підхопленням», коли пуск механізму здійснюється з положення вантажу на основі, і підйомні канати послаблені.

Підніманні вантажу «з ваги»

Механізм підйому вантажу (рис. 10.1) можна розглядати як багатомасову систему з масами m_в1 , m_в2, m_в3, ..., з’єднаними між собою пружними елементами з жорсткістю с_в1 , с_в2, с_в3, ... Останній вал через барабан з’єднаний з масою вантажу Q пружним елементом у вигляді канатного поліспаста з жорсткістю с_пол.

Багатомасову систему механізму зводимо до двомасової (див. рис.10.1):

m₁ – маса всієї привідної частини механізму;

m₂ – маса вантажу з вантажним захоплювачем (далі – маса вантажу).

Першим кроком в розрахунках двомасової динамічної системи визначають зведені маси m₁ і m₂ і зведену жорсткість С з’єднання цих мас.

Визначення зведених мас m₁ і m₂

Лінію зведення для мас m₁ і m₂ і жорсткості С можна призначити на різній ділянці кінематичної схеми механізму. Для механізму підйому вантажу за схемою рис. 10.1 найбільш доцільним є розміщення лінії зведення на осі гілки каната, яка збігає з поліспаста на барабан.

Рис. 10.1. Перетворення багатомасової системи механізму підйому вантажу на двомасову

Масу m₁ привідних (обертових) частин механізму визначимо, користуючись відомим з попередніх розрахунків механізмів моментом інерції обертових частин І_об. Зведений до вала барабана момент інерції привідних частин:

Тоді умовна маса привідних частин механізму, що розташована на твірній обичайки барабана:

.

Масу m вантажу визначимо, користуючись рівнянням кінетичних енергій

,

де V– швидкість каната, що виходить на барабан з поліспаста,

Тоді

m= Q; m=. (10.1)

Визначення зведеної жорсткості С

При визначенні зведеної жорсткості С умовного пружного елемента користуємось відомими залежностями.

Лінійна деформація стрижня за законом Гука

;

= С,

де С – лінійна жорсткість стрижня площею перерізу А, довжиною і модулем пружності матеріалу Е;

Аналогічно кутова деформація стрижня при крученні

,

де C – крутна жорсткість стрижня з моментом інерції перерізу ;

= C.

Звідси маємо залежності:

C= ; C=; =; =; =;

(10.2)

=.

Для визначення зведеної жорсткості С розглянемо деформацію привідної частини механізму з крутною жорсткістю C і деформацію поліспаста з лінійною жорсткістю С (рис. 10.2), використовуючи формули (10.2).

Рис. 10.2. Зведення крутної жорсткості привідної частини механізму і лінійної жорсткості поліспаста до лінії зведення

Жорсткість С за рис. 10.1 будемо визначати як

С =, (10.3)

де – зусилля в гілці каната, що набігає на барабан;

– дуга на твірній барабана, яка відповідає сумарному куту повороту барабана,

= +, (10.4)

де – кут повороту барабана від пружності привідної частини,

=,

де – крутний момент на барабані;

– кут повороту барабана від пружності каната в поліспасті,

=,

де – дуга, довжина якої дорівнює лінійній деформації каната в поліспасті,

=; =.

Підставимо значення величин в (10.4):

=+ або = + ,

тобто =.

Підставивши в (10.3) значення як =,

тобто =,

маємо С =.

Формула може бути переписана у вигляді

С = .

Визначення величини зусилля в кінематичному ланцюгу механізму під час пуску

Динамічна система за рис. 10.1 під час пуску навантажена зовнішніми зусиллями:

Р – пускове зусилля від двигуна, прикладене до маси m₁;

G – сила ваги, що прикладена до вантажу при його підніманні «з ваги» .

Під впливом сили Р маса m₁ першою починає рухатися, маса m₂ ще деякий час залишається у спокої за рахунок пружної деформації системи, а потім переміщується в тому ж напрямку. Таким чином, після одного і того самого проміжку часу маса m₁ пройде шлях X₁, маса m₂ пройде шлях X_2.. Пружний елемент здеформується на величину ∆ = X₁ – X₂ , і в ньому виникне внутрішня сила F = С∆, тобто

F = С(X₁ – X₂ ). (10.5)

У цей час на маси діють сили:

на масу m₁ – пускове зусилля P, сила інерції , сила з боку пружного елемента F;

на масу m₂ – сила ваги вантажу G, сила інерції , сила з боку пружного елемента F.

Рівняння рівноваги кожної маси при дії прикладених сил мають вигляд:

=;

=.

З цих рівнянь маємо:

= ; (10.6)

=. (10.7)

До рівнянь (10.6) і (10.7) входять постійні величини P, G та маси m₁ і m₂. Змінними є переміщення X₁ і X₂, а також сила F, яка залежить від цих переміщень за формулою (10.5). Візьмемо другу похідну від виразу (10.5):

=-.

Підставимо значення та з (10.6) і (10.7).

Маємо =,

або =;

=;

=. (10.8)

Диференційне рівняння (10.8) описує процес пружних коливань у механізмі під час його пуску. Змінною величиною в цьому рівнянні є внутрішня динамічна сила F, яка передається через ланки кінематичної схеми механізму, тобто через його деталі. Задача полягає в тому, щоб визначити найбільше значення цієї сили F.

Загальне рішення рівняння (10.8) є

F= A cos ωt + B sin ωt + D, (10.9)

де ω – кутова швидкість,

;

D – окреме рішення, при чому

,

де права сторона рівняння є вільним членом у виразі (10.8). Тоді

;

;

;

. (10.10)

При визначенні постійних А і B в (10.9), виходимо з наступних міркувань.

При t=0 F=G, тому що підвішений вантаж створює у всіх ланках кінематичної схеми механізму адекватне G зусилля. Тоді, підставивши в рівняння (10.9) t=0 і значення D з (10.10), маємо:

; ;

. (10.11)

При визначенні B враховуємо, що коли t=0 і F=G, перша похідна ==0.

Візьмемо першу похідну з рівняння (10.9):

=(-.

При =0 і t=0 , і оскільки , то B=0.

Значення A, B і D підставляємо в (10.9):

. (10.12)

Найбільше амплітудне значення змінної F настає на півперіоді синусоїди коливань, тобто при , де період коливань,

.

Підставимо значення в (10.12). Тоді пошукове найбільше зусилля

.

Підставивши , маємо

. (10.13)

Можна виразити величини, що входять до формули (10.13), через номінальне зусилля ваги вантажу і деякий коефіцієнт, який збільшує найбільше зусилля в системі над номінальним:

.

Коефіцієнт називають коефіцієнтом динаміки системи. Якщо пускове зусилля системи записати як

,

де – коефіцієнт збільшення пускового зусилля двигуна над номінальним,

то =,

або . (10.14)

З останнього виразу виходить, що при певному співвідношенні між масами m₁ і m₂ коефіцієнт динаміки переважає коефіцієнт .

Підніманні вантажу «з підхопленням»