
Пакет №14
Разложите вектор
![]() по векторам
по векторам
![]() и
и
![]() .
.
1)![]() ,
,
![]() ={2;
-1},
={2;
-1}, ![]() ={3;
2};
={3;
2};
2)![]() ,
,
![]() ={1;
1},
={1;
1}, ![]() ={2;
-1};
={2;
-1};
3)![]() ,
,
![]() ={1;
-1},
={1;
-1}, ![]() ={2;
3};
={2;
3};
4)![]() ,
,
![]() ={2;
1},
={2;
1}, ![]() ={-3;
5};
={-3;
5};
5)![]() ,
,
![]() ={2;
2},
={2;
2}, ![]() ={-4;
-2};
={-4;
-2};
6)![]() ,
,
![]() ={2;
3},
={2;
3}, ![]() ={-1;
2};
={-1;
2};
7)![]() ,
,
![]() ={1;
2},
={1;
2}, ![]() ={2;
-1};
={2;
-1};
8)![]() ,
,
![]() ={5;
3},
={5;
3}, ![]() ={8;
-2};
={8;
-2};
9)![]() ,
,
![]() ={2;
1},
={2;
1}, ![]() ={-3;
4};
={-3;
4};
10)![]() ,
,
![]() ={2;
-1},
={2;
-1}, ![]() ={2;
1}.
={2;
1}.
Пакет №15
Даны векторы
![]() ={ax;
ay;
az}
и
={ax;
ay;
az}
и
![]() ={bx;
by;
bz}.
Найдите косинус угла между векторами
={bx;
by;
bz}.
Найдите косинус угла между векторами
![]() и
и
![]()
1)
![]() ={2;
-1; 1},
={2;
-1; 1},
![]() ={3;
2; -1}; 6)
={3;
2; -1}; 6)
![]() ={2;
3;1},
={2;
3;1},
![]() ={-1;
2; -2};
={-1;
2; -2};
2)
![]() ={1;
1; 3},
={1;
1; 3},
![]() ={2;
-1; 2}; 7)
={2;
-1; 2}; 7)
![]() ={1;
2; 1},
={1;
2; 1},
![]() ={2;
-1; 3};
={2;
-1; 3};
3)
![]() ={1;
-1; 2},
={1;
-1; 2},
![]() ={2;
3; -2}; 8)
={2;
3; -2}; 8)
![]() ={5;
3; 2},
={5;
3; 2},
![]() ={8;
-2; 1};
={8;
-2; 1};
4)
![]() ={2;
1; 4},
={2;
1; 4},
![]() ={-3;
5; 1}; 9)
={-3;
5; 1}; 9)
![]() ={2;
1; 1},
={2;
1; 1},
![]() ={-3;
4; -4};
={-3;
4; -4};
5)
![]() ={2;
1; 3},
={2;
1; 3},
![]() ={-4;
-2; -1}; 10)
={-4;
-2; -1}; 10)
![]() ={2;
-1; 1},
={2;
-1; 1},
![]() ={2;
1; 1}.
={2;
1; 1}.
Пакет № 16
Заданы координаты вершин треугольника АВС. Составить уравнения медианы и высоты треугольника, проведенных через вершину В:
![]()
![]()
![]()
![]()
![]()
Пакет № 17
Заданное уравнение привести к каноническому виду и построить в плоскости Оху соответствующую кривую:
1)
![]() ;
6)
;
6)
![]()
2)
![]() ;
7)
;
7)
![]() ;
;
3)
![]() ;
8)
;
8)
![]() ;
;
4)
![]() ;
9)
;
9)
![]() ;
;
5)
![]() ;
10)
;
10)
![]() .
.
Пакет № 18
Составить уравнение плоскости, проходящей через точку
М (![]() )
перпендикулярно вектору
)
перпендикулярно вектору
![]() ,
если
,
если
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пакет № 19
Составить
канонические уравнения прямой, проходящей
через точку
![]() параллельно вектору
параллельно вектору
![]() :
:
1) М (-1; 2; 4);
![]() ;
6) М (-2; 3; 1);
;
6) М (-2; 3; 1);
![]() ;
;
2) М (2; -1; 5);
![]() ;
7) М (-5; 2; -3);
;
7) М (-5; 2; -3);
![]() ;
;
3) М (4; -2; -1);
![]() ;
8) М (4; -2; 0);
;
8) М (4; -2; 0);
![]() ;
;
4) М (7; 1; -1);
![]() ;
9) М (7; 0; -3);
;
9) М (7; 0; -3);
![]() ;
;
5) М (-4; -2; 0);
![]() ;
10) М (-1; 3; 1);
;
10) М (-1; 3; 1);
![]() .
.
Пакет № 20
Найти точку
пересечения прямой
 и плоскости
и плоскости
![]() :
:
1)
 ;
;
![]() ;
;
![]() 6)
6) ;
;
![]()
2)
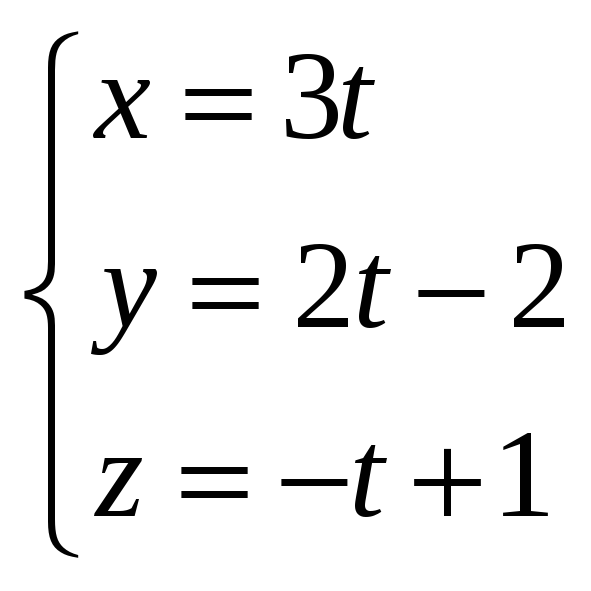 ;
;
![]() ;
7)
;
7)
 ;
;
![]() ;
;
3)
 ;
;
![]() ;
8)
;
8)
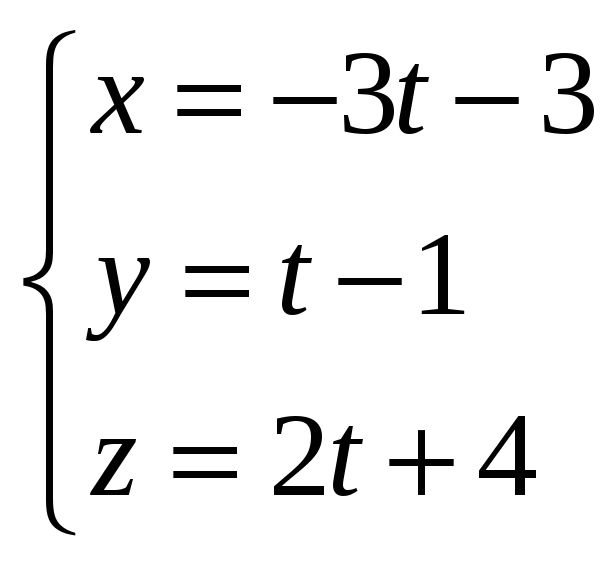 ;
;
![]() ;
4)
;
4)
 ;
;
![]() ;
9)
;
9)
 ;
;
![]() ;
;
5)
 ;
;
![]() ;
10)
;
10)
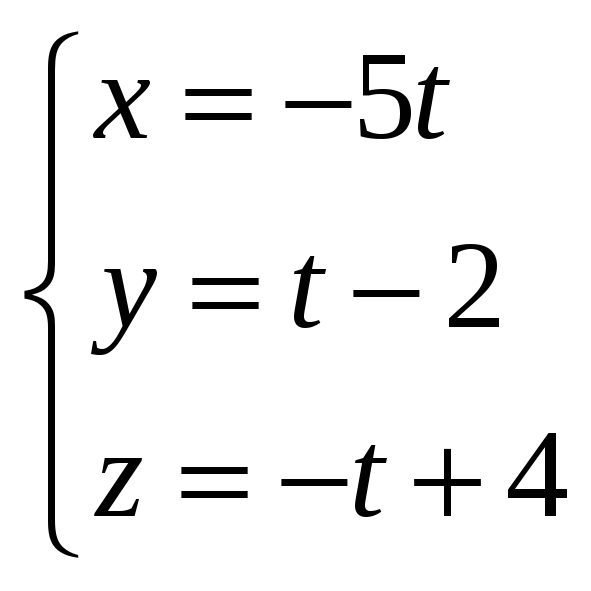 ;
;
![]() ;
;
Пакет № 21.
Найти частные
производные функции
![]() .
.
1)
![]() ;
2)
;
2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() .
.
Пакет № 22.
Написать уравнение
касательной плоскости к поверхности
![]() в точке
в точке
![]() .
.
1)
![]() ;
;
![]() ; 6)
; 6)
![]() ;
;
![]() ;
;
2)
![]() ;
;
![]() ; 7)
; 7)
![]() ;
;
![]() ;
;
3)
![]() ;
;
![]() ; 8)
; 8)
![]() ;
;
![]() ;
;
4)
![]() ;
;
![]() ; 9)
; 9)
![]() ;
;
![]() ;
;
5)
![]() ;
;
![]() ; 10)
; 10)
![]() ;
;
![]() .
.
Пакет № 23.
Найти градиент
функции
![]() в точке
в точке
![]() и его модуль.
и его модуль.
1)
![]() ;
;
![]() ; 6)
; 6)
![]() ;
;
![]() ;
;
2)
![]() ;
;
![]() ; 7)
; 7)
![]() ;
;
![]() ;
;
3)
![]() ;
;
![]() ; 8)
; 8)
![]() ;
;
![]() ;
;
4)
![]() ;
;
![]() ; 9)
; 9)
![]() ;
;
![]() ;
;
5)
![]() ;
;
![]() ; 10)
; 10)
![]() ;
;
![]() .
.
Пакет № 24.
Найти критические точки и исследовать на экстремум функцию z=f (x,y).
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ; 10)
; 10)
![]() .
.
Пакет № 25.
Фирма производит товар двух видов в количествах x и y. Задана функция полных издержек C(x,y). Цены этих товаров на рынке равны P1 и P2. Определить, при каких объемах выпуска достигается максимальная прибыль, найти эту прибыль.
1)
![]() ;
P1=
48; P2=
58;
;
P1=
48; P2=
58;
2)
![]() ;
P1=
42; P2=
44;
;
P1=
42; P2=
44;
3)
![]() ;
P1=
110; P2=
70;
;
P1=
110; P2=
70;
4)
![]() ;
P1=
42; P2=
48;
;
P1=
42; P2=
48;
5)
![]() ;
P1=
98; P2=
130;
;
P1=
98; P2=
130;
6)
![]() ;
P1=
36; P2=
32;
;
P1=
36; P2=
32;
7)
![]() ;
P1=
26; P2=
16;
;
P1=
26; P2=
16;
8)
![]() ;
P1=
64; P2=
70;
;
P1=
64; P2=
70;
9)
![]() ;
P1=
32; P2=
18;
;
P1=
32; P2=
18;
10)
![]() ;
P1=
52; P2=
64.
;
P1=
52; P2=
64.
Пакет № 26.
Фирма производит товар двух видов в количествах x и y. Функция полных издержек определена соотношением C= C(x, y). Цены этих товаров на рынке равны P1(x) и P2(y). Определить, при каких объемах выпуска достигается максимальная прибыль на множестве производственных возможностей, ограниченном издержками производства в объеме C= C0. Найти эту прибыль.
1)
![]() ;
P1(x)=
21 – x;
P2(y)=
62 – 2y;
C0=
175;
;
P1(x)=
21 – x;
P2(y)=
62 – 2y;
C0=
175;
2)
![]() ; P1(x)=
25 – x;
P2(y)=
35 – y;
C0=
100;
; P1(x)=
25 – x;
P2(y)=
35 – y;
C0=
100;
3)
![]() ;
P1(x)=
20 – x;
P2(y)=
24 – y;
C0=
74;
;
P1(x)=
20 – x;
P2(y)=
24 – y;
C0=
74;
4)
![]() ;
P1(x)=
60 – 2x;
P2(y)=
80 – 2y;
C0=
180;
;
P1(x)=
60 – 2x;
P2(y)=
80 – 2y;
C0=
180;
5)
![]() ;
P1(x)=
23 – x;
P2(y)=
42 – 2y;
C0=
228;
;
P1(x)=
23 – x;
P2(y)=
42 – 2y;
C0=
228;
6)
![]() ;
P1(x)=
25 – x;
P2(y)=
35 – y;
C0=
180;
;
P1(x)=
25 – x;
P2(y)=
35 – y;
C0=
180;
7)
![]() ;
P1(x)=
48 – x;
P2(y)=
36 – y;
C0=
180;
;
P1(x)=
48 – x;
P2(y)=
36 – y;
C0=
180;
8)
![]() ;
P1(x)=
10 – 0,5x;
P2(y)=
15 – 0,5y;
C0=
30,5;
;
P1(x)=
10 – 0,5x;
P2(y)=
15 – 0,5y;
C0=
30,5;
9)
![]() ;
P1(x)=
62 –
2x;
P2(y)=
21 – y;
C0=
165;
;
P1(x)=
62 –
2x;
P2(y)=
21 – y;
C0=
165;
10)
![]() ;
P1(x)=
126 – 3x;
P2(y)=
63 – 2y;
C0=
516.
;
P1(x)=
126 – 3x;
P2(y)=
63 – 2y;
C0=
516.
Пакет № 27
Найдите следующие неопределенные интегралы
1) а)
![]() б)
б)
![]() 2) а)
2) а)
![]() б)
б)
![]()
3) а)![]() б)
б)![]() 4) а)
4) а)![]() б)
б)![]()
5) а)
![]() б)
б)
![]() 6) а)
6) а)![]() б)
б)![]()
7) а)![]() б)
б)![]() 8) а)
8) а)![]() б)
б)![]()
9) а)![]() б)
б)![]() 10) а)
10) а)
![]() б)
б)![]()
Пакет № 28
Найти неопределенные интегралы:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]()
Пакет № 29
Найти неопределенные интегралы (применяя формулы интегрирования по частям)
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]() 7)
7)
![]()
8)
![]() 9)
9)
![]() 10)
10)
![]()
Пакет № 30
Вычислить определенные интегралы
1)
![]() 2)
2)
![]() 3)
3)
 4)
4)
![]()
5)
![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
Пакет № 31
Изобразить область, ограниченную графиками заданных функций и найти её площадь
1)
![]() ;
;
![]() ;
;
![]() ;
;
![]() 2)
2)
![]() ;
;
![]() ;
;
![]()
3)
![]() ;
;
![]() 4)
4)
![]() ;
;
![]()
5)
![]() ;
;
![]() 6)
6)
![]() ;
;
![]()
7)
![]() ;
;
![]() 8)
8)
![]() ;
;
![]()
9)
![]() ;
;
![]() 10)
10)
![]() ;
;
![]()
Пакет № 32
Вычислить несобственные интегралы или доказать их расходимость
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
Пакет № 33.
Исследовать ряд на сходимость.
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
9)
;
9)![]() ; 10)
; 10)![]() .
.
Пакет № 34.
Исследовать ряд на сходимость, используя признак Даламбера.
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
;
9)![]() ;
10)
;
10)![]() .
.
Пакет № 35.
Решить уравнение
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
Пакет № 36.
Найти частное решение уравнения, удовлетворяющее заданному начальному условию.
1)
![]() ;
;
![]() 2)
2)
![]() ;
;
![]()
3)
![]() ;
;
![]() 4)
4)
![]() ;
;
![]()
5)
![]() ;
;
![]() 6)
6)
![]() ;
;
![]()
7)
![]() ;
;
![]() 8)
8)
![]() ;
;
![]()
9)
![]() ;
;
![]() 10)
10)
![]() ;
;
![]()
Пакет № 37.
Решить уравнение.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]()
Пакет № 38.
Решить уравнение
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]() 7)
7)
![]()
8)
![]() 9)
9)
![]() 10)
10)
![]()
Пакет № 39.
Найти частное решение уравнения, удовлетворяющее заданным начальным условиям.
1)
![]() ;
;
![]() ;
;
![]()
2)
![]() ;
;
![]() ;
;
![]()
3)
![]() ;
;
![]() ;
;
![]()
4)
![]() ;
;
![]() ;
;
![]()
5)
![]() ;
;
![]() ;
;
![]()
6)
![]() ;
;
![]() ;
;
![]()
7)
![]() ;
;
![]() ;
;
![]()
8)
![]() ;
;
![]() ;
;
![]()
9)
![]() ;
;
![]() ;
;
![]()
10)
![]() ;
;
![]() ;
;
![]()
Пакет № 40.
Найти общее решение уравнения.
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
