61

4.2. Примеры решения типовых задач

Часть I

Пример 1. Найдите область определения функции .

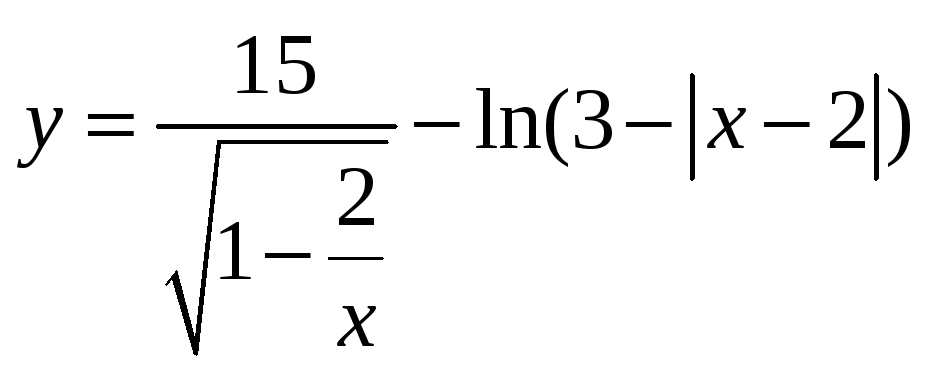Решение.

Ответ: .

Пример 2. Построить графики зависимости спроса Q_D(P) и предложения Q_S(P) от цены на товар Р , и найти при какой цене спрос равен предложению, если Q_D(P)=; Q_S(P)=.

Решение.

Построим в плоскости РОQ графики функций спроса и предложения (см. рисунок). В точке равновесия А (точке пересечения графиков) спрос равен предложению. Для нахождения координат этой точки решим систему:

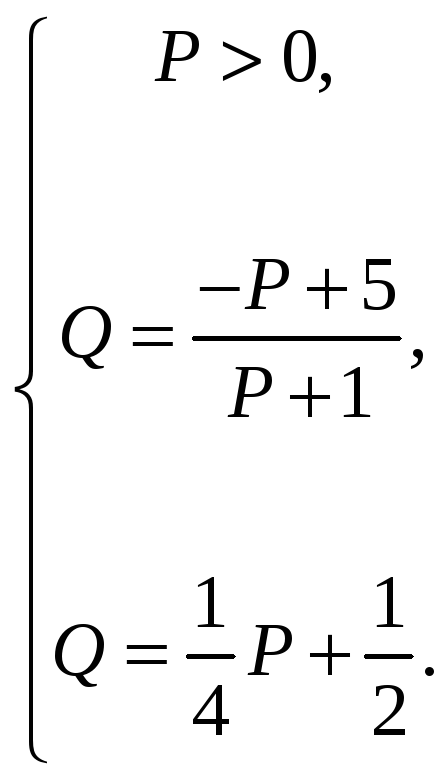
Из этой системы получаем: 

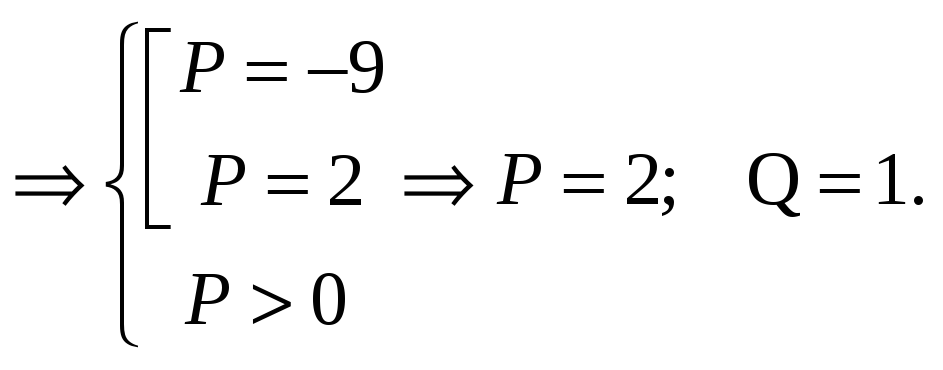
Ответ: P=2; Q=1.

Пример 3. Вычислить предел .

Решение.

==.

Ответ:.

Пример 4. Вычислить предел .

Решение.

==

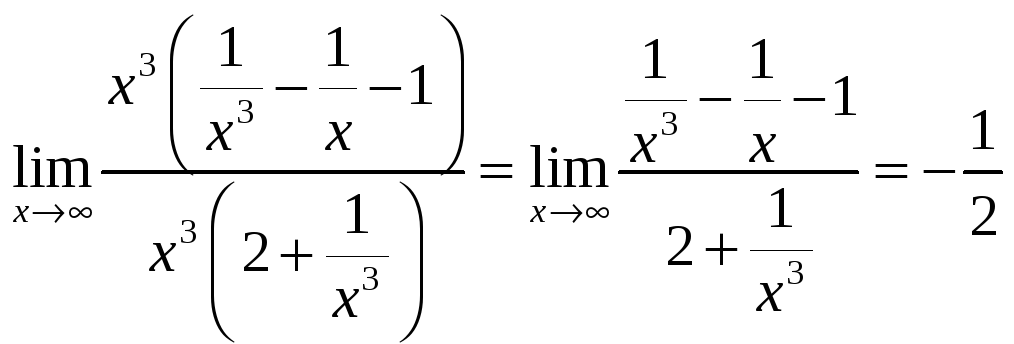
Ответ:.

Пример 5. Найти и построить асимптоты графика функции .

Решение. Так как точка разрыва , а ; ,

то - вертикальная асимптота.

Наклонные асимптоты можно задать уравнением , где , .

Если оба предела существуют, то наклонная асимптота (при этом, если - имеем горизонтальную асимптоту).

;

.

Следовательно, - наклонная асимптота.

Ответ: ,

Пример 6. Используя правила вычисления производной и таблицу, найдите производные следующих функций:

а) ; б); в)

Решение.

а);

б) 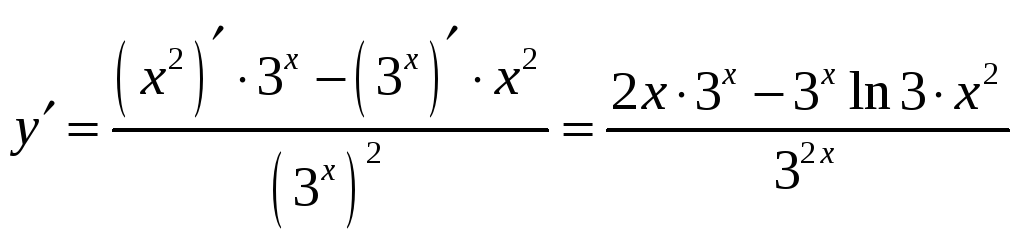; в).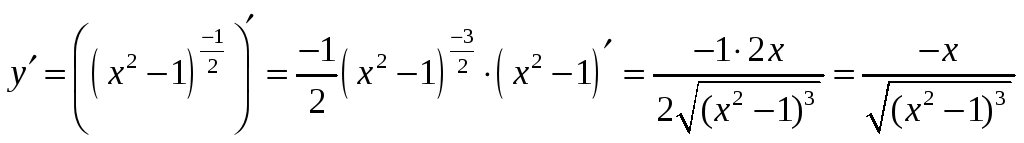

Ответ:

а); б) ; в).

Пример 7. Используя правило Лопиталя, найдите предел

Решение. .

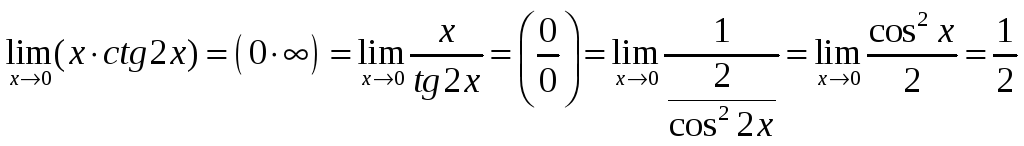Ответ:.

Пример 8. Составьте уравнение касательной к графику функции в точке ,

постройте графики кривой и касательной к ней:

Решение. Уравнение касательной в точке имеет вид .

; ; . Подставляя полученные данные в уравнение касательной, получим: .

Ответ:

Пример 9. Используя дифференциал функции, найдите приближенное значение величины .

Решение. Приближенное значение искомой величины ищем по формуле линеаризации .

Будем рассматривать как значение величины функции , при. Полагаем , представим как , где . Тогда , , , Подставляя полученные данные в формулу линеаризации, получаем .

Ответ:

Пример10.1 Найдите экстремум функции .

Решение. Найдем стационарные (критические) точки функции: ; ; , .

Найдем значение второй производной в критических точках: , , т.к. , то - будет точкой минимума; т.к. , то - будет точкой максимума.

Функция имеет максимум в точке, равный 2, и минимум в точке, равный 2.

Ответ:, .

Пример10.2. Найдите наибольшее и наименьшее значение функции на отрезке .

Решение. Найдем критические точки функции на данном отрезке и вычислим значения функции в этих точках и в граничных точках отрезка:

; , ,

, , .

Выберем из найденных значений наибольшее и наименьшее.

Ответ: , .

Пример11.

Провести полное исследование и построить график функции

Решение.

1. Функция определена и непрерывна для всех действительных значений х, кроме х=6.

2. График функции несимметричен, так как функция не является ни четной, ни нечетной. Функция также не является периодической.

3. График функции пересекает ось Ох в точках (5; 0); (7; 0).Чтобы найти эти точки, нужно решить уравнение .

График функции пересекает ось Оу в точке . Чтобы найти эту точку, нужно подставить в уравнение заданной функции значение .

4. Найдем интервалы знакопостоянства функции, решив неравенства

а) ; б) .

Итак, если ; , если ;

5. Рассмотрим поведение функции на границах области определения.

Как ведет себя функция вблизи точки разрыва х = 6 ?

Чтобы ответить на этот вопрос, найдем и. Следовательно, прямая является вертикальной асимптотой графика функции.

Как ведет себя функция при и при ?

Если рациональная функция представима в виде , где - бесконечно малая функция при (то есть ), то функция является наклонной асимптотой для графика функции . Функция представлена в виде суммы линейной и бесконечно малой функций , следовательно, прямая является для графика заданной функции наклонной асимптотой.

График функции приближается к прямой .

6. Интервалы монотонности и экстремумы найдем, используя теорию первой производной:

для любых значений аргумента из области определения. Вывод: функция монотонно убывает на всей области определения, экстремумов не имеет.

7. Исследование функции на выпуклость и точки перегиба проведем с помощью второй производной;

Определим знак второй производной.

если , то на интервале график функции направлен выпуклостью вверх;

если , то на интервале график функции направлен выпуклостью вниз. Точек перегиба кривая не имеет. Используя проведенное исследование, строим график функции .

Приведем еще один пример исследования функции и построения графика.

Провести полное исследование и построить график функции .

Решение

1. Функция определена и непрерывна для всех действительных значений х, кроме х=6.

2. График функции несимметричен, так как функция не является ни четной, ни нечетной. Функция также не является периодической.

3. График функции не пересекает ось Ох, так как уравнение действительных корней не имеет. График функции пересекает ось Оу в точке .

4. Найдем интервалы знакопостоянства функции, решив неравенства

а) ;

б).

Итак, ; .

5. Рассмотрим поведение функции на границах области определения.

Как ведет себя функция вблизи точки разрыва ?

Чтобы ответить на этот вопрос, найдем и. Следовательно, прямая является вертикальной асимптотой графика функции.

Как ведет себя функция при ?

График функции приближается к прямой , которая является для графика наклонной асимптотой. (Если рациональная функция представима в виде , где - бесконечно малая функция при , то функция является наклонной асимптотой для графика функции . Функция представлена в виде суммы линейной и бесконечно

малой функций, следовательно, прямая является для графика заданной функции наклонной асимптотой).

6. Интервалы монотонности и экстремумы данной функции найдем, используя теорию первой производной. Производная первого порядка имеет вид: .

, следовательно, на этих интервалах функция монотонно убывает;

, следовательно, на этих интервалах функция монотонно возрастает.

На интервале производная ;

на интервале производная ;

причем , следовательно, точка является точкой локального минимума исследуемой функции.

На интервале производная ;

на интервале производная ;

причем , следовательно, точка является точкой локального максимума исследуемой функции.

7. Исследование функции на выпуклость и точки перегиба проведем с помощью

второй производной;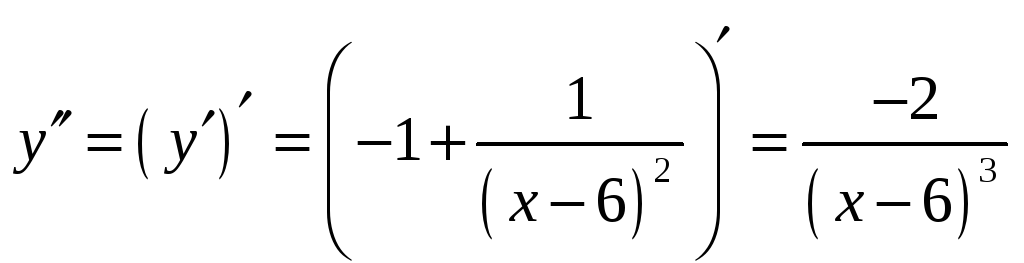

если , следовательно, на интервале график функции направлен выпуклостью вверх;

если , следовательно, на интервале график функции направлен выпуклостью вниз. Точек перегиба кривая не имеет. Используя проведенное исследование, строим график заданной функции.

Ъ