Теорема 2.1

Пусть a, b и с  неотрицательные постоянные.

Решение рекуррентных уравнений

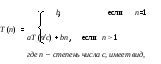
ПРИМЕЧАНИЕ :

(здесь и далее

после ^ - показатель степени. )

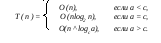
 Если n - степень числа c, то

1. Если a < c, то  rⁱ ( i= 0, ) - сходится к некоторой константе, и, следовательно, T(n) = O(n).

2. Если a = c, то каждым членом этой суммы будет 1, а всего в ней log_c n слагаемых.

Поэтому T(n) = O(n log ₂ n).

3. Если a > c, то

что составляет



Пример 3. Сортировка целых чисел.

1. Метод “пузырька”

Исследуется вся последовательность и находится наименьший элемент. Затем наименьший элемент меняется с первым, и процесс повторяется на остальных n-1 элементах.

Т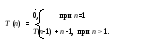огда

Решением этого уравнения служит T(n) = n(n-1)/2, что составляет O(n²).

Этот алгоритм можно считать рекурсивным применением приема “разделяй и властвуй” с разбиением задачи на неравные части.

2. Сортировка слиянием.

Пусть n = 2^k.

Исходная последовательность целых чисел x₁ , x₂ , ... , x_n разбивается на две подпоследовательности x₁ , x₂ , ... , x_n/2 и x_n/2+1 , ... , x_n. Теперь каждую из них надо упорядочить и затем слить их. Под “слиянием ” понимается объединение двух уже упорядоченных последовательностей в одну упорядоченную последовательность.

procedure Sort (i,j)

begin

if ( i==j ) then return x_i

else

begin

m  ( i + j - 1) / 2;

return Merge ( Sort( i, m), Sort (m+1,j))

end;

end;

Входом для процедуры Merge(S,T) служат две упорядоченные последовательности S и T, а выходом - последовательность элементов из S и T, расположенных в порядке неубывания. Так как S и T сами упорядочены, слияние требует сравнений не больше, чем || S || + || T || - 1. Работа этой процедуры состоит в выборе большего из наибольших элементов, остающихся в S и T , и последующем удалении выбранного элемента. В случае совпадения предпочтение можно отдавать предпочтение последовательности S.

Т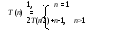аким образом,

Следовательно, T(n) = O (nlog ₂ n).

§ 3. Динамическое программирование

Рекурсивная техника полезна, если задачу можно разбить на подзадачи за разумное время, а суммарный размер подзадач будет небольшим. Из Теоремы 2.1 вытекает, что если сумма размеров подзадач равна an для некоторой постоянной a>1, то рекурсивный алгоритм, вероятно, имеет полиномиальную временную сложность. Но если очевидное разбиение задачи размера n сводит ее к n задачам размера n-1, то рекурсивный алгоритм, вероятно, имеет экспоненциальную сложность. В этом случае можно получить более эффективные алгоритмы с помощью табличной техники, называемой динамическим программированием.

Динамическое программирование вычисляет решение для всех подзадач. Вычисление идет от малых подзадач к бо'льшим, и ответы запоминаются в таблице. Преимущество этого метода состоит в том, что раз уж подзадача решена, ее ответ где-то хранится и никогда не вычисляется заново.

Пример 1. Произведение матриц.

Предположим, что умножение (pq)-матрицы на (qr)-матрицу требует pqr операций.

Рассмотрим произведение

M = M₁  M₂  M₃  M₄,

[10  20] [20  50] [50  1] [1  100]

где размеры каждой матрицы Mi указаны в скобках.

Если вычислять M в порядке :

M₁  (M₂  ( M₃  M₄ )) , то потребуется 125000 операций,

тогда как вычисление в M в порядке :

( M₁  ( M₂  M₃ ))  M₄ занимает лишь 2200 операций.

1. Процесс перебора всех порядков, в которых можно вычислить рассматриваемое произведение n матриц, с целью минимизировать число операций имеет экспоненциальную сложность.

К оличество вариантов расстановки скобок есть число Карталена :

X(1) = 1;

 X(n)  2^n-2

2. Динамическое программирование приводит к алгоритму сложности O(n³).

Пусть m_ij - минимальная сложность вычисления M_i  M_i+1  ...  M_j , 1  i  j  n.

Здесь m _ik - минимальная сложность вычисления M’ = M _i  M_i+1  ...  M_k,

m _k+1,j - минимальная сложность вычисления M’’ = M_k+1  M_k+2  ...  M_j ,

r _i-1 r_k r_j - сложность умножения M’ на M’’.

В динамическом программировании m_ij вычисляются в порядке возрастания разностей нижних индексов. Начинают с вычисления m_ii для всех i, затем m_i,i+1 для всех i, потом m_i,i+2 и т.д. При этом m_ik и m_k+1,j в (*) будут уже вычислены, когда мы приступим к вычислению m_ij . Это следует из того, что при i k<j разность j-i должна быть больше k-i, а также и j-(k+1).