§ 8. Диафантовы множества.

Рассмотрим уравнение

D(x₁, x₂,…. x_n) = 0, где D  полином с целочисленными коэффициентами.

Нас будет интересовать проблема разрешимости в целых числах.

Попытаемся обобщить задачу. Рассмотрим систему диафантовых уравнений:

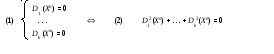
Задача (2) не сложнее задачи (1), множества их решений совпадают. Значит, эти задачи эквивалентны.

Теперь займемся понижением степени уравнения. Диафантовы уравнения первой степени разрешимы. Оказывается, любое диафантово уравнение может быть сведено к диафантову уравнению 4-ой степени.

Степень полинома D  максимум из сумм степеней сомножителей по всем слагаемым D.

Теорема Лагранжа.

Для любого a существует его представление в виде суммы четырех квадратов.

a = x₁² + x₂² + x₃² + x₄².

8.1. Разрешимость в натуральных числах.

По любому диафантову уравнению можно построить диафантово уравнение в целых числах.

Сведение задачи в целых числах к задаче в натуральных  это всегда сведение вида :

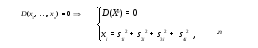
и наоборот.

Верно ли, что уравнение D(Xⁿ) = 0 разрешимо в целых числах?

Уравнение D( a₁  b₁, a₂ – b₂, ... , a_n – b_n ) = 0  разрешимо в целых числах.

Если одну задачу можно свести к другой , то они эквивалентны.

Задачи распознавания – это задачи, в которых надо решить, существует ответ или нет.

Для решения задачи вводится некий язык L  ^*

П  L  ^* .

Определение.

Будем говорить, что язык L₁  ^*₁ сводится( ) к языку L₂  ^*₂ тогда и только тогда, когда существует вычислимая функция

f : ₁^*  ₂^* такая, что

для любого x  ₁^* выполняется: x  L₁ тогда и только тогда, когда f(x)  L₂.

Аналогично можно говорить о сводимости задачи, следовательно, можно говорить и о сводимости языков, которые они определяют. Если функция f существует, но не вычислима, то данное определение не имеет смысла.

Мы считали, что задачи эквивалентны в вычислительном смысле, если П₁  П₂ и П₂  П₁, т.е. разрешимы и неразрешимы одновременно.

У диафантовых уравнений у нас присутствует не только одновременное существование решений, но и построение одного решения по другому. Поэтому будем считать, что все переменные в диафантовом уравнении . Любое диафантово уравнение можно представить в виде :

D(a₁, …, a_n, x₁, …, x_m) =0, где {a_i }_{i = 1...n} – параметры, {x_j }_{j = 1…m}  переменные.

Тогда существует множество кортежей из натуральных чисел < a₁, … , a_n >  ⁿ , при которых (как параметрах) диафантово уравнение разрешимо.

Определение.

Множество ⁿ ⁿ называется диафантовым, если существует полином с целыми коэффициентами D(Aⁿ,X^m) такой, что <a₁, …, a_n > ⁿ   X^m такой, что D(Aⁿ,X^m) = 0, т.е. параметрическое диафантово уравнение разрешимо.

Множество ⁿ  это множество кортежей. Если n = 1, то это множество чисел.

Теорема 8.1.

Пусть M₁ⁿ и M₂ⁿ  диафантовы множества. Тогда M₁ⁿ M₂ⁿ и M₁ⁿ  M₂ⁿ тоже являются диафантовыми.



1) M₁ⁿ M₂ⁿ

Так как множества M₁ и M₂ диафантовы, то существует их диафантовы уравнения, и либо одно, либо другое разрешимо. Тогда представим M₁ и M₂ полиномами D₁(A, X^m1) и D₂(A, X^m2). Объединение будет описываться следующим образом:  X^m такой , что D₁(A, X^m1)* D₂(A, X^m2) = 0 , где M = Max{ M₁, M₂ }. Если хоть одно из уравнений D_i(A, X^mi) = 0, i = 1,2  разрешимо, то и это уравнение будет разрешимо.

2) M₁ⁿ  M₂ⁿ

Здесь общее уравнение и переменные другие: D₁(A, X^m1) + D₂(A, Y^m2) = 0

