Физика 3 семестр / новая папка / Помощь к экзамену / Темы / 10.Электрическая емкость

3.2. Электроемкость. Конденсаторы

Рассмотрим процесс зарядки произвольного проводника. Если сообщить проводнику заряд , то заряд распределится по поверхности проводника с поверхностной плотностью, где r –координата точки поверхности проводника в выбранной системе координат. В соответствии с выводами п.3.1 вид функции зависит только от геометрии проводника, т.е. его размеров и формы (кривизны поверхности). Такое распределение зарядов по поверхности проводника создаст в пространстве вокруг проводника электростатическое поле с напряженностью , где r – координата точки пространства в той же системе координат. Функцию можно найти, используя теорему Остроградского–Гаусса, при этом вид функции будет зависеть только от формы и размеров проводника. Определим потенциал проводника с помощью интегральной связи напряженности и потенциала:

, (3.3)

где – координата какой-либо точки проводника (они все имеют одинаковые потенциалы).

Если сообщить проводнику заряд , то заряд распределится по поверхности проводника с поверхностной плотностью, создав вокруг себя поле с напряженностью . Потенциал проводника в этом случае будет равен

. (3.4)

Важно, что вид функций поверхностной плотности зарядов и напряженности поля зависит только от формы и размеров проводника. Это означает, что функции , , …, будут одинаковы по внешнему виду. Различие между ними будет лишь в коэффициентах, определяемых зарядами , , …,. Аналогичный вывод можно сделать и для функций напряженности поля. Следовательно, результаты интегрирования однотипных функций в выражениях (3.3), (3.4) и им подобных будут пропорциональны соответствующим зарядам , , …,. Вид пропорциональности определяется только формой и размерами проводника. Поэтому для данного проводника

.

Электроемкостью уединенного проводника называется физическая величина, равная отношению заряда проводника к его потенциалу в поле этого заряда:

. (3.5)

Электроемкость проводника показывает, какой заряд необходимо сообщить проводнику для того, чтобы его потенциал принял заданное значение. Чем больше заряд проводника, тем больше его потенциал в поле этого заряда. Поэтому электроемкость не зависит ни от величины заряда проводника, ни от значения его потенциала, а зависит только от размера и формы проводника, а также от диэлектрических свойств среды, в которой он находится. Единица измерения электроемкости проводника в СИ называется фарад (обозначается 1 Ф): .

Рассмотрим определение емкости проводящего шара радиусом R, находящегося в вакууме. Для этого сообщим шару произвольный заряд Q. Заряд равномерно распределится по поверхности шара с поверхностной плотностью , которая будет одинакова в каждой точке поверхности шара. Этот заряд создаст электростатическое поле, напряженность которого определяется следующим образом (см. пример 1, п. 1.7):

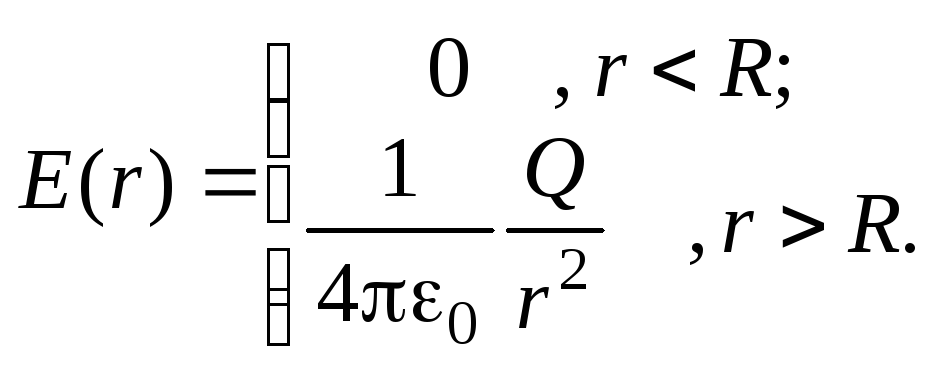
Вид функции – гипербола (), а коэффициент пропорциональ-ности зависит только от заряда шара. Потенциал шара можно будет найти так:

.

В соответствии с (3.5) емкость шара

. (3.6)

При определении емкости проводника описанным выше способом важно, чтобы вблизи него не находились другие проводники, т.е. чтобы проводник был уединенным. Рассмотрим, как изменится емкость проводника, если он будет находиться рядом с незаряженным проводником. Допустим, что проводник 1 обладает положительным зарядом (рис. 3.8). Тогда в незаряженном проводнике 2 произойдет разделение зарядов (электростатическая индукция) на отрицательные и положительные , причем . В этом случае потенциал проводника 1 определится по принципу суперпозиции как сумма его потенциалов в трех полях: в поле собственного заряда Q, в поле заряда и в поле заряда :

.

Заметим, что , а . Однако, поскольку отрицательные индуцированные заряды располагаются ближе к проводнику 1, чем положительные индуцированные заряды , то . Поэтому . В результате потенциал заряженного проводника уменьшается, а емкость проводника увеличивается.

Аналогичный вывод можно получить и в случае, если вблизи положительно заряженного проводника располагается незаряженное диэлектрическое тело. На поверхности диэлектрика образуются связанные поляризационные заряды, суммарный потенциал проводника в поле которых также отрицателен.

Следует отметить, что если зарядить проводник отрицательным зарядом, то вывод будет противоположным: потенциал проводника возрастет.

Таким образом, электроемкость проводника зависит от наличия в пространстве вблизи него любого тела (проводника или диэлеткрика).

В случае, если заряженные проводники располагаются таким образом, что электрическое поле существует только в пространстве между ними, то они образуют конденсатор. Сами проводники при этом называются обкладками конденсатора. Примеры расположения двух обкладок, образующих конденсаторы, приведены на рис. 3.9 а, б, в. Это, соответственно, плоский, цилиндрический и сферический конденсаторы. Плоский конденсатор создается системой двух бесконечно больших параллельных пластин площадью S, находящимися на малом расстоянии d друг от друга (). Цилиндрический конденсатор образован двумя бесконечно длинными коаксиальными цилиндрами (), а сферический – двумя концентрическими сферами. Если обкладки каждой из этих систем зарядить разноименными одинаковыми по модулю зарядами, то электрическое поле образуется только в пространстве между ними. Модуль заряда любой из обкладок называется зарядом конденсатора.

Электроемкостью конденсатора называется физическая величина, равная отношению заряда конденсатора к разности потенциалов, создаваемой полем этого заряда между его обкладками:

. (3.7)

Так же, как и емкость проводника, электроемкость конденсатора не зависит ни от величины заряда конденсатора, ни от разности потенциалов между его обкладками, а зависит только от размера и формы конденсатора, а также от диэлектрических свойств среды между обкладками конденсатора. Следует отметить, что электроемкость конденсатора не зависит от наличия вблизи него других проводящих или диэлектрических тел.

В качестве примера выведем формулу емкости плоского конденсатора, изображенного на рис. 3.9, а. Определим напряженность электростатического поля, создаваемого одной заряженной пластиной площадью S. Силовые линии такого поля изображены на рис. 3.10. Если рассмотреть точки пространства, расположенные настолько близко к пластине, что расстояние от них до пластины существенно меньше, чем до ее границ (из этих точек пластина будет представляться как бесконечно большая плоскость), то искривлением силовых линий у границ пластины можно пренебречь (рис. 3.11). Таким образом, бесконечно большая заряженная плоскость создает однородное поле. Исходя из симметричности системы, модуль напряженности поля во всех точках, равноудаленных от пластины, должен быть одинаковым, а направление вектора зависит только от положения исследуемой точки пространства (слева или справа от пластины).

Определим напряженность поля в некоторой точке с координатой x, отсчитываемой вдоль оси , направленной перпендикулярно пластине. Для этого в качестве гауссовой поверхности выберем поверхность цилиндра, ось которого перпендикулярна плоскости, а основание имеет площадь (рис. 3.12). Модуль напряженности поля одинаков во всех точках оснований цилиндра, исходя из симметрии системы. Угол между и внешней нормалью к поверхности во всех точках боковой поверхности цилиндра равен , а во всех точках левого и правого оснований гауссова цилиндра равен 0.

Определим поток напряженности поля через выбранную поверхность.

,

где – площадь левого основания гауссова цилиндра; – площадь правого основания гауссова цилиндра; – площадь боковой поверхности гауссова цилиндра. Получаем

; ;.

Таким образом,

. (3.8)

Определим алгебраическую сумму зарядов, охваченных поверхностью гауссова цилиндра. В данном случае электрический заряд, попавший внутрь него – это заряд “вырезанной” цилиндром части пластины. Его можно найти, умножив площадь основания цилиндра на поверхностную плотность заряда пластины:

. (3.9)

Приравняем (3.8) и (3.9) с учетом коэффициента :

. (3.10)

Полученное соотношение определяет модуль напряженности однородного поля бесконечно большой заряженной пластины.

Если две разноименно заряженные пластины расположить на малом расстоянии друг от друга так, чтобы выполнялось условие однородности поля каждой из них (рис. 3.13), то напряженность поля можно будет определить по принципу суперпозиции с учетом (3.10):

В этом случае разность потенциалов между обкладками получившегося конденсатора можно определить так:

.

Емкость плоского конденсатора, по определению (3.7), составит

.

Следует учесть, что если пространство между обкладками любого конденсатора заполнить диэлектриком с относительной диэлектрической проницаемостью , то при том же значении заряда обкладок напряженность поля между обкладками уменьшится в  раз. Поэтому в  раз уменьшится разность потенциалов между ними, а, следовательно, в  раз увеличится емкость конденсатора:

.

Тогда

. (3.11)

Выведем формулу емкости сферического конденсатора. Рассмотрим систему сферических обкладок, изображенную на рис. 3.9, в. Поместим на внутреннюю обкладку заряд Q, а на внешнюю заряд . Напряженность электростатического поля, созданного такой системой зарядов можно описать следующей формулой:

Определим разность потенциалов между обкладками, пользуясь дифференциальной связью напряженности и потенциала (1.13):

.

Емкость сферического конденсатора, по определению (3.7), составит

.

Если конденсатор заполнен диэлектриком с относительной диэлектрической проницаемостью , то

. (3.12)

Подчеркнем еще раз, что емкость конденсатора зависит от размера, формы конденсатора и относительной диэлектрической проницаемости диэлектрика между его обкладками.