
-
Метод осьової симетрії
Метод осьової симетрії розв'язування задач полягає в тому, що поряд з даними точками (фігурами) в розгляд вводять симетричні їм точки (фігури) відносно деякої прямої.
При застосуванні цього методу один з даних елементів або кілька з них замінюють елементом, симетричним даному відповідно деякої осі. За вісь симетрії приймають або дану пряму, або таку, яку легко побудувати.
Побудовану фігуру пристосовують до тих же умов, які накладені на дану фігуру, і, таким чином, розв’язування даної задачі зводиться до розв’язування нової задачі.
Проілюструємо можливості розв’язування задач методом осьової симетрії.
Задача 1. Усередині гострого кута взято точку М. Побудувати трикутник KLM, що має найменший периметр, а вершини K і L якого лежать на сторонах даного трикутника.
Аналіз.
На точку М подіємо симетрією відносно
прямих (ОВ) і (ОА). М'= ,
M"=
,
M"= .
Тоді
.
Тоді
 =
= ,
де
,
де
 .
.
 =
= ,
де L
,
де L
 .
.
Отже,
 і дорівнює периметру ламаної
і дорівнює периметру ламаної
 ,
кінці
,
кінці
 та
та якої визначаються однозначно точкою М
і сторонами кута АОВ. Ця величина є
найменшою, якщо точки
якої визначаються однозначно точкою М
і сторонами кута АОВ. Ця величина є
найменшою, якщо точки
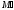 ,К,
L,
,К,
L,
 належать одній прямій.
належать одній прямій.
План
побудови. 
1.
 =
=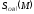 ,
,
 =
=
 .
.
2.
К=

3.
L=
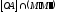
4. ∆KLM.
Всі інші етапи розв’язування цієї задачі опустимо.
Задача
2. Дана
пряма MN і дві точки A i
B
по один бік від неї. Знайти на прямій MN
таку точку X,
щоб відрізки AX
і BX
утворювали з цією прямою кути, один з
яких вдвоє більше другого:
 .
.
Аналіз.
Нехай точка Х- шукана, тобто
 .
Подіємо симетрією відносно
.
Подіємо симетрією відносно
 на одну з даних точок (наприклад, точку
на одну з даних точок (наприклад, точку
 ):
):
 .
Тоді
.
Тоді .
Нехай
.
Нехай
 ,
,
 між
між
 .
Тоді
.
Тоді
 бісектриса
бісектриса
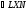 .
Отже, точка
.
Отже, точка
 -
центр кола, вписанного в
-
центр кола, вписанного в
 ,
яке можна побудувати. Провівши із точки
,
яке можна побудувати. Провівши із точки
 дотичну
до цього кола, точку
дотичну
до цього кола, точку
 одержимо як точку перетину її з даною
прямою.
одержимо як точку перетину її з даною
прямою.
План
побудови
1.
 .
.
2.
 .
.
3.
 дотична до
дотична до .
.
4.
 .
.
Доведення.
Очевидно, що
 ,
бо
,
бо
 і
і
 є вертикальними. Промінь
є вертикальними. Промінь
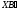 є бісектрисою
є бісектрисою
 ,
бо
,
бо
 є центром кола, яке дотикається сторін
цього кута. Отже
є центром кола, яке дотикається сторін
цього кута. Отже
 .
Оскільки
.
Оскільки
 ,
то
,
то
 ,
тому
,
тому
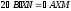 .
.
Задача
3. Дано
гострий кут і
точки A
i
B
всередині цього кута. Знайти на стороні
і
точки A
i
B
всередині цього кута. Знайти на стороні
 таку точку
таку точку ,
щоб
,
щоб
 ,
де
,
де
 і
і
 -
точки перетину
-
точки перетину
 і
і
 з
з
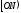 ,
був рівнобедрений:
,
був рівнобедрений:
 .
.
Аналіз.
Позначимо
 .
Для точки
.
Для точки треба знайти другу умову, бо одна умова
є:
треба знайти другу умову, бо одна умова
є:
 .
Поділяємо на одну з даних даних точок,
наприклад, на точку
.
Поділяємо на одну з даних даних точок,
наприклад, на точку
 симетрією відносно
симетрією відносно
 :
:
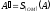 .
Виразимо
.
Виразимо
 через
через
 .
.

 рівнобедрений
рівнобедрений
 .
.
План побудови.
1.

2.
 .
.
3.
 ;
;
 .
.
4.
 .
.
Доведення.
Потрібно довести, що -
рівнобедрений. З п. 1
-
рівнобедрений. З п. 1 .
Тоді
.
Тоді
 Отже,
Отже,
 .
.
Дослідження. Задача має один розвязок.
Задача
4. Побудувати
прямокутний трикутник за катетом
 і різницею
і різницею
 двох сторін.
двох сторін.
Аналіз.
Нехай
 -
шуканий, тобто
-
шуканий, тобто
 ,
,
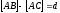 .
Щоб побудувати на малюнку різницю
гіпотенузи і катета, побудуємо
.
Щоб побудувати на малюнку різницю
гіпотенузи і катета, побудуємо
 симетричний
симетричний
 відносно бісектриси кута
відносно бісектриси кута
 .
Т.
.
Т. .
Тому
.
Тому
 .
Побудова
.
Побудова
 визначить дві вершини шуканого
визначить дві вершини шуканого .
Оскільки
.
Оскільки
 ,
то точка
,
то точка
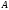 належить середньому перпендикуляру
до
належить середньому перпендикуляру
до .
.
План побудови.
1.
 .
.
2.
 -
середина
-
середина
 ;
;
 .
.
3.

4.
 .
.
Інші етапи розв’язування опускаємо.
Задачі для самостійного розв'язування
-
Дано три прямі
 ,
які попарно перетинаються. Як побудувати
відрізок, перпендикулярний до прямої
,
які попарно перетинаються. Як побудувати
відрізок, перпендикулярний до прямої
 ,
середина якого лежить на прямій
,
середина якого лежить на прямій
 ,
а кінці на прямих
,
а кінці на прямих
 і
і
 ?
? -
Побудувати чотирикутник АВСВ за чотирма сторонами так, щоб промінь АС був бісектрисою кута А.
-
Побудувати АВС, знаючи [ВС] = а, [АС] = b і В - А = (
 >
>
 ).
). -
Населені пункти А і В розташовані по один бік від залізниці. В якому пункті цієї траси слід побудувати залізничну станцію С так, щоб сума відстаней [АС] і [ВС] була найменшою?
-
На прямій АВ знайти точку X так, щоб дотичні, проведені з неї до двох даних кіл, утворили з прямою АВ рівні кути.
-
Побудувати ромб з даною діагоналлю, яка лежала б на даній прямій так, щоб інші дві вершини ромба були розміщені на двох даних колах.
-
Через дані точки А і В провести дві прямі так, щоб кут між ними ділився даною прямою навпіл.
-
Побудувати чотирикутник АВСD, знаючи [АВ] = а, [АD] =b, B=D, якщо відомо, що в нього можна вписати коло.
-
Побудувати квадрат, дві протилежні вершини якого лежали б на даній прямій, а дві інші - на даних колах.
-
Побудувати квадрат так, щоб дві протилежні вершини його лежали на даній прямій a, а дві інші - на сторонах даного АВС.
