2.4.4. Эллиптическое поле
Круговое вращающееся
магнитное поле возникает только при
симметрии токов, проходящих по катушкам
(симметрии НС катушек отдельных
фаз), при симметричном расположении
этих катушек в пространстве и при сдвиге
во времени между фазовыми токами, равном
пространственному сдвигу между катушками.
При несоблюдении хотя бы одного из этих
условий возникает не круговое, а
эллиптическое вращающееся поле
(рис.2.22а), у которого максимальное
значение результирующей индукции для
различных моментов времени не остается
постоянным, как при круговом поле. В
таком поле пространственный вектор НС
или индукции
описывает эллипс. Эллиптическое поле
можно представить в виде
а) б) в)
Рис. 2.22. Эллиптическое магнитное поле в рабочем зазоре машины (а) и его разложение на два составляющих круговых поля: прямое (б) и обратное (в).
двух эквивалентных круговых полей, вращающихся в противоположных направлениях рис.2.22б, в). Разложение эллиптического поля на прямое и обратное круговые поля производится методом симметричных составляющих, с помощью которого определяются НС прямой и обратной последовательностей. Рассмотрим, как осуществляется это разложение на примере двухфазной обмотки при питании ее несимметричными токами.
Допустим, что НС
фазы B-Y
опережает НС
фазы A-X
на какой-то угол
,
т. е.
(2.33)
причем
в общем случае
.
Представим каждый
из векторов НС
и
в виде суммы двух векторов прямой и
обратной последовательностей:
(2.34)
При этом
(2.35)
Векторы
и
образуют систему НС прямой
последовательности (рис. 2.23a),
причем
опережает вектор
на угол
.
Векторы
и
а) б)
Рис. 2.23. Диаграмма разложения векторов НС двухфазной обмотки на систему векторов прямой (а) и обратной (б) последовательностей.
образуют
систему векторов НС обратной
последовательности (рис. 2.23б), причем
вектор
опережает вектор
на угол
.
Величины векторов
прямой и обратной последовательностей
найдем, подставив последнюю систему в
выражения для
и
(2.34):
(2.36)
Умножим первое
уравнение системы на
:
(2.37)
Получаем
;
.
Так как
,
(2.38)
то уравнения бегущей волны для прямого и обратного круговых полей имеют вид:
(2.39)
При рассмотрении работы многофазных электрических машин, обычно заданными величинами являются напряжения, подводимые к машине, и сопротивления фаз. В общем случае для определения свойств машины требуется разложить на симметричные составляющие подводимые напряжения, по которым затем определяются токи и НС прямой и обратной последовательностей.
Перейдем от системы НС (2.34) к системе токов:
(2.40)
где
и
- эффективные числа витков обеих фаз с
учетом обмоточных коэффициентов.
Так как
(2.41)
то
(2.42)
где
.
В каждой из фаз токи прямой и обратной последовательностей создают падения напряжений, сумма которых равна подведенному напряжению:
(2.43)
где
- сопротивления
фаз A и B
для токов прямой и обратной
последовательностей.
С учетом выражений
и
(2.42):
(2.44)
Из соотношений
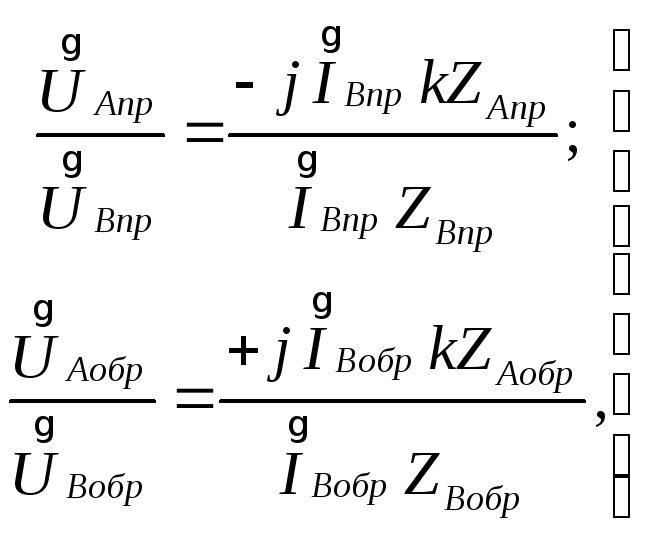(2.45)
имеем
(2.46)
Подставим полученные
зависимости для
и
в выражение для
и
(2.43):
(2.47)
В полученных выражениях при одинаковом количестве, площади и конфигурации пазов, занимаемых каждой фазовой обмоткой, отношение сопротивлений
,
(2.48)
т. к. активное r и индуктивное x сопротивления каждой фазы пропорциональны квадрату числа витков:
;
(2.49)
,
(2.50)
где
- удельное
сопротивление проводника фазовой
обмотки;
- средняя длина
витка;
S – поперечное сечение проводника;
П – суммарная площадь (активная) всех пазов данной фазы;
- магнитная
проводимость для потока рассеяния,
создаваемого фазовой обмоткой;
- постоянные.
С учетом соотношения
для
(2.48), выражение для
(2.47) примет вид:
;
.
(2.51)
Складывая и вычитая полученное выражение и второе уравнение из (2.47), находим:
(2.52)
Теперь можно определить и симметричные составляющие токов:
(2.53)
Таким образом,
зная параметры машины и подводимые к
фазам напряжения
и
,
можно определить токи и намагничивающие
силы фаз при несимметричном питании.
Аналогично можно найти токи и НС фаз при несимметричном питании трехфазных электрических машин. При этом фазовые напряжения следует разложить на три составляющие (прямой, обратной и нулевой последовательностей), из которых вращающие магнитные поля создают только первые две составляющие.