
- •Означення матриці. Основні поняття.
- •Означення визначників 2-го і 3-го порядків. Їх обчислення.
- •Властивості визначників.
- •Розкладання визначника за елементами рядка або стовпця.
- •Правило Крамера для розв’язання систем лінійніх рівнянь.
- •Означення оберненої матриці та спосіб її знаходження.
- •Матричний метод.
- •Означення рангу матриці.
- •Обчислення рангу методом елементарних перетворень.
- •Дослідження системи лінійних рівнянь на сумісність.
- •Однорідні системи лінійних рівнянь
- •Лінійні дії з векторами.
- •Означення границі функції, основні властивості.
- •Нескінченно малі величини та їх порівняння.
- •Нескінченно великі величини та їх порівняння.
- •Перша особлива границя та її наслідки.
- •Друга особлива границя та її наслідки.
- •Означення похідної функції.
- •Механічний, геометричний та економічний зміст похідної.
- •Правила диференціювання. Основні правила диференціювання
- •Означення монотонної функції. Достатня ознака монотонності.
- •Означення точки екстремуму. Достатня ознака екстремуму.
- •Дослідження функції на опуклість, угнутість, точки перегину.
- •Асимптоти графіка функції.
- •Загальна схема дослідження функції та побудови графіка.
- •Метод інтегрування заміною змінних.
- •Приклади
- •Метод інтегрування частинами.
- •Означення визначеного інтеграла.
- •Властивості визначеного інтеграла.
- •Основні властивості визначеного інтеграла
- •Дорівнює зміні загальних витрат при зростанні кількості виробленої продукції від a до b одиниць.
- •Одержуємо
- •Таким чином, якщо f(t) - продуктивність праці в момент часу t, то - об’єм продукції, що виробляється за проміжок часу [0, т];
- •Невластиві інтеграли (означення, основні поняття, геометрична інтерпретація).
- •Основні означення та поняття розділу «Диференціальні рівняння»
- •Диференціальне рівняння 1-го порядку з відокремленими змінними (вигляд, метод розв’язання)
- •Лінійні рівняння 1-го порядку (вигляд, метод розв’язання)
- •Однорідні рівняння 1-го порядку (вигляд, метод розв’язання)
- •Основні поняття та початкові твердження розділу “Ряди” (означення числового ряду, збіжного та розбіжного ряду, суми ряду; властивості числових рядів).
- •Необхідна умова збіжності числового ряду.
-
Властивості визначеного інтеграла.
-
Основні властивості визначеного інтеграла
-
-
1)
 =
= =
= ,
тобто визначений інтеграл не залежить
від позначення змінної інтегрування.
,
тобто визначений інтеграл не залежить
від позначення змінної інтегрування. -
2)
 .
. -
3)
 =
-
=
- .
. -
4)
 =
= +
+ (якщо кожний із вказаних інтегралів
існує).
(якщо кожний із вказаних інтегралів
існує). -
5)
 =
=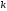
 ,
де
,
де
 ― число.
― число. -
6)
 =
= +
+ ,
де точка
,
де точка
 ― довільна точка осі ОХ (якщо кожен із
цих інтегралів існує).
― довільна точка осі ОХ (якщо кожен із
цих інтегралів існує). -
7) Теорема про оцінку визначеного інтеграла.
-
Нехай
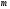 і
і ― найменше та найбільше значення
― найменше та найбільше значення
 на
на
 ,
тобто
,
тобто
 для всіх
для всіх
 .
Тоді
.
Тоді -
 .
. -
8) Теорема про середнє для визначеного інтеграла.
-
Нехай функція
 неперервна на відрізку
неперервна на відрізку
 .
Тоді на
.
Тоді на
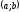 знайдеться точка
знайдеться точка
 така, що
така, що
-
 =
=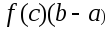 ,
,

-
(тобто
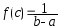
 ).
). -
-
Значення
 називається середнім значенням функції
називається середнім значенням функції
 на відрізку
на відрізку
 .
.
-
Теорема Ньютона-Лейбніца.
-
Нехай
 ― первісна для функції
― первісна для функції
 на відрізку
на відрізку
 ,
тобто
,
тобто
 =
=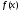 для
для

 .
Тоді
.
Тоді -
 =
= -
- =
= │
│ .
.
-
Метод заміни змінної у визначеному інтегралі.
-
Метод заміни змінної. Нехай виконуються умови :
-
а)функція
 є неперервною на
є неперервною на
 ;
б)функція
;
б)функція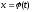 та її похідна
та її похідна
 є неперервними на відрізку
є неперервними на відрізку
 ,
причому
,
причому
 ;
в)
;
в) є монотонною на
є монотонною на
 .
Тоді
.
Тоді -
 =
= .
. -
-
Звертаємо увагу на те, що при переході до нової змінної у визначеному інтегралі змінюються межі інтегрування.
-
Приклади
-

-
б)

-
Зауваження. При заміні змінної у визначеному інтегралі немає потреби (на відміну від невизначеного інтеграла), повертатися до старої змінної.
-
Метод інтегрування частинами у визначеному інтегралі.
-
Метод інтегрування частинами. Формула інтегрування частинами для визначеного інтеграла має вигляд:
 Приклади
Приклади -
а)
 .
. -
-
Геометричні застосування визначених інтегралів.
-
Обчислення площин плоских фігур.
-
Всюди в цьому розділі всі функції та їх похідні вважаємо неперервними.
-

-
-
-
-
-
-
-
-
-
Рис.1
-
-
-
-

-
-
-
-
-
-
-
-
Рис.2
-
Обчислимо площу S криволінійної трапеції, обмеженої зверху графіком неперервної і невід¢ємної функції y=f(x), заданої на [а; b], знизу – відрізком
-
[а; b], з боків-вертикальними прямими х = а та х = b (рис.1). Розіб¢ємо відрізок [а; b] на n довільних частин за допомогою точок х0 , х1 ,…..,х n (а = х0 <x1<…..< <x n-1<x n= b). Через кожну точку поділу проведемо вертикалі, які розбивають фігуру на n малих криволінійних трапецій. Розглянемо довільний відрізок [х к-1; х к] (к =1,
 ),
вважаючи його довжину D
х к
= х к
– х к-1
достатньо
малою. Оберемо на ньому довільну точку
a
к
Î[х
к-1;
х к
].
Тоді площа к-ї криволінійної трапеції
наближено дорівнює f
(a
к)D
х к ,
тобто площі прямокутника з тією ж
основою [х
к-1;
х к
]
і висотою f
(a
к),
причому наближення поліпшується, якщо
зменшується D
х к . Тоді
),
вважаючи його довжину D
х к
= х к
– х к-1
достатньо
малою. Оберемо на ньому довільну точку
a
к
Î[х
к-1;
х к
].
Тоді площа к-ї криволінійної трапеції
наближено дорівнює f
(a
к)D
х к ,
тобто площі прямокутника з тією ж
основою [х
к-1;
х к
]
і висотою f
(a
к),
причому наближення поліпшується, якщо
зменшується D
х к . Тоді -
 .
. -
Звернувши увагу на те, що в правій частині останньої рівності одержано інтегральну суму для f (x) на відрізку [a ;b] і вважаючи природним за точне значення площі S прийняти її границю ( при max D x k®0), одержуємо (див. означення визначеного інтеграла в І.1):
-
 .
. -
У загальному випадку, коли фігура обмежена зверху кривою
 знизу
кривою
знизу
кривою
 з боків – прямими х=а, х= b
(див.рис.2), її площа обчислюється за
формулою
з боків – прямими х=а, х= b
(див.рис.2), її площа обчислюється за
формулою -

-
ІІ. Обчислення довжин дуг кривих.
-
Довжина дуги кривої у = f (x)
 обчислюється за формулою
обчислюється за формулою
-
 .
.
-
ІІ. Обчислення об’ємів тіл обертання.

-
-
-
-
-
-
-
Об¢єм тіла, одержаного обертанням навколо осі ОХ криволінійної трапеції, обмеженої кривою y = f (x) та прямими х=а, х=b (див.мал.3), обчислюється за формулою:
-
 .
.
-
ІІ. Обчислення площі поверхні обертання.
-
Площа бічної поверхні тіла, одержаного обертанням навколо осі ОХ криволінійної трапеції, що обмежена кривою y=f (x) і прямими х = а, х = b, обчислюється за формулою:
-
 .
. -
-
-
Економічні застосування визначених інтегралів.
