26. Дослідження функції на опуклість, угнутість, точки перегину.

Функція у= f(x) – опукла на деякому проміжку, якщо точки її графіка знаходяться під дотичною.

Якщо над дотичною – угнута.

Теорема ( Достатня ознака опуклості та угнутості)

1. f ( х) > 0 при x є (a,b) f(x) – угнута на (a,b)

2. f ( х) < 0 при x є (a,b) f(x) – опукла на (a,b)

Точкою перегину графіка функції - є точка, яка відокремлює опуклу частину від угнутої.

27. Асимптоти графіка функції.

Види асимптот:

1. Вертикальні ( повязані з наявними точками розриву другого роду).

2. Похилі ( в тому числі горизонтальні)

y = k x+ b – рівняння похилої асимптоти

k =

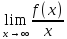
b =

28. Загальна схема дослідження функції та побудови графіка.

1. Глобальне дослідження

1. D (y)

2. Парність, непарність, періодичність.

3. Точки перетину з осями; проміжки знакосталості функції.

4. Дослідження поведінки функції в околі точок розриву та граничних точок області визначення. Вертикальні асимптоти.

5. Поведінка функції при х. Похилі асимптоти.

6. Ескіз графіка за результатами.

ІІ. Локальне дослідження

1. Дослідження на монотонність та екстремуми за допомогою y

2. Дослідження на опуклість, угнутість, точки перегину за допомогою y.

3. Побудова графіка.

29. Знаходження найбільшого та найменшого значення функції на відрізку.

Схема розвязання:

1. D (y); перевірити, що a,b є D (y);

2. y

3. Критичні точки функції f(x).

4. Обрати серед них ті, що належать a,b

5. Обчислити значення f(x) в обраних критичних точках та на кінцяхї відрізка. Висновок.

1. Означення функцій багатьох змінних, графічна, економічна інтерпретація.

Правило f, за яким кожній парі чисел ( х;у) є D ставиться у відповідність єдине число z, назив. Функцією двох змінних, що визначена на множині D.

Z= f( х;у) – позначення.

31. Частинні похідні (означення, механічний та економічний зміст).

Частинна похідна за змінною х від функції Z= f( х;у) – функція, яка одержана при диференцюванні f( х;у) за змінною х у припущенні, що у=const.

32. Повний диференціал функції багатьох змінних.

Розглянемо повний приріст функції: Z= f( х;у)

 Z= f( х+х; у+у) - f( х;у).

Повний диференціал функції Z= f( х;у) знаходиться за формулою, де dz= f_x ( х;у)dx + f_y( х;у)dy він є головною частиною повного приросту функції

dz Z (х0, у0)

33. Градієнт та похідна за напрямом.

Градієнт функції Z= f( х;у) в точці М_о ( х_о; у_о) називається вектор координатами якого є частинні похідні цієї функції в т. М_о.

grad Z М_о = (f_x ( х₀;у₀) ; f_y( х₀;у₀))

Похідна функції Z за напрямом вектора

Формула для обчислення

М_о= grad Z М_о* =

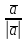
34. Означення та властивості невизначених інтегралів.

Означення. Функція F(x), яка визначена в проміжку (a, b), називається первісною даної функції f(x) в цьому проміжку, якщо для будь-якого значення х(a, b) здійснюється рівність .

Теорема. Будь-яка неперервна функція має безліч первісних, причому будь-які дві з них відрізняються лише на постійну величину.

Означення. Невизначеним інтегралом від даної функції f(x) називається множина усіх її первісних:

де С- довільна стала, . Знак називається знаком невизначеного інтеграла, функція f(x) – підінтегральною функцією, вираз f(x)dx – підінтегральним виразом.

Операція знаходження первісної даної функції називається інтегруванням.

Основні властивості невизначених інтегралів

1)

2)

3)

4)

5),

6) Якщо ,то .

35. Таблиця невизначених інтегралів.

Таблиця основних невизначених інтегралів

1. 

3. 

4. зокрема,

6. 

7. 

8. 

9. 

10. 

11. 

12. Приклади

13. 1).

15. 2) .