10. Дослідження системи лінійних рівнянь на сумісність.

Система m лінійних рівнянь з n невідомими:

Матриця коєфіцієнтів системи:

А=

Розширена матриця

=

Теорема Кронекера- Капеллі:

Система лінійних рівнянь

сумісна тоді і лише тоді, коли ранг розширеної матриці системи дорівнює рангу матриці системи:

r()=r(A)

при цьому:

1.якщо r()=r(A)=n, система визначена

2.якщо r()=r(A)<n, система не визначена

3.якщо r()  r(A), система не сумісна

11. Однорідні системи лінійних рівнянь

Система лінійних рівнянь називається однорідною якщо вона має нульову праву частину.

За рахунок того, що для однорідної системи r()=r(A) ця система завжди сумісна , причому при r()=r(A)=n вона моє лише нульовий розвязок, а при r()=r(A)<n вона має крім нульового- безліч розв’язку.

12. Лінійні дії з векторами.

1.Добуток вектора 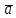на число k- вектор, довжина якого дорівнює, а напрям співпадає з напрямом вектора , якщо k>0 та протележно йому, якщо k<0.

2.Сума двох векторів- це вектор, який визначається за правилом замикання (за правилом трикутника).

3.Різниця векторів- це вектор, який є сумою векторів та . -=+.

13. Означення границі функції, основні властивості.

Означення. Число А називається границею функції y=f(x) при xх₀ якщо для всіх значень х, що достатньо мало відрізняються від числа х₀, відповідні значення функції f(x) як завгодно мало відрізняються від числа А.

Означення. Число А називається границею функції y=f(x) при x+, якщо для всіх достатньо великих значень х відповідні значення функції f(x) як завгодно мало відрізняються від числа А.

Означення границі функції при х- аналогічне.

Іноді буває, що при х + і при х- функція y=f(x) прямує до однієї і тієї ж границі А. Це означає, що для всіх значень х, достатньо великих за абсолютною величиною, відповідні значення y=f(x) як завгодно мало відрізняються від числа А.

Записують це так:

14. Нескінченно малі величини та їх порівняння.

Означення. Функція, яка прямує до нуля при x х₀ , називається нескінченно малою величиною при x х₀. Означення.Якщо -нескінченно малі (при хх0), то (х) і (х) називаються еквівалентними нескінченно малими (при хх₀).

Позначення:

(х)(х) хх₀

15. Нескінченно великі величини та їх порівняння.

Означення. Функція y=f(x) називається нескінченно великою величиною при x х₀, якщо для всіх значень х, що достатньо мало відрізняються від х₀ , відповідні значення функції f(x) за абсолютною величиною перевищують будь-яке наперед задане довільно велике додатне число.

Якщо функція f(x) – нескінченно велика величина при x х₀ , то це записується так:

16. Перша особлива границя та її наслідки.

Перша особлива границя:

Наслідки першої особливої границі:

1)sinxx (x0)

2) tgxx (x0)

3) arcsinxx (x0)

4) arctgxx (x0)

5) 1-cosx  (x0)

17. Друга особлива границя та її наслідки.

Друга особлива границя:

Наслідки другої особливої границі:

1) ln(1+x)x (x0)

2) log(1+x)

3) -1x (x0)

4) -1 x  lna (x0)

5)

6)=e

7)=

18. Таблиця основних еквівалентностей.

1. (x0)

2.tg x x (x0)

3.arcsin x x (x0)

4.arctg x x (x0)

5.1-cos x (x0)

6.ln (1+x)  x (x0)

7.ln y y -1 (x1)

8. (x0)

9.(x0)