Кубічні рівняння

Загальний вигляд кубічного рівняння такий:

.

Поділимо дане рівняння на , дістанемо рівняння

,

старший коефіцієнт якого рівний 1, тобто зведене рівняння.

Нехай дано кубічне рівняння

(1)

з будь-якими комплексними коефіцієнтами.

Щоб позбутися у рівнянні (1) члена з невідомим у другому степені, виконаємо підстановку

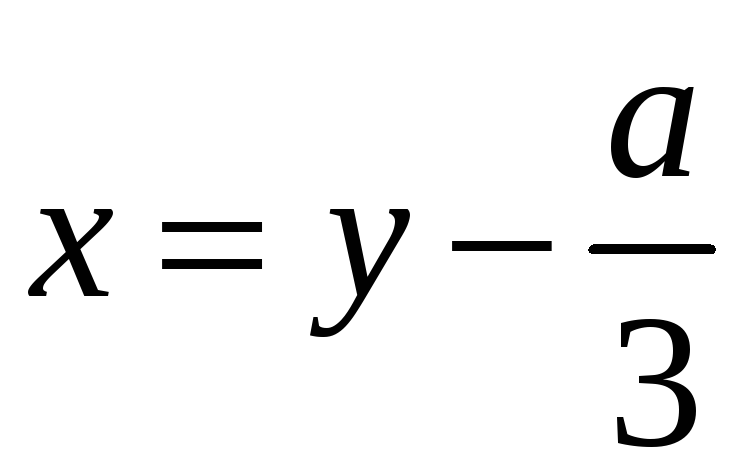
Тоді дістанемо рівняння

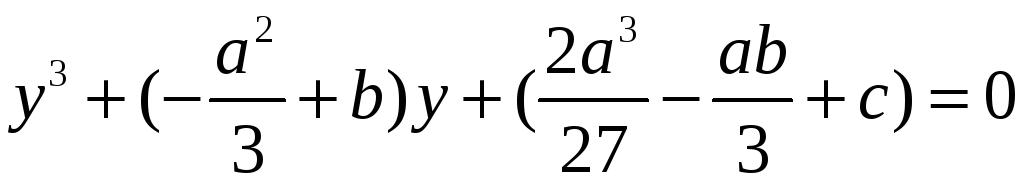(2)

Отже, щоб розв’язати рівняння (1) , досить уміти розв’язувати «неповне» кубічне рівняння

(3)

з будь-якими комплексними коефіцієнтами. Розглянемо один з кількох відомих способів розв’язувати рівняння (3). Запишемо невідоме у вигляді суми , де u і v- нові невідомі, і підставимо цей вираз у рівняння (3).

Дістанемо:

.

Або, після розкриття дужок і перегрупування членів :

.

Якщо u і v вибрати так, щоб

.

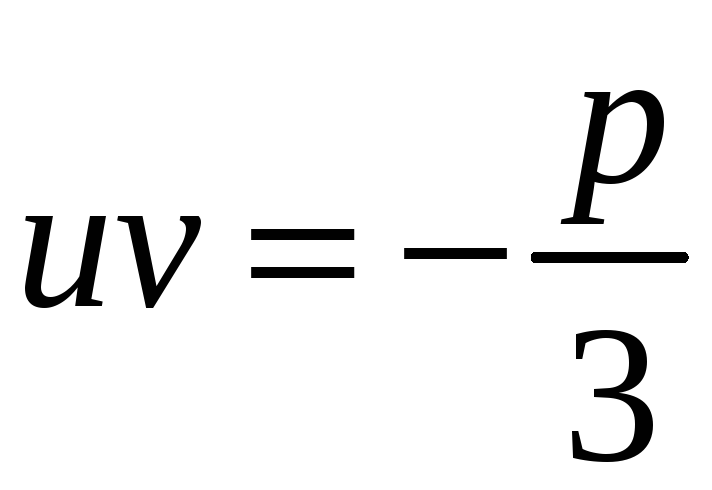(4)

то тоді буде коренем рівняння (3). Але якщо для u і v справджуватимуться рівності (4), то справджуватимуться і рівності

,

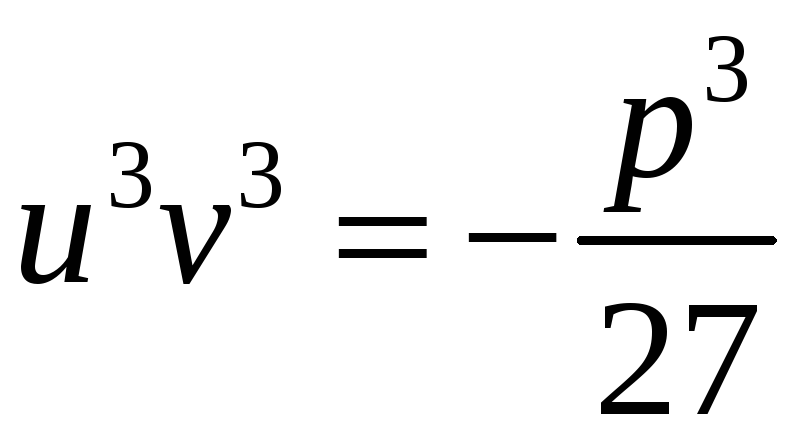(5)

Тому і за формулами Вієта для коренів квадратного рівняння будуть коренями квадратного рівняння

.

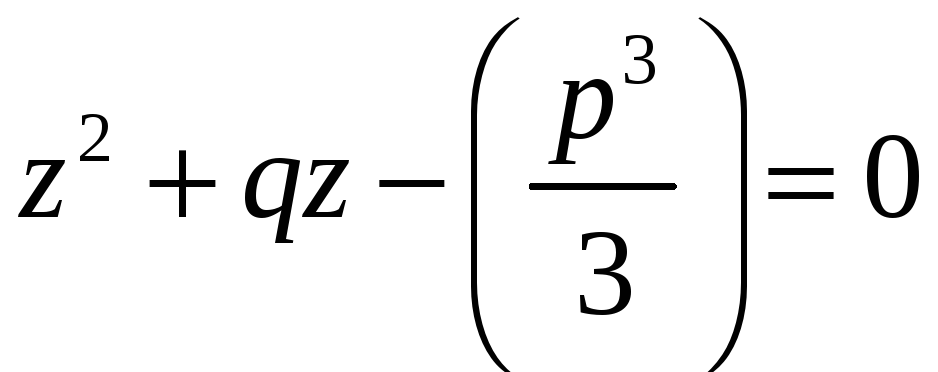Нехай

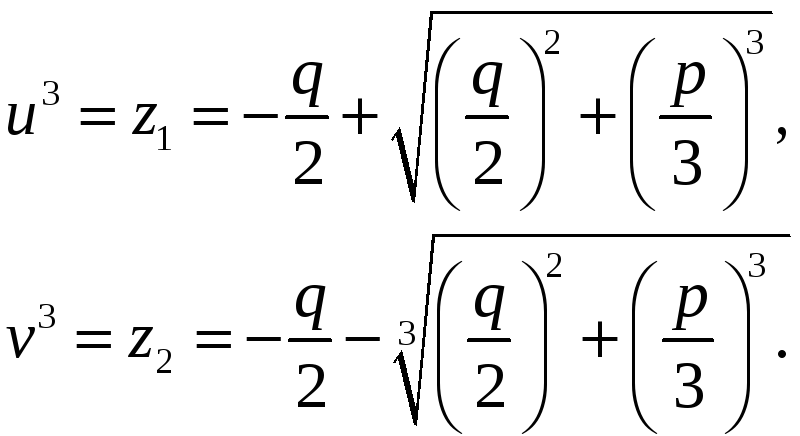
Тоді

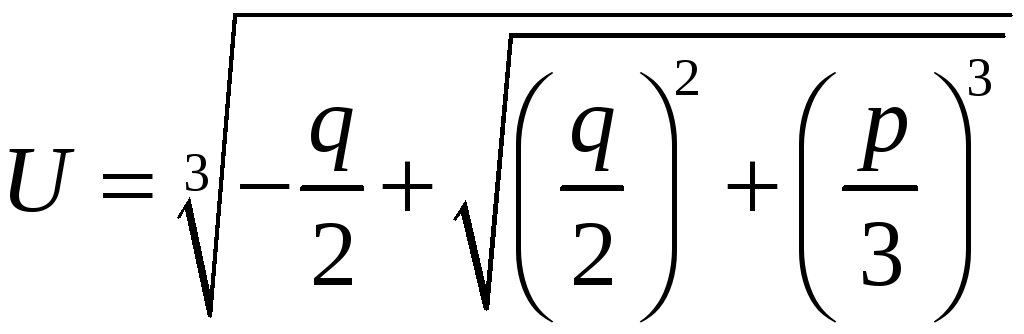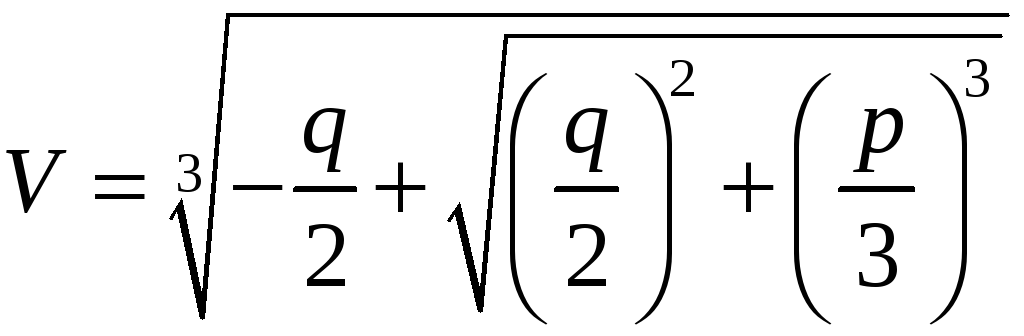, .(6)

Відповідно до цього

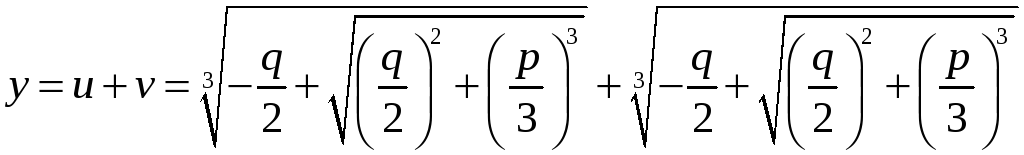(7)

Це і є формула коренів кубічного рівняння, яку називають формулою Кардано.

Кубічний корінь з будь-якого комплексного числа, відмінного від нуля, має в полі комплексних чисел три значення. Отже, і мають по три значення.

Може виникнути думка, що комбінуючи три значення u з трьома значеннями v, дістанемо дев’ять різних значень y за формулою (2)

Проте не слід забувати , що система (5), яку ми фактично розв’язували, не рівносильна системі (4), бо рівність 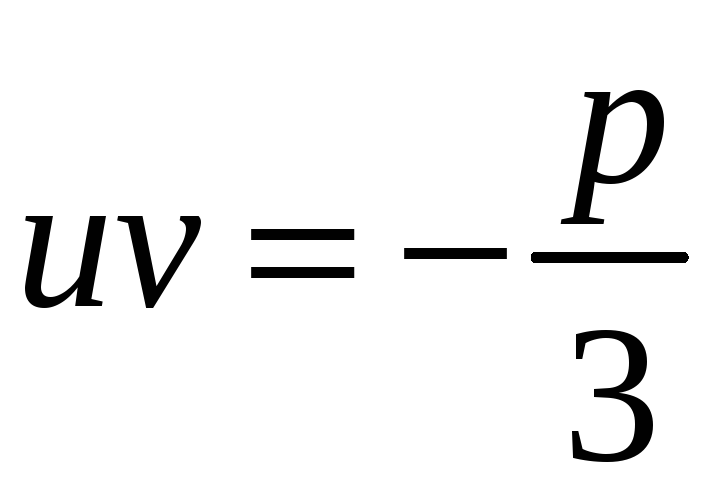замінена рівністю 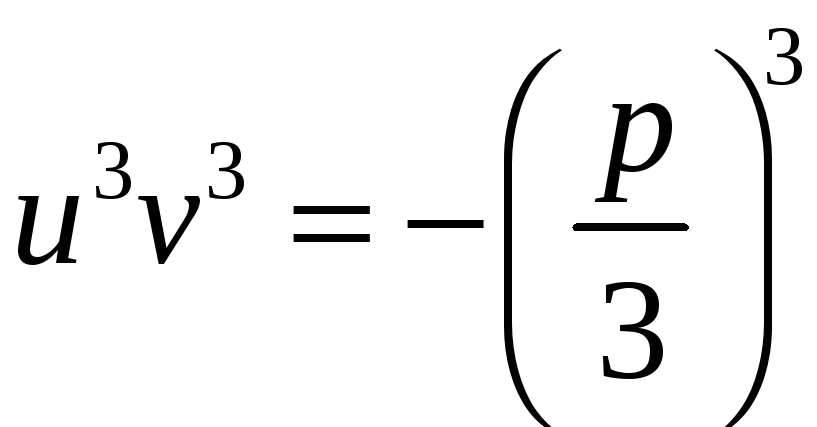. Внаслідок цього не всі розв’язки системи (5) будуть розв’язками системи (4) . Тому слід вибрати лише ті значення коренів (6) , які задовольняють друге з рівнянь (4), тобто умову 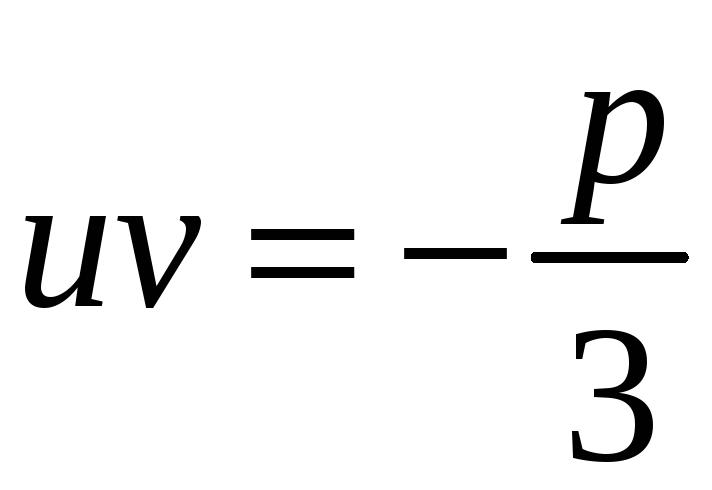(8)

Застосовуючи формулу Кардано, знаходять значення одного з радикалів, а відповідні їм значення другого радикала визначають, користаючи співвідношенням (8), і таким чином, знаходять усі корені рівняння (3).

Спинимося на цьому питанні докладніше.

Нехай - будь-яке одне з трьох значень u . Тоді два інших значення u можна дістати множенням на кубічні корені і з одиниці.

Отже : , , де

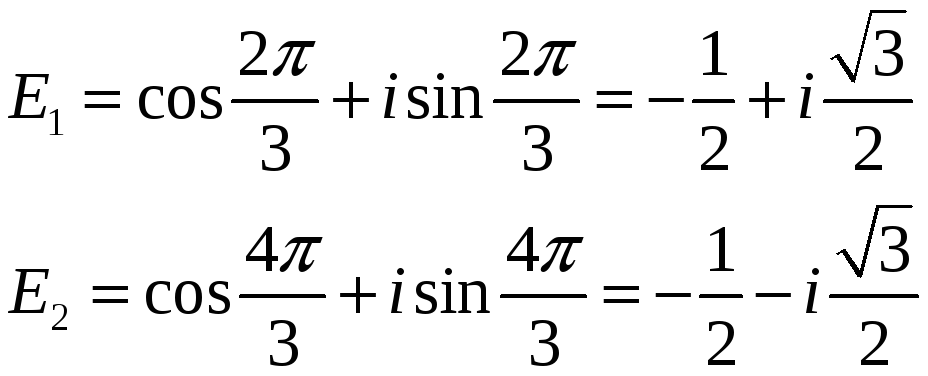
Позначимо символом те з трьох значень радикала V , яке відповідає значення радикала u.

із співвідношення (8):

.

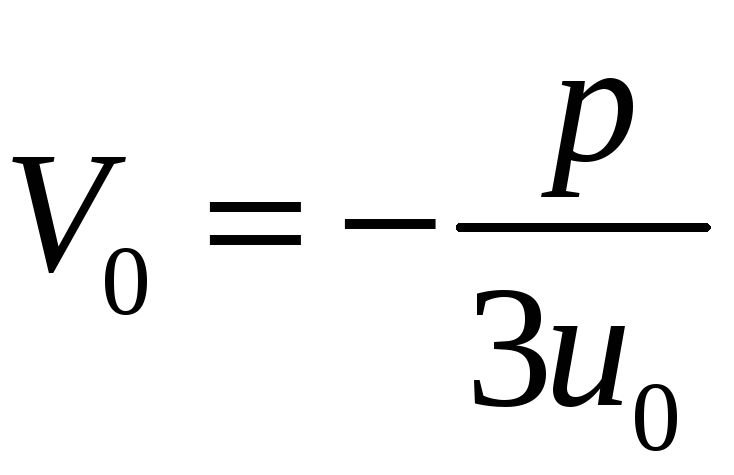Двома іншими значеннями V будуть і . Значенню відповідатиме значення радикала , бо .

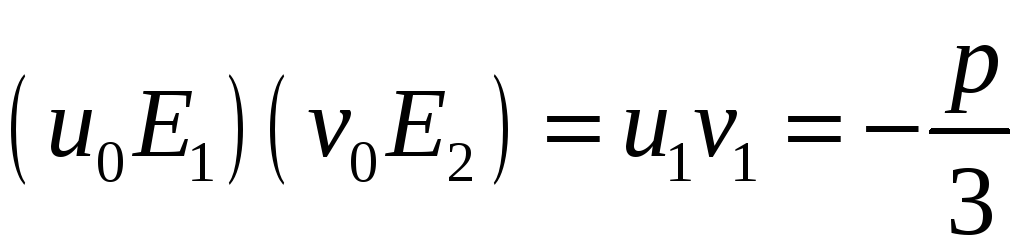Так само легко переконатися , що значення радикала відповідатиме значення радикала V . Додаючи відповідні значення і , дістанемо три корені рівняння (2)

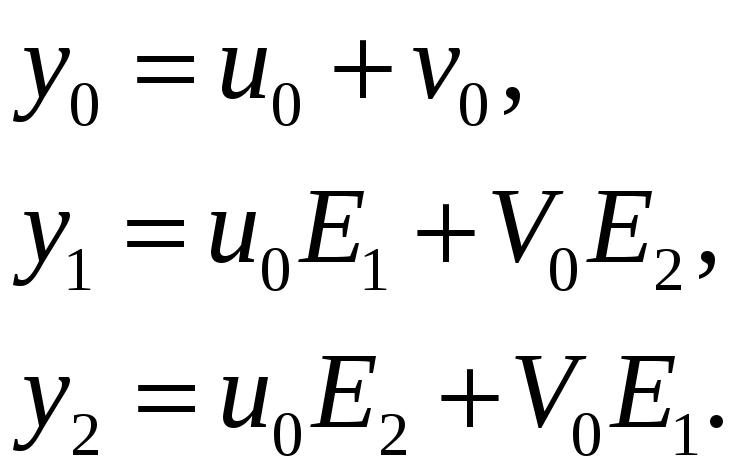(9)

Отже, кожне кубічне рівняння з будь-якими числовими коефіцієнтам в полі комплексних чисел має три корені.

Кубічні рівняння з дійсними коефіцієнтами в полі комплексних чисел

Нехай дано неповне кубічне рівняння:

(10)

з дійсними коефіцієнтами. З’ясуємо, що можна сказати про корені цього рівняння. У цьому випадку вираз 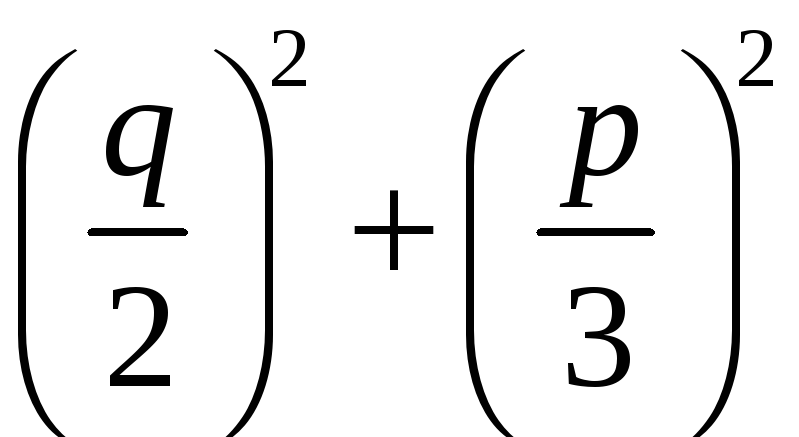, що стоїть у формулі Кардано під знаком квадратного кореня, є дійсне число. Вираз 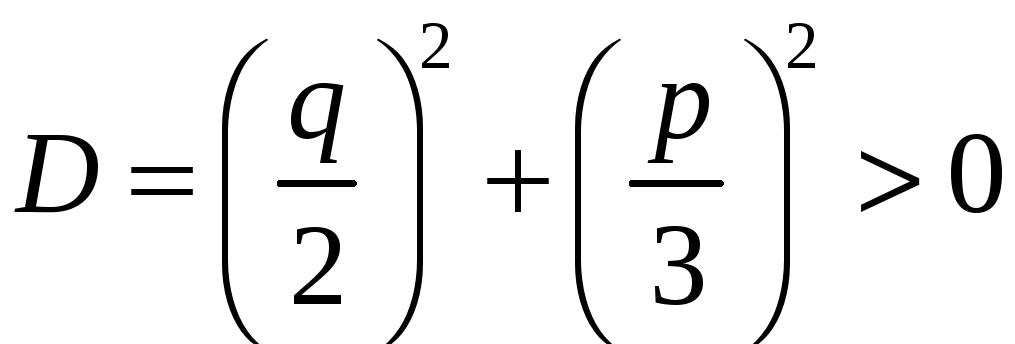називається дискримінантом кубічного рівняння. (10). Цей дискримінант може бути додатним, дорівнювати нулю або бути від’ємним. Розглянемо кожну з цих можливостей.

1.Нехай 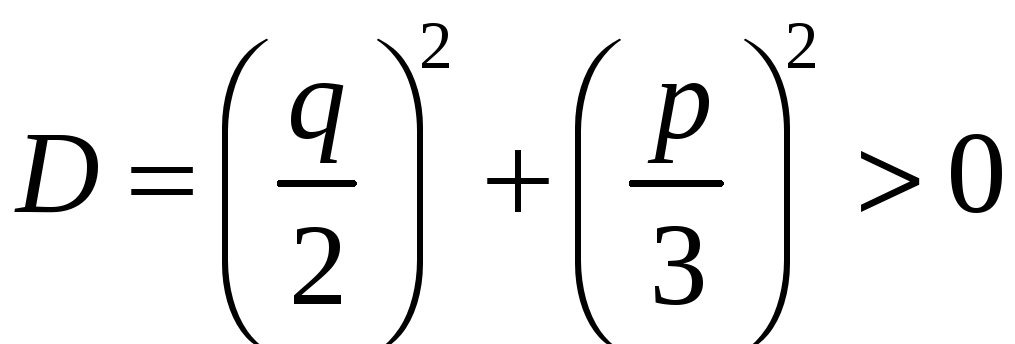. У цьому випадку у формулі Кардано під знаком кожного з квадратних коренів стоїть додатне число, а тому під знаком кожного з кубічних коренів стоїть дійсне число. Отже, кожен з кубічних коренів u і v матиме одне дійсне значення й два –комплексні спряжені.

Позначимо символом дійсне значення радикала u. Тоді відповідне йому значення радикала v також буде дійсним, оскільки добуток повинен дорівнювати .

Таким чином корінь

Рівняння (10) буде дійсним числом. Два інші корені цього рівняння знайдемо за формулами (9):

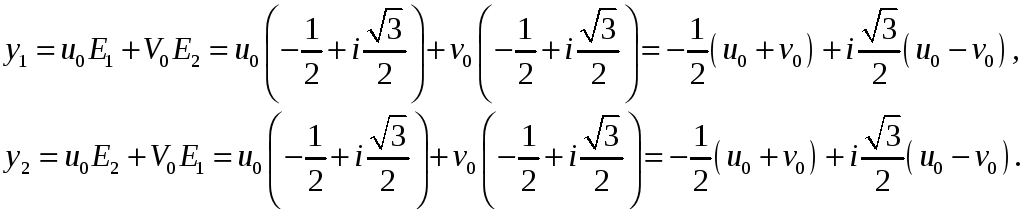Оскільки є дійсні значення різних кубічних радикалів, то ,

і таким чином , корені є спряженими комплексними числами.

Отже, якщо 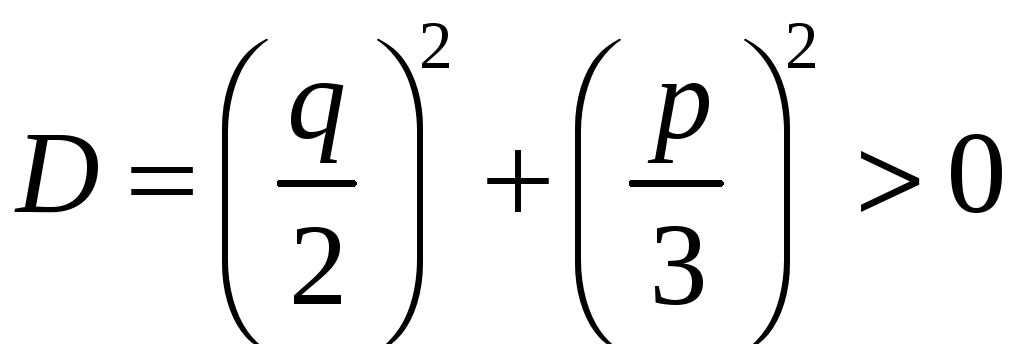то рівняння (10) має один дійсний і два комплексні спряжені корені.

2.Нехай 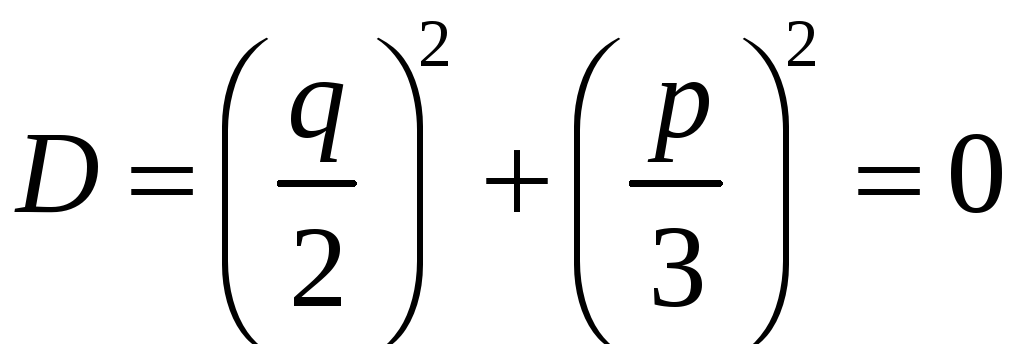.У цьому випадку

, .

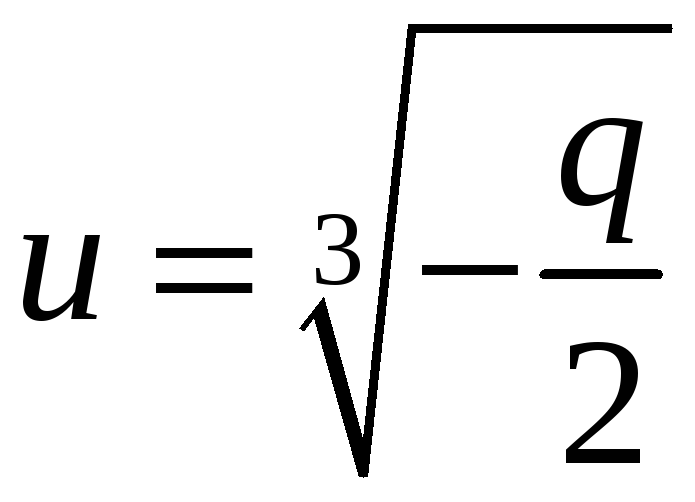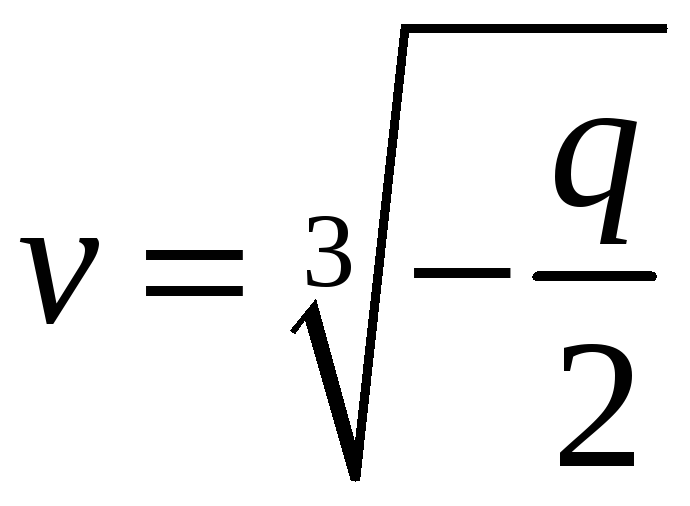Нехай – дійсне значення радикала U . Відповідні йому значення радикала V також є дісним числом, бо . Але оскільки

має лише одне дійсне значення , то . Тому

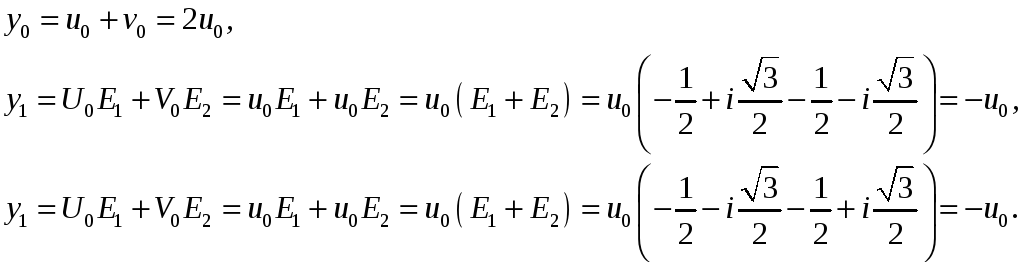Отже, якщо 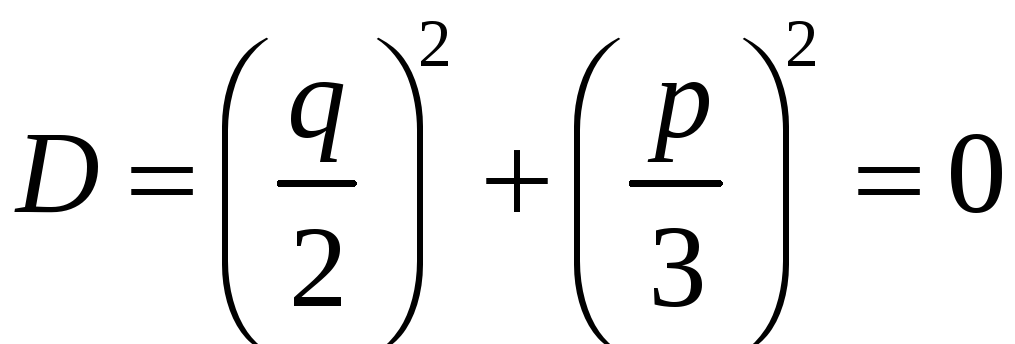, то всі корені рівняння (10) дійсні, причому два з них рівні між собою.

3.Нехай 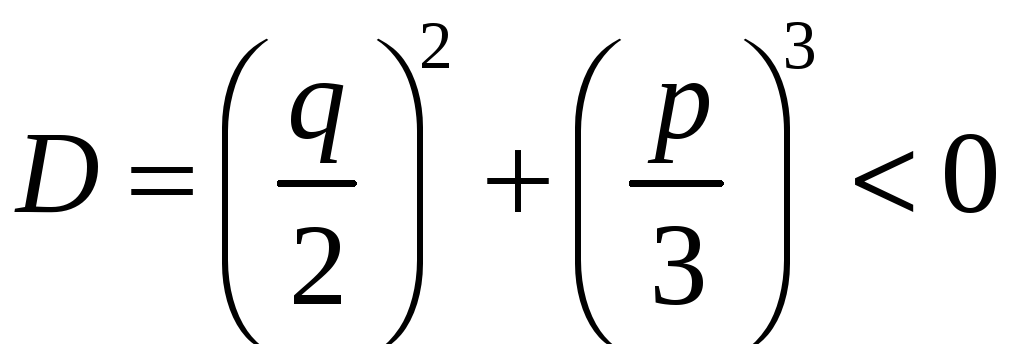. У цьому випадку в формулі Кардано під знаком кожного з квадратних радикалів стоїть дійсне від’ємне число. Отже, під знаком кубічних радикалів стоятимуть u і v стоятимуть комплексні числа, а тому всі значення радикалів u і v будуть комплексними числа.

Покажемо, що в цьому випадку у формулі Кардано значення радикала v повинно бути спряжене відповідному значенню радикала u . Нехай - ,будь-яке із значень радикала u, а відповідне йому значення радикала v. Тоді відповідно до правила добування кореня n-го степеня:

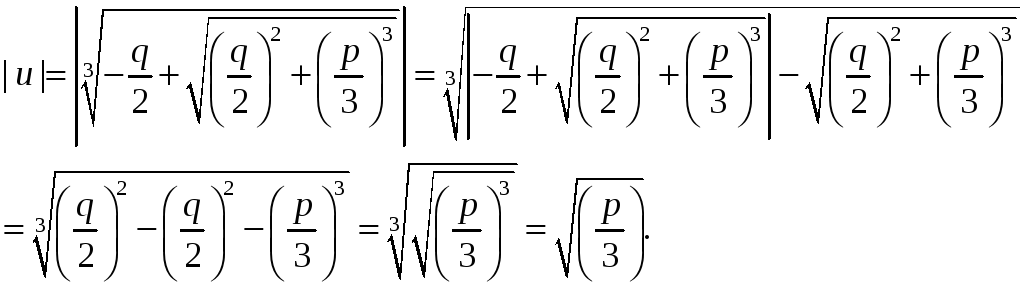і тому

.

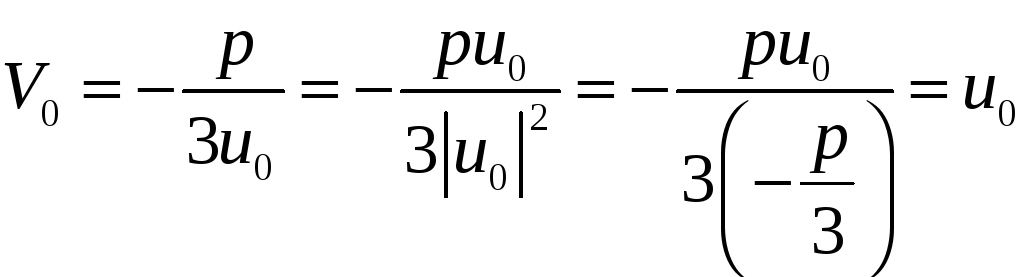Тобто

Таким чином, за формулами (9)

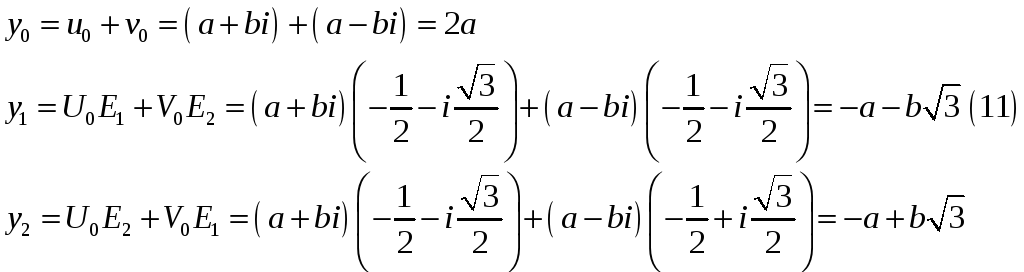Як бачимо, у цьому випадку рівняння (10) має три різні дійсні корені.

Останній випадок переконливо доводить, що практична цінність формули Кардано невелика. Справді, хоч у цьому випадку всі корені рівняння з дійсними коефіцієнтами дійсні, проте відшукання їх за формулою Кардано вимагає добування кубічного кореня з комплексного числа, для чого треба записувати ці числа в тригонометричній формі. Отже, запис коренів кубічного рівняння за допомогою радикалів втрачає практичне значення .

Приклад. Розв’язати рівняння .

Розв’язання

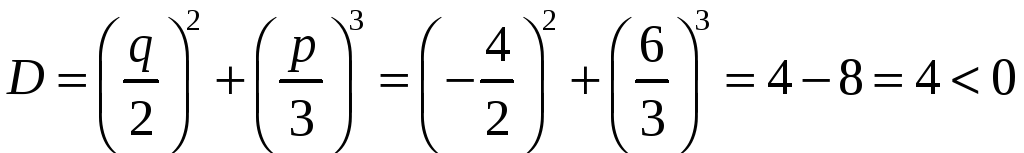
Отже, ми маємо незвідний випадок. Радикал у цьому випадку записується так:

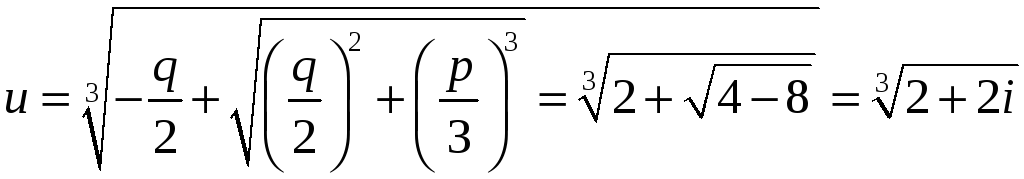
Щоб добути кубічний корінь з комплексного числа , запишемо це число в тригонометричній формі. Знайдемо його модуль ρ і його аргумент γ:

.

, .

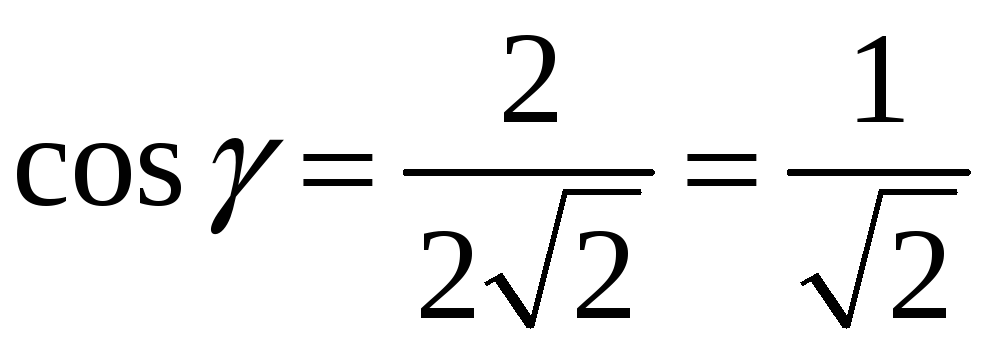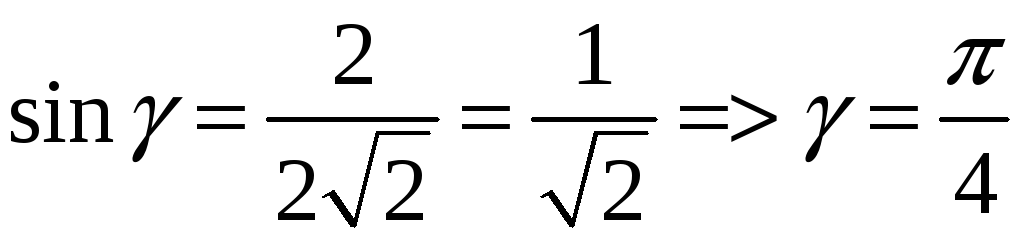
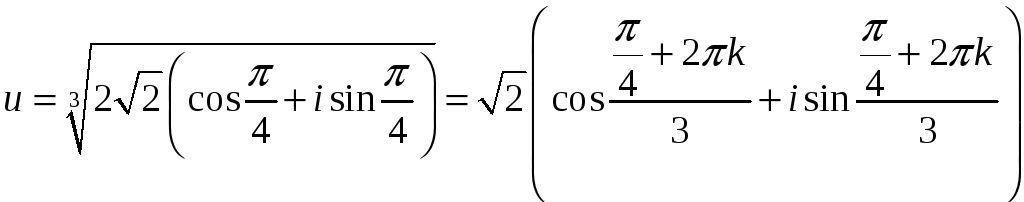
Звідси

.

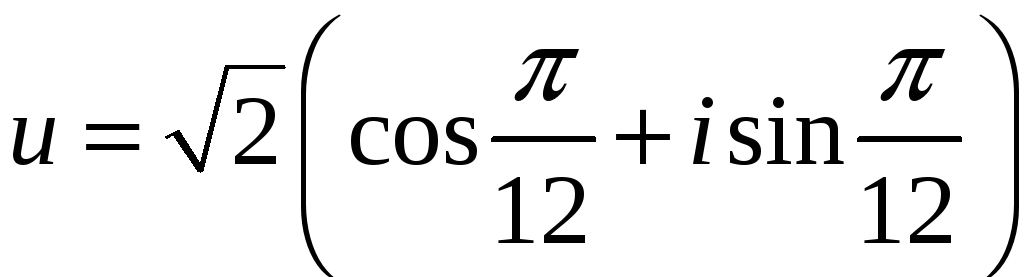І за формулами (6)

.

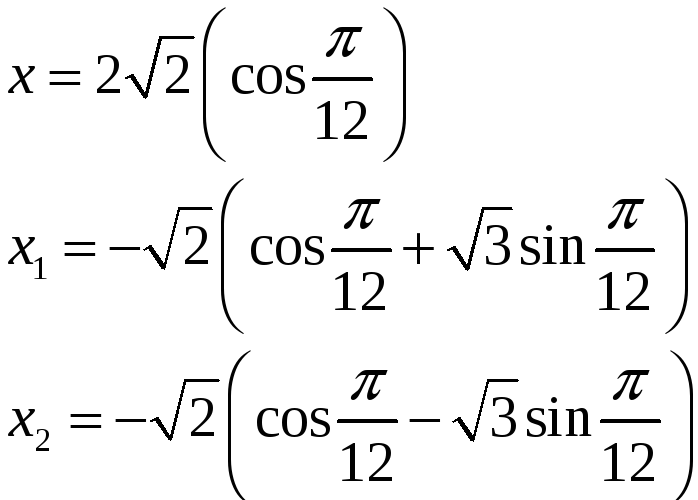Застосовуючи формули ділення аргументу пополам, знаходимо:

.

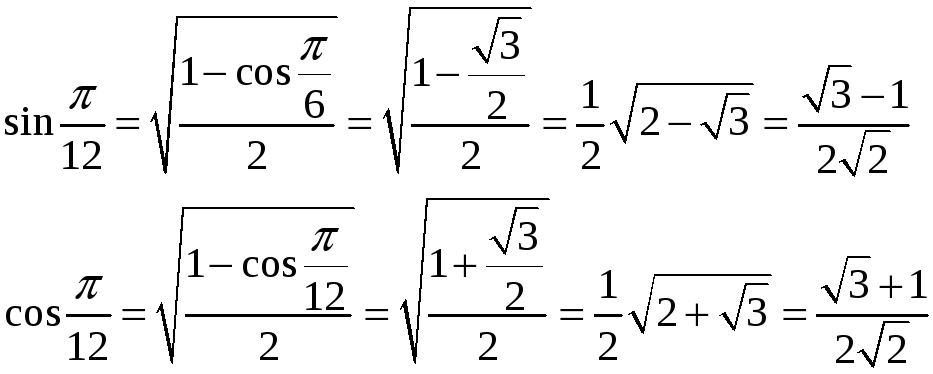Підставивши знайдені значення і у записані вище рівності, матимемо:

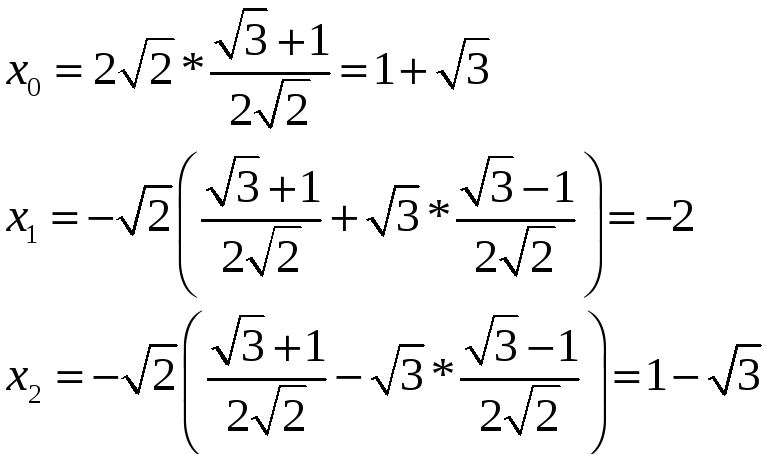
Відповідь: .

Приклад 2. Розв’язати рівняння .

Приклад 3.Розв’язати рівняння .

Приклад 4. Розв’язати рівняння

Розв’язання:

Підстановка зводить рівняння до виду:

.

Тут .

Тобто дане рівняння має один дійсний корінь і два комплексні спряжені:

,

.

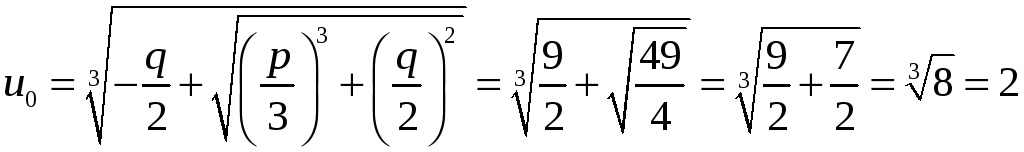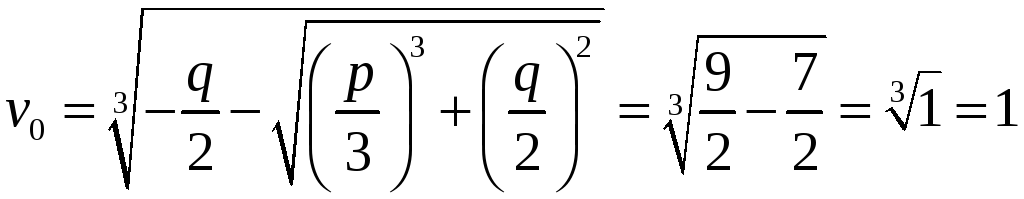Тоді .

Два інших корені знайдемо за формулою (9)

.

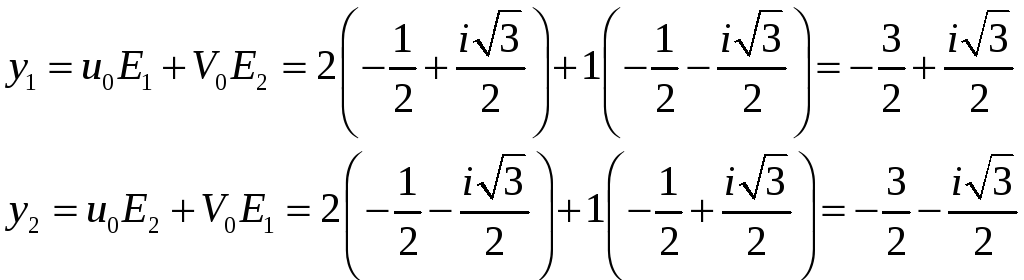У відповідності з підстановкою, знаходимо:

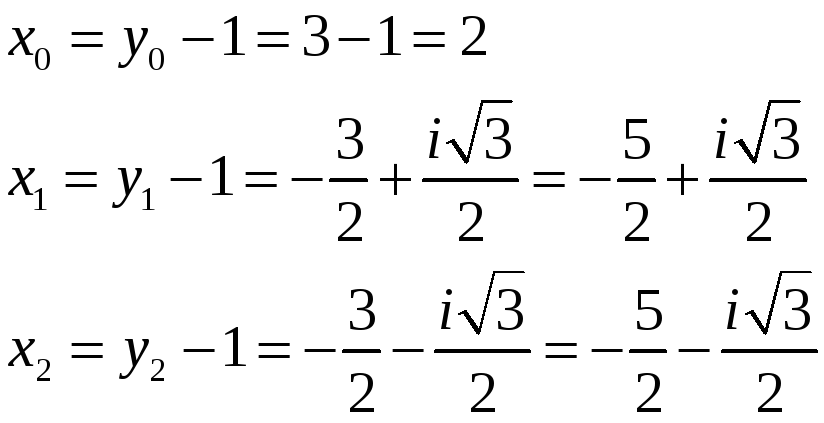
Відповідь: .

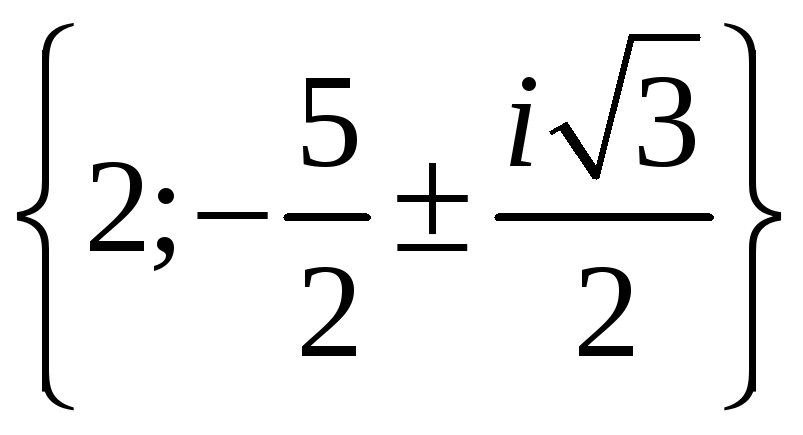Задачі рекомендовані для розв‘язання аудиторії

1. Знайти раціональні корені многочленів:

а) ;

б) ;.

в) ;

г) ;

д) .

2. Розв’язати рівняння:

а) ; б) .

в) ; г) .

д) ; е) ;

є) ; ж) .

Задачі рекомендовані для розв‘язання дома

1. Знайти раціональні корені многочленів:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

2. Розв’язати рівняння:

а) ; б) ;

в) ; г) .

д) ; е) ;

є) ; ж) .

85