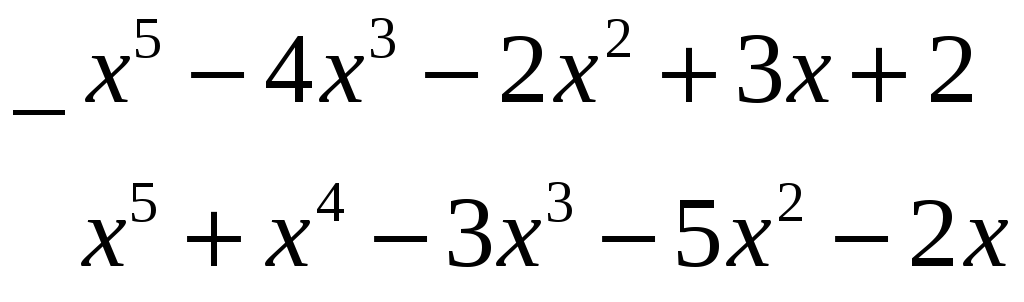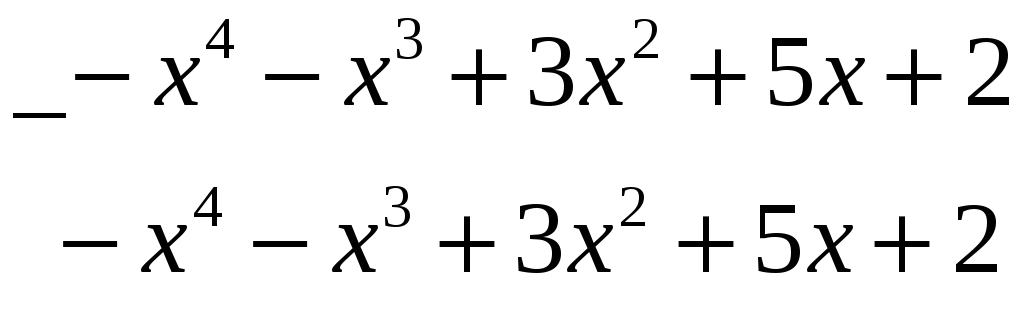Основні теоретичні відомості
Ми
знаємо, що всякий многочлен над полем![]() можна єдиним способом подати у вигляді
добутку многочленів нижчих степенів,
незвідних у полі:
можна єдиним способом подати у вигляді
добутку многочленів нижчих степенів,
незвідних у полі:
![]() (1)
(1)
Вивчати властивості многочленів, знаходити їх корені було б значно легше, якби для кожного многочлена був відомий канонічний розклад (1), тоді було б досить розглядати лише незвідні множники, степінь яких, як правило, значно нижчий за степінь даного многочлена.
Покажемо, як в даних випадках можна розробити загальний метод розкладання многочлена на множники, хоч цей розклад не буде таким повним, як зображено у (1).
Виберемо
у розкладі (1) ті незвідні множники
![]() кратність
яких
кратність
яких
![]() і позначимо добуток цих множників через
і позначимо добуток цих множників через
![]()
![]()
Далі
утворимо добуток тих множників
![]() кратність яких
кратність яких
![]() і позначимо добуток цих множників через
і позначимо добуток цих множників через
![]()
![]()
Зауважимо,
![]() означає добуток самих незвідних
множників кратності 2, а не їх квадратів,
так що в розклад входить
означає добуток самих незвідних
множників кратності 2, а не їх квадратів,
так що в розклад входить
![]()
Аналогічно
через
![]() позначимо добуток незвідних множників
у розкладі (1), що мають кратність 3, і так
далі.
позначимо добуток незвідних множників
у розкладі (1), що мають кратність 3, і так
далі.
Тоді розклад (1) можна записати у такому вигляді:
![]() (2)
(2)
або
спрощено:
![]() (3)
(3)
Якщо
множників кратності
![]() у розкладі (1) немає, природно вважати
у розкладі (1) немає, природно вважати
![]()
Задача зображення многочлена у вигляді (2) називається виділенням кратних множників.
Теорема
14.
Якщо незвідний у даному полі
![]() многочлен
многочлен
![]() є множником кратності
є множником кратності
![]() для многочлена
для многочлена
![]() то він є множником кратності
то він є множником кратності
![]() для похідної
для похідної
![]()
Якщо
![]() є множником першої кратності многочлена
є множником першої кратності многочлена
![]() то він не входить у розклад похідної
то він не входить у розклад похідної
![]() на незвідні множники.
на незвідні множники.
Наслідок.
Для того, щоб многочлен
![]() не мав кратних множників, необхідно і
достатньо, щоб
не мав кратних множників, необхідно і
достатньо, щоб
![]() був взаємно простий із своєю похідною
був взаємно простий із своєю похідною
![]() .
.
Як
ми знаємо будь-який многочлен у даному
полі можна подати у вигляді
![]() (3).
(3).
Наше
завдання полягатиме в тому, щоб, знаючи
лише коефіцієнти
![]() визначити
визначити
![]()
Оскільки
![]() є добутком незвідних множників многочлена
є добутком незвідних множників многочлена
![]() ,
які мають кратність
,
які мають кратність
![]() то в
то в
![]() жодний з цих множників (за теоремою 14)
входити не буде.
жодний з цих множників (за теоремою 14)
входити не буде.
![]() - добуток незвідних множників кратності
- добуток незвідних множників кратності
![]() У
У
![]() усі ці множники входять з кратністю 1,
тобто
усі ці множники входять з кратністю 1,
тобто
![]() має своїм множником
має своїм множником
![]() усіх цих незвідних множників у першому
степені.
усіх цих незвідних множників у першому
степені.
Аналогічно,
якщо
![]() має множником
має множником
![]() то
то
![]() матиме множник
матиме множник
![]()
Таким чином, можемо записати
![]() де
де
![]()
Тоді
за (6)
![]()
Знайдемо
![]()
Аналогічно можна обчислити:
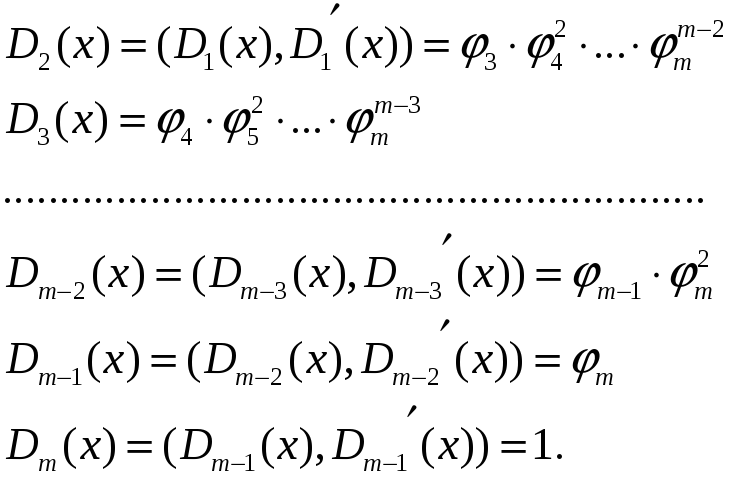 (4)
(4)
![]() вже
не містять непотрібних нам множників
вже
не містять непотрібних нам множників
![]() Наша мета, полягає в тому, щоб знайти
Наша мета, полягає в тому, щоб знайти
![]() окремо.
окремо.
Для
цього поділимо
![]() на
на
![]() Дістанемо:
Дістанемо:
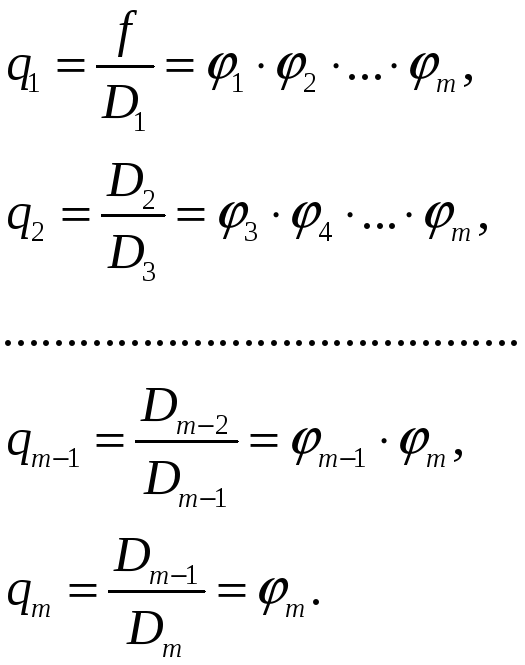 (5)
(5)
Із
(4) і (5) шукані множники
![]() дістаємо безпосередньо:
дістаємо безпосередньо:
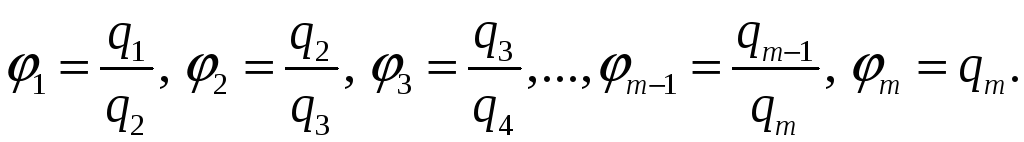 (6)
(6)
Висновок.
У довільного многочлена над полем
![]() можна відокремити кратні множники за
допомогою скінченного числа раціональних
дій над деякими многочленами.
можна відокремити кратні множники за
допомогою скінченного числа раціональних
дій над деякими многочленами.
В
означенні:
[Елемент
![]() називається
називається
![]() -
кратним коренем многочлена
-
кратним коренем многочлена
![]() ,
якщо
,
якщо
![]() але не ділиться на
але не ділиться на
![]() ]
ми
розглянули поняття кореня кратності
]
ми
розглянули поняття кореня кратності
![]() У ряді випадків буває зручно користуватися
ознакою кратності кореня, яку ми
розглянемо як теорему А.
У ряді випадків буває зручно користуватися
ознакою кратності кореня, яку ми
розглянемо як теорему А.
Теорема
А.
Для
того, щоб
![]() був коренем кратності
був коренем кратності
![]() необхідно і достатньо, щоб
необхідно і достатньо, щоб
![]()
Теорема А показує, що, знаючи корінь многочлена, легко визначити його кратність. Тому на практиці дослідження многочленів, які мають кратні корені, у більшості випадків зводить до дослідження многочленів нижчих степенів, що вже не мають кратних коренів. Це завжди можна зробити відокремленням кратних множників методами, описаними вище.
Методичні рекомендації до розв‘язання задач
Приклад 1. Відокремити кратні множники у многочлені
![]()
Розв’язання.
1. Знайдемо спочатку
![]()
![]() і
і
![]()
Застосуємо
алгоритм Евкліда, а також практичний
спосіб для спрощення обчислень
![]()
_
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Далі,
ділимо
![]() на
на
![]()
![]()

![]()
![]()
![]()
![]()
![]()
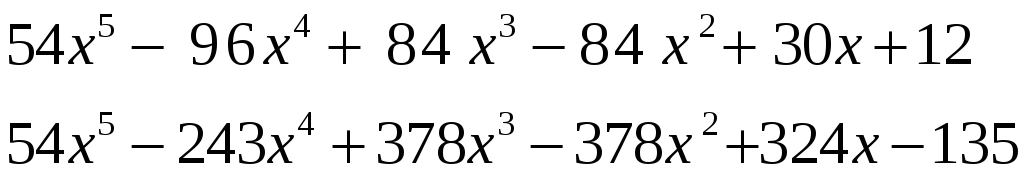
![]()
![]()
![]()
Ділимо
![]() на
на
![]()
![]()

![]()
![]()
![]()

0
![]()
![]()
Ділимо
![]() на
на
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ділимо
![]() на
на
![]()
![]()

![]()
![]()
![]()
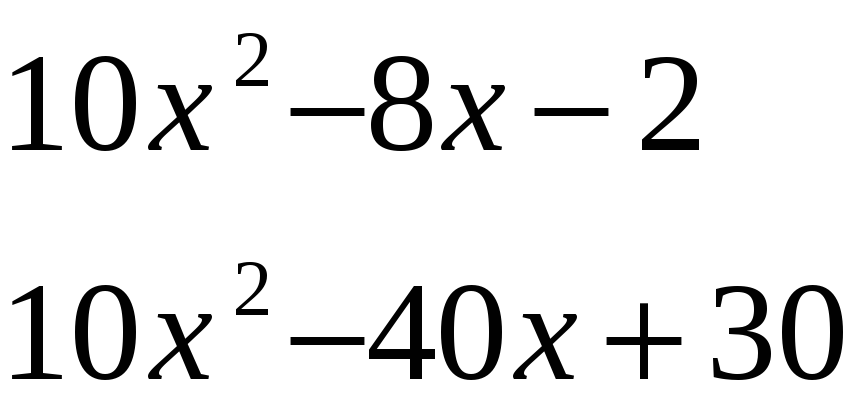
![]()
![]()
![]()
Ділимо
![]() на
на
![]()
![]()

![]()
![]()
![]()
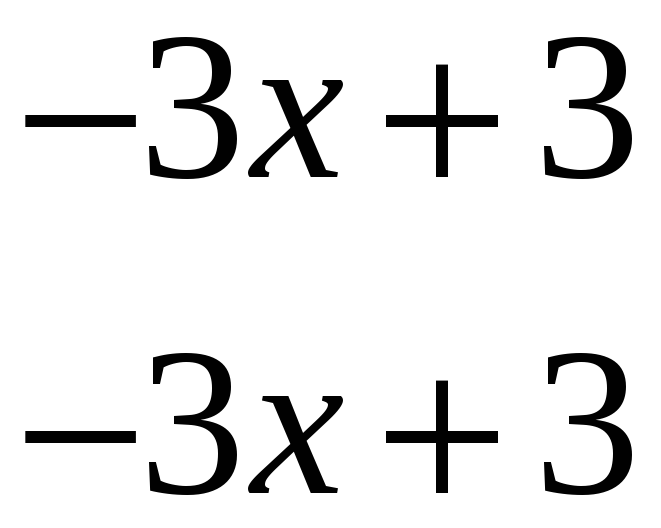
0
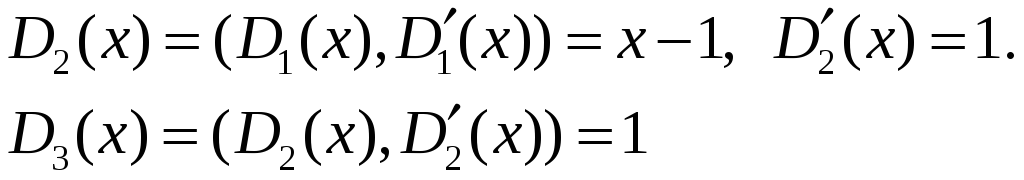
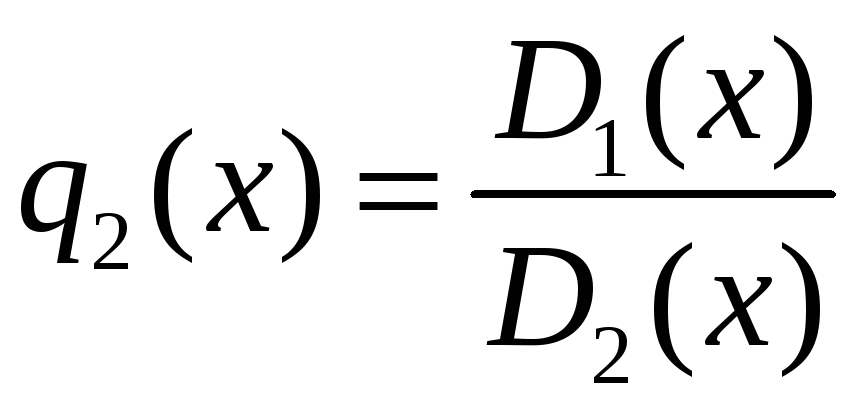
![]()

![]()
![]()
![]()
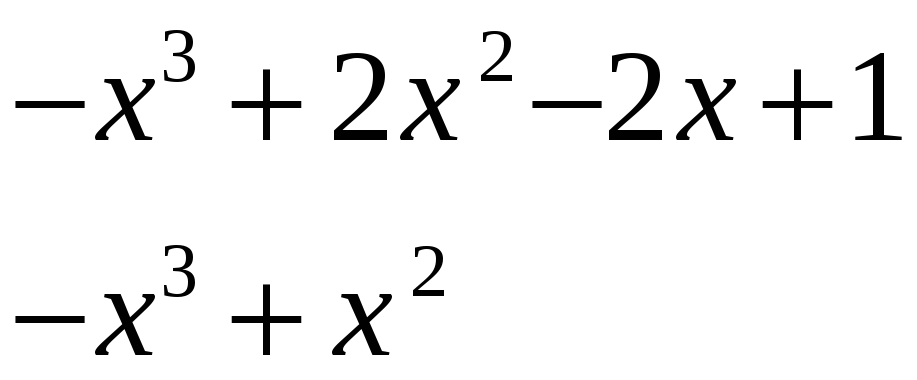
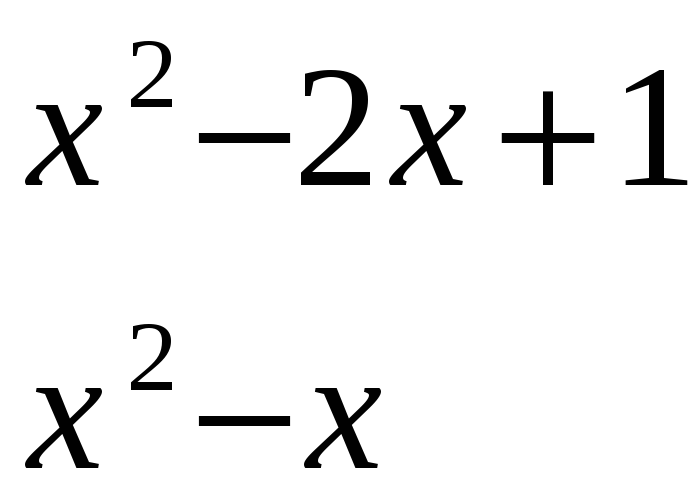
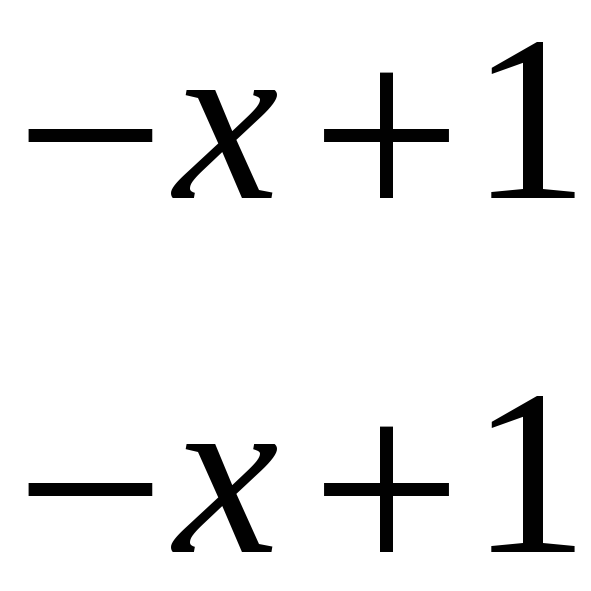
0
![]()
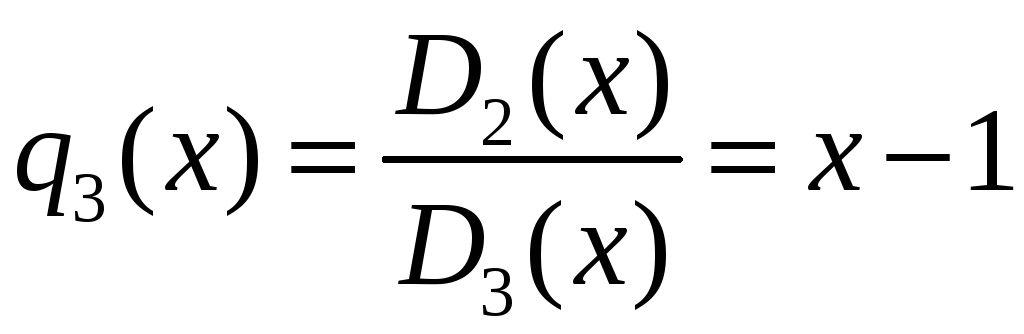
3.
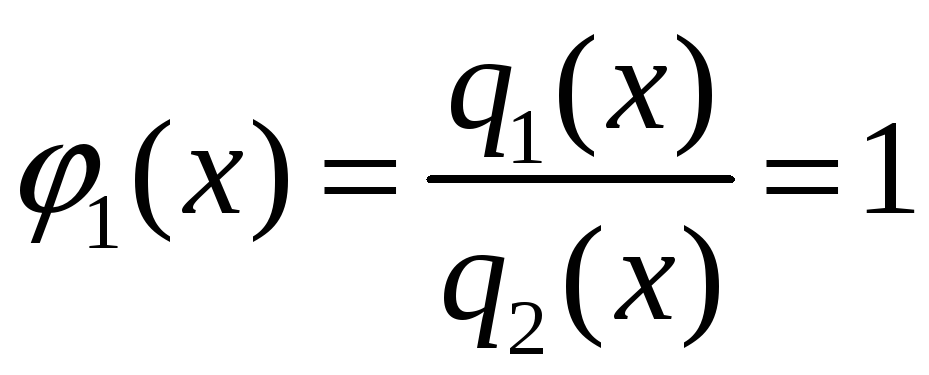 ;
;
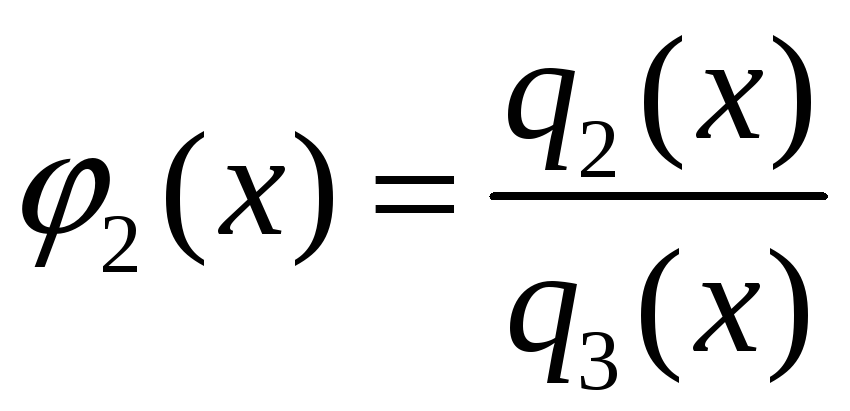 ,
,
![]() ;
;
![]() .
.
![]()
Приклад 2. Відокремити кратні множники многочлена
![]()
Розв’язання.
Знаходимо
![]() і
і
![]() .
.
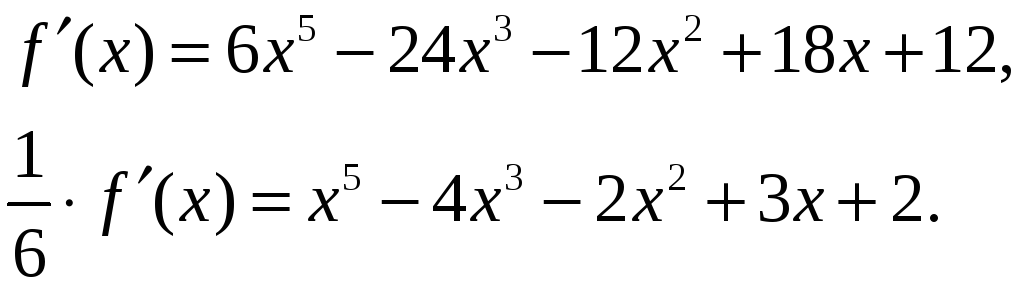
|
|
|
|
|
|
|
|
(ділимо на 2)
|
|
|
|
|
|
|
|
|
|
|
Отже,
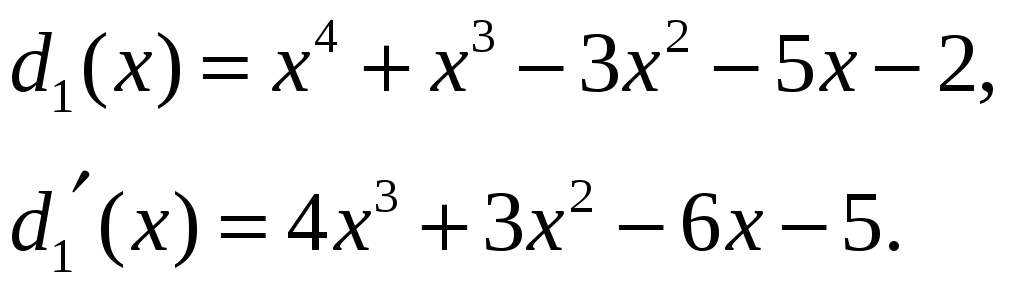
Аналогічно знаходимо:
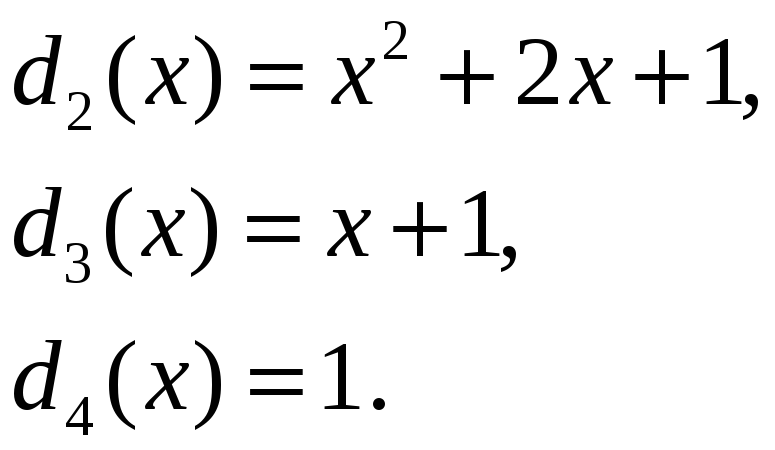
Обчислимо
тепер
![]()
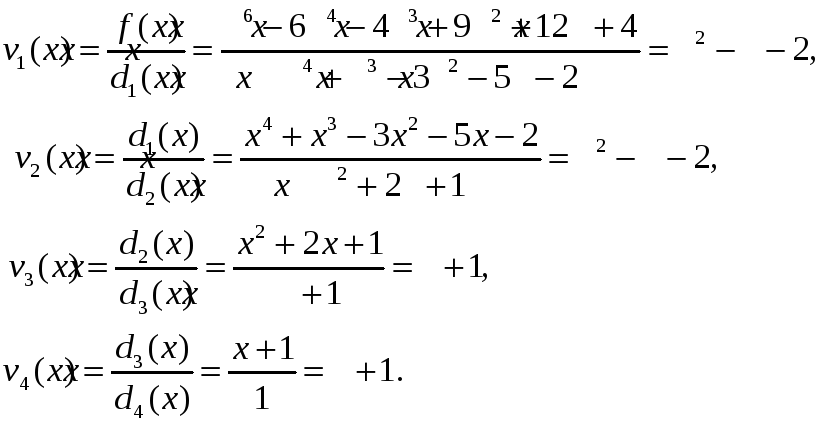
Шукані многочлени дорівнюють:
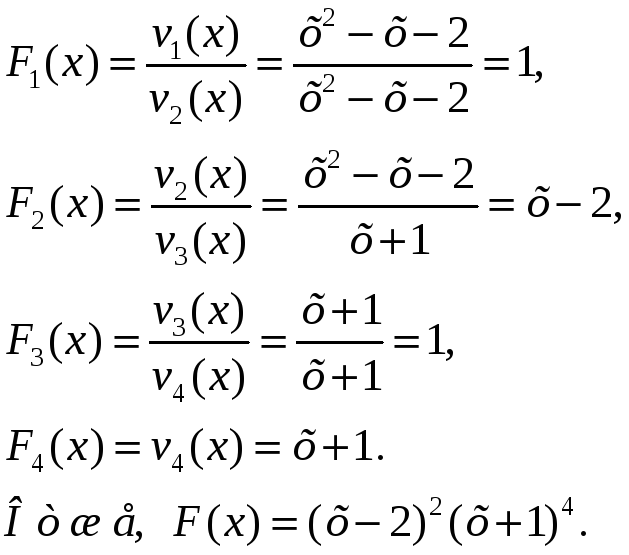
Приклад 3. Відокремити кратні корені многочлена
![]()
Розв‘язання.
![]()
Тут
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Многочлен
![]() має
прості корені
має
прості корені
![]() і 3-х
кратний корінь – 2.
і 3-х
кратний корінь – 2.
Отже,
![]()
![]()
![]() .
.![]()
![]()
Задачі рекомендовані для розв‘язування в аудиторії
Відокремити кратні множники многочленів:
1.
![]()
2.
![]()
3.
![]()
4.
![]() .
.
Задачі рекомендовані для розв‘язування дома
Відокремити кратні множники многочленів:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]() .
.
Модуль 4
Практичне заняття 4
Розклад раціональних дробів на елементарні
Основні теоретичні відомості
Для
будь-якого поля
![]() існує (з точністю до ізоморфізму) поле
існує (з точністю до ізоморфізму) поле
![]() ,
яке містить кільце
,
яке містить кільце
![]() многочленів над полем
многочленів над полем
![]() і кожен елемент якого можна подати як
частку
і кожен елемент якого можна подати як
частку
![]() ,
де
,
де
![]() . (1)
. (1)
Зауважимо,
що відповідно до загальної теорії
елементом поля
![]() є не кожна окрема частина (1), а клас
часток, які дорівнюють одна одній.
є не кожна окрема частина (1), а клас
часток, які дорівнюють одна одній.
Дві
частки
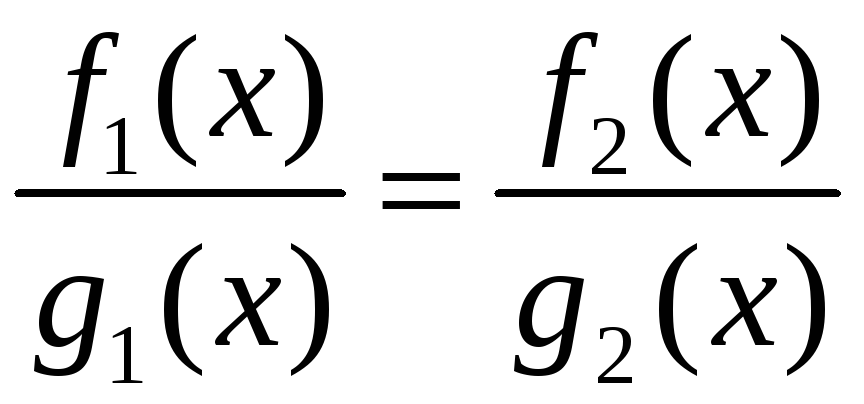 дорівнюють одна одній, якщо
дорівнюють одна одній, якщо
![]() .
Як правило, раціональний дріб подають
часткою
.
Як правило, раціональний дріб подають
часткою
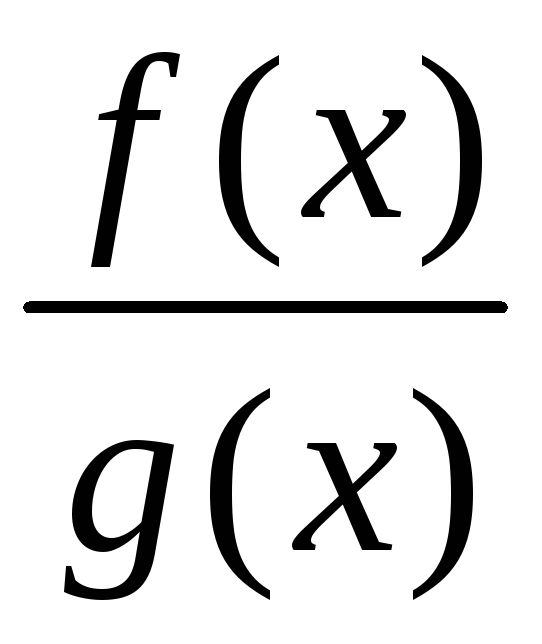 ,
для якої
,
для якої
![]()
Нехай раціональні дроби задано нескоротними частками і старший коефіцієнт знаменника дорівнює 1.
Раціональний
дріб
![]() називається правильним,
якщо степінь
називається правильним,
якщо степінь
![]() менше степеня
менше степеня
![]() .
У противному разі раціональний дріб
називається неправильним.
.
У противному разі раціональний дріб
називається неправильним.
Елементарним
дробом
над полем
![]() називається раціональний дріб виду
називається раціональний дріб виду
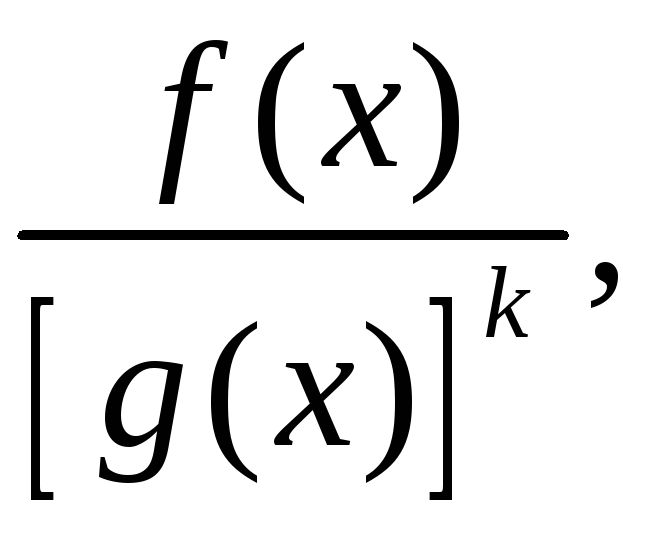 де
де
![]() - незвідний многочлен над полем
- незвідний многочлен над полем
![]() ,
,
![]()
Якщо
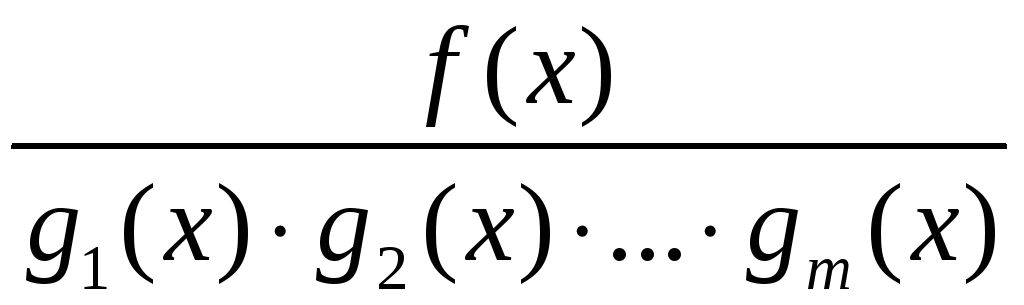 - правильний раціональний дріб над полем
- правильний раціональний дріб над полем
![]() і многочлени
і многочлени
![]() - попарно взаємно прості, то в кільці
- попарно взаємно прості, то в кільці
![]() існують многочлени
існують многочлени
![]() такі, що
такі, що
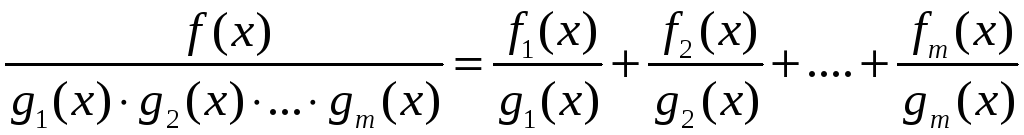
і кожен з дробів у правій частині є правильним.
Правильний
дріб над полем
![]() виду
виду
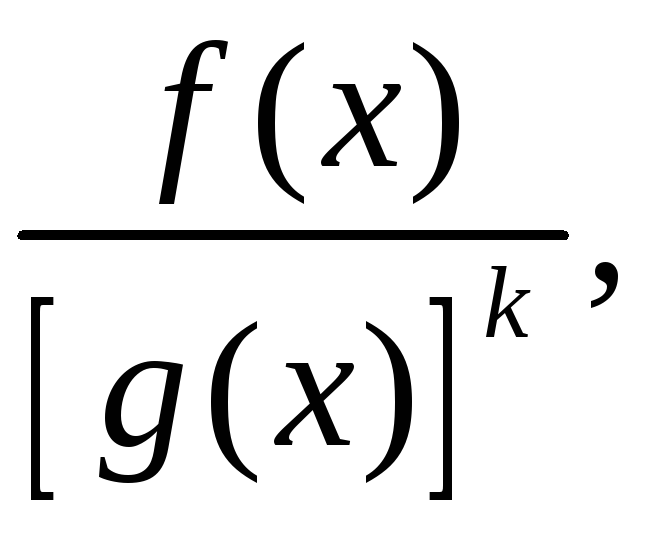 де
де
![]() - незвідний над
- незвідний над
![]() многочлен і
многочлен і
![]() можна подати як суму елементарних дробів
над цим полем.
можна подати як суму елементарних дробів
над цим полем.
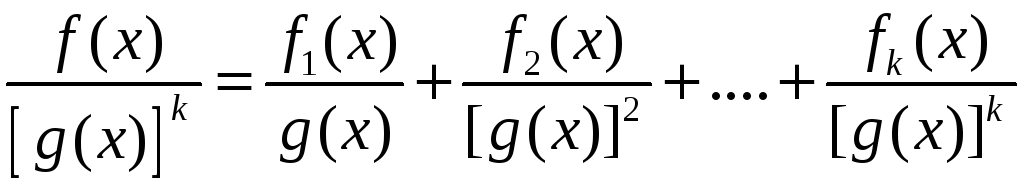 .
.
Правильні
дроби над полем
![]() можна подати як суму елементарних дробів
над цим полем і до того єдиним способом.
можна подати як суму елементарних дробів
над цим полем і до того єдиним способом.
Неправильний
дріб
![]() можна подати як суму многочлена і
правильного дробу.
можна подати як суму многочлена і
правильного дробу.
Основна теорема теорії многочленів
Теорема. Довільний многочлен ненульового степеня з комплексними коефіцієнтами
![]()
має хоча б один комплексний корінь.
Методичні рекомендації до розв’язування задач
Приклад
1.
Розкласти в суму простіших дробів
дійсний правильний дріб
![]() ,
де
,
де
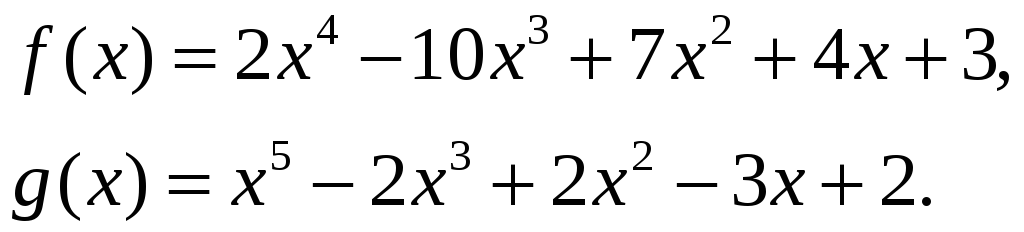
Легко
перевірити, що
![]() причому кожний із многочленів
причому кожний із многочленів
![]() незвідний. Шуканий розклад повинен мати
вигляд
незвідний. Шуканий розклад повинен мати
вигляд
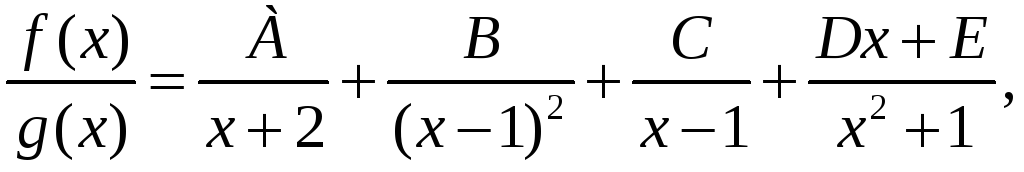 (1)
(1)
де
числа
![]() треба ще знайти.
треба ще знайти.
Многочлен
![]() можна розкласти:
можна розкласти:
![]()
![]() (2)
(2)
Прирівнюючи
коефіцієнти при однакових степенях
невідомого
![]() із обох частин рівності (2), ми отримали
б систему із п’яти лінійних рівнянь
відносно п’яти невідомих
із обох частин рівності (2), ми отримали
б систему із п’яти лінійних рівнянь
відносно п’яти невідомих
![]() ,
при чому, ця система має рішення і притому
лише одне. Ми підемо, однак, іншим шляхом.
,
при чому, ця система має рішення і притому
лише одне. Ми підемо, однак, іншим шляхом.
Нехай
у рівності (2)
![]() ,
тоді маємо, що
,
тоді маємо, що
![]() звідки
звідки
![]() (3)
(3)
Ставлячи
, в (2)
![]() ,
ми отримаємо
,
ми отримаємо
![]() ,
тобто
,
тобто
![]() (4)
(4)
Після
цього підставимо в рівність (2) послідовно
![]() Використовуючи (6) і (7), ми отримаємо
рівняння
Використовуючи (6) і (7), ми отримаємо
рівняння
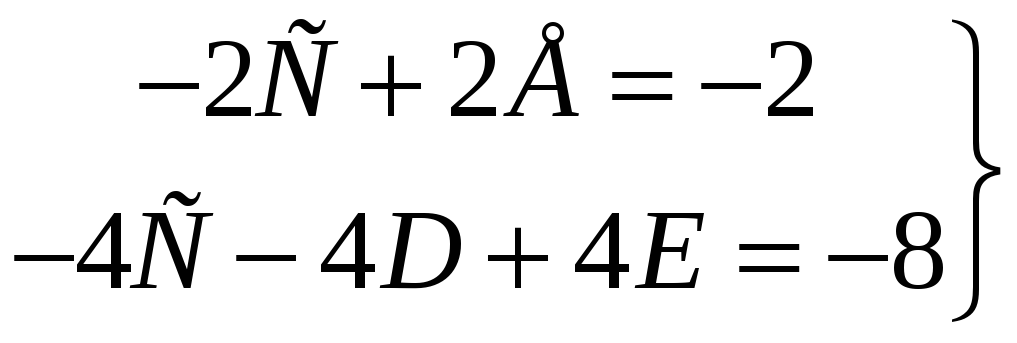 (5)
(5)
Звідси
![]() (6). Підставимо в рівність (2)
(6). Підставимо в рівність (2)
![]() Використовуючи (3), (4) і (5), ми прийдемо
до рівняння
Використовуючи (3), (4) і (5), ми прийдемо
до рівняння
![]() яке разом з першим із рівнянь (8) дає
яке разом з першим із рівнянь (8) дає
![]()
Таким чином,
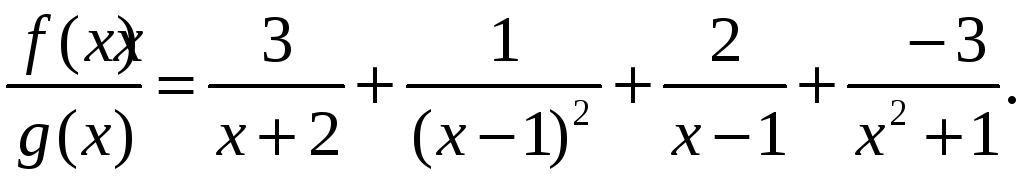
Задачі рекомендовані до розв‘язування в аудиторії
І.
Розкладіть вирази на прості дроби над
полем
![]()
1.
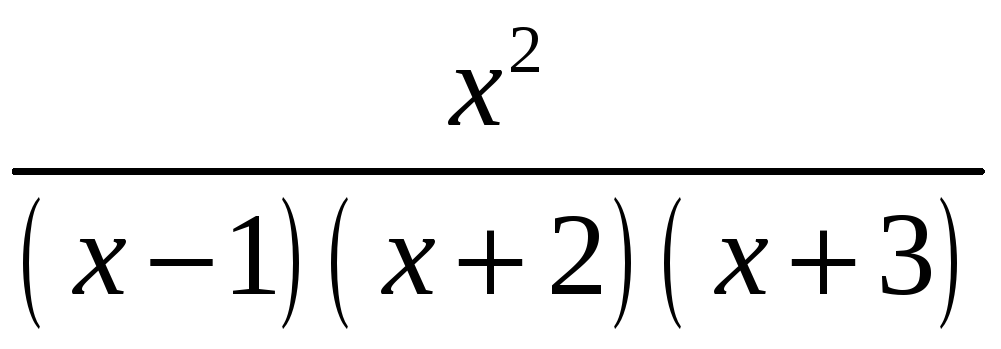 ;
2.
;
2.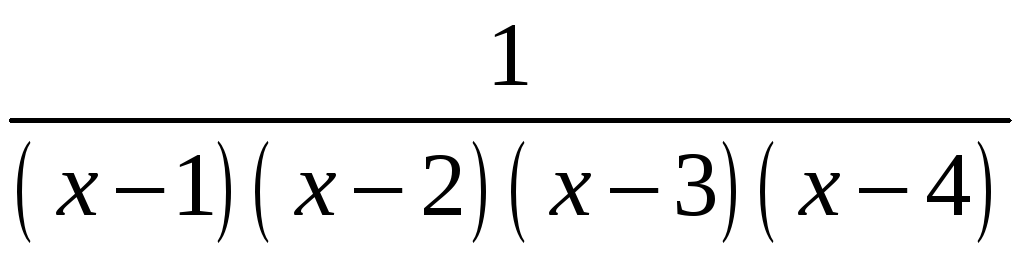 ;
;
3.
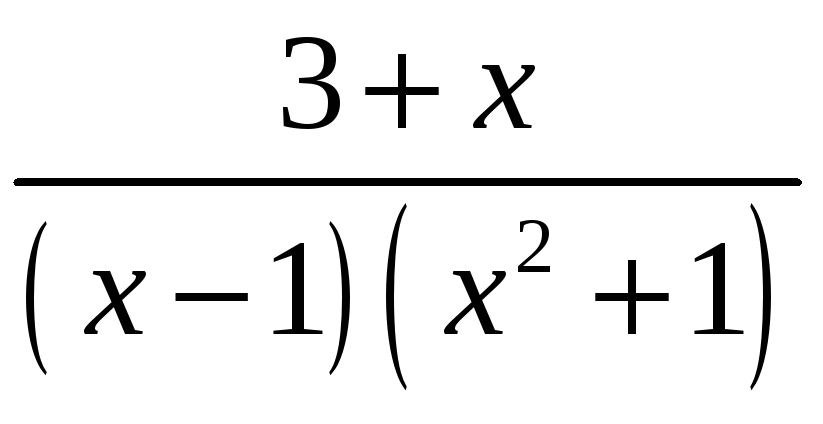 ;
4.
;
4.
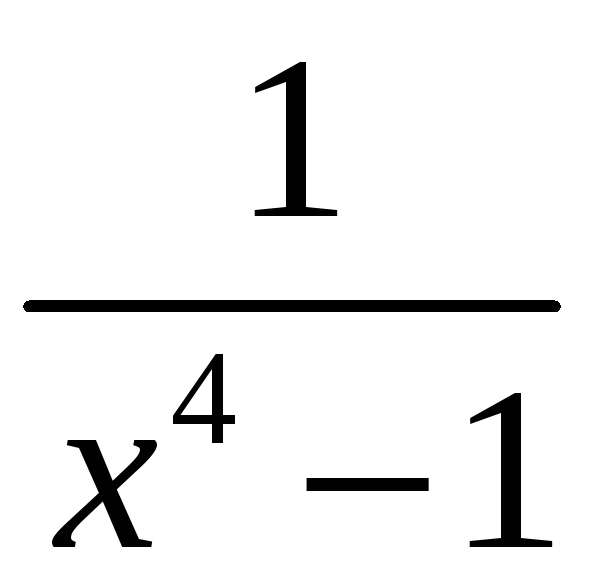 ;
;
5.
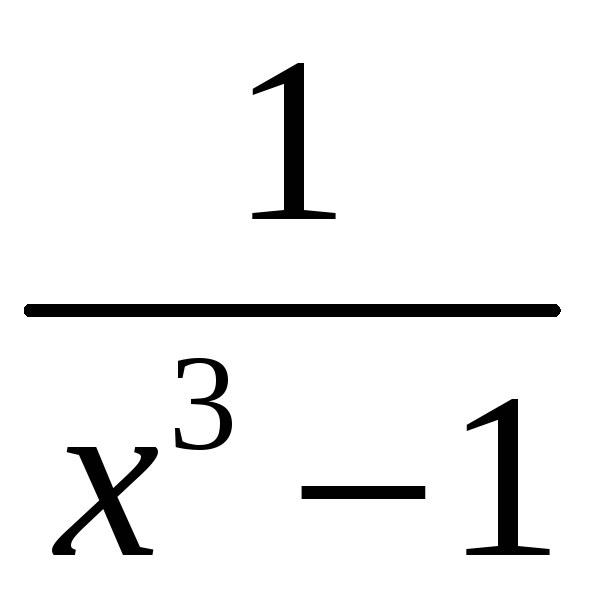 ;
6.
;
6.
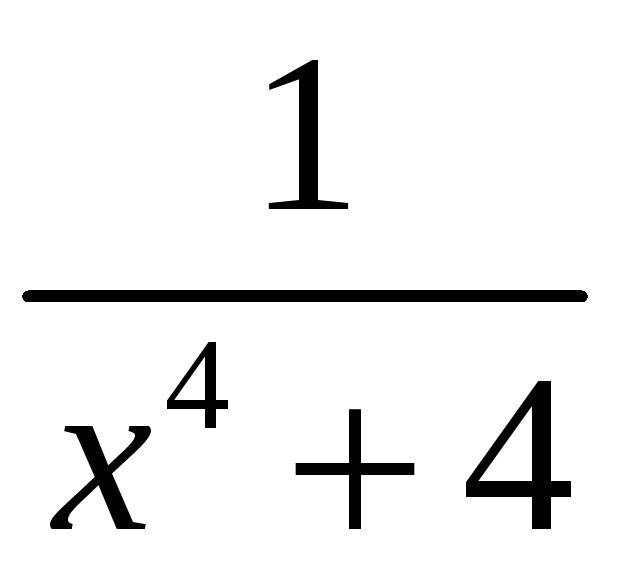 ;
;
7.
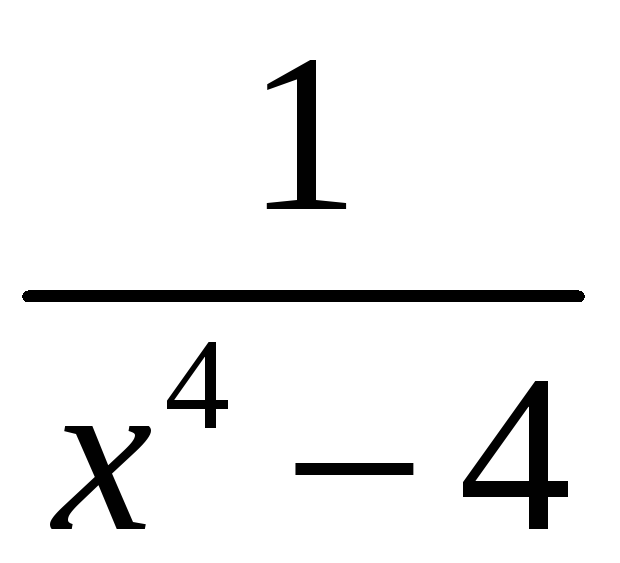 ;
8.
;
8.
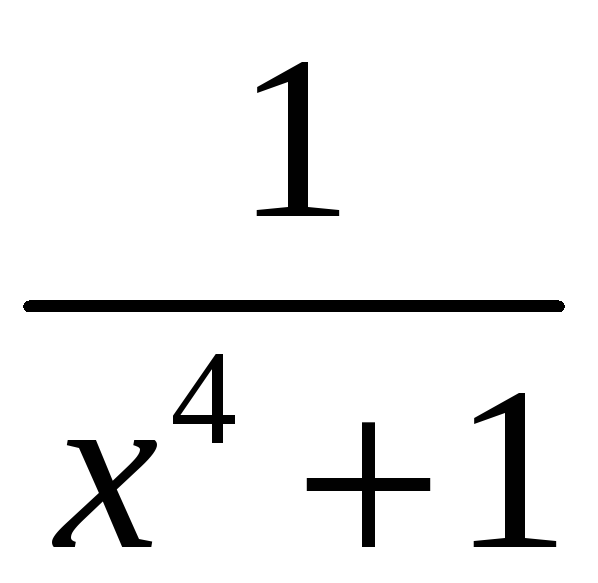 ;
;
9.
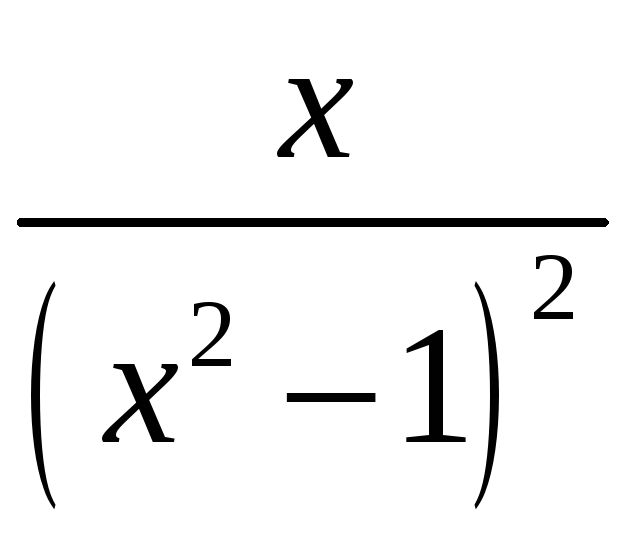 ;
10.
;
10.
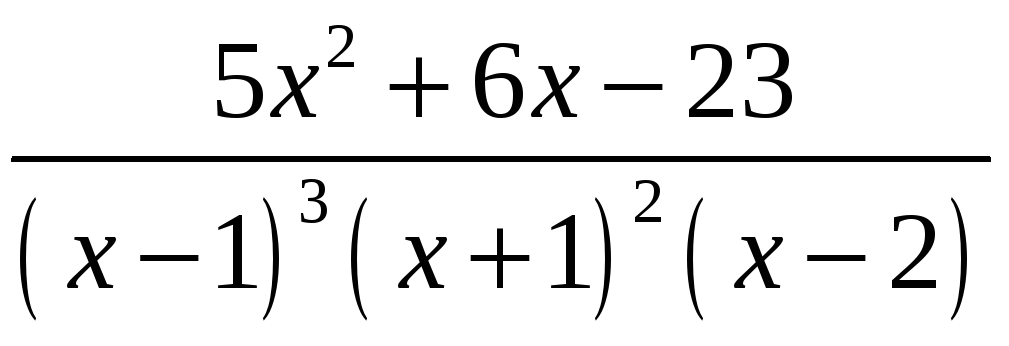 .
.
Задачі рекомендовані до розв‘язування в аудиторії
І.
Розкладіть вирази на прості дроби над
полем
![]()
1.
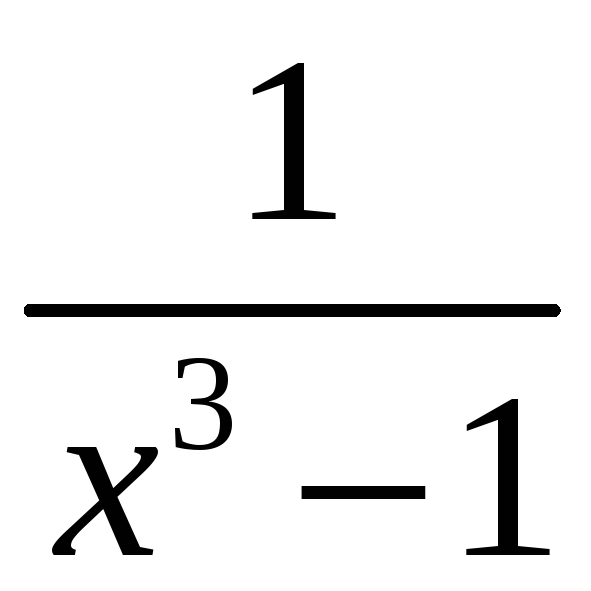 ;
2.
;
2.
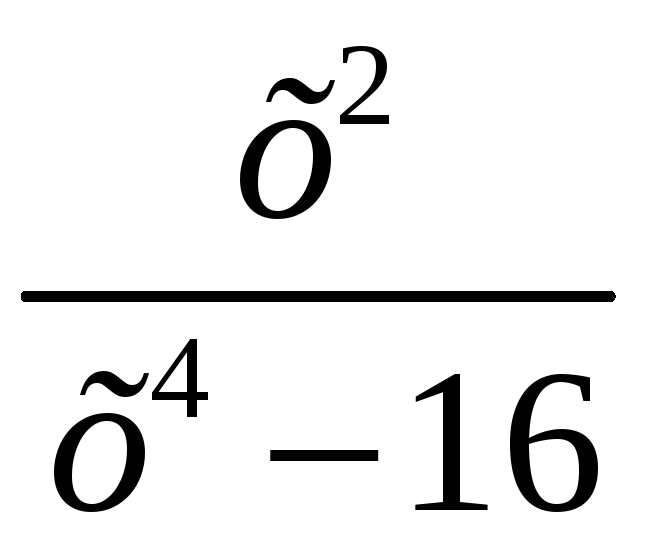 ;
;
3.
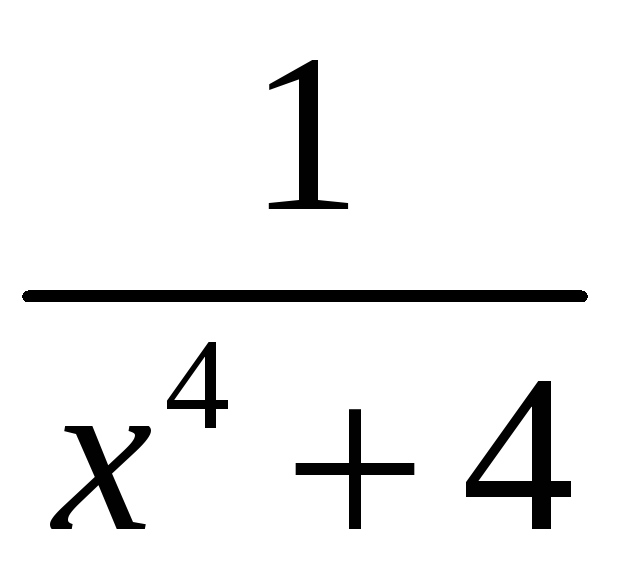 ;
4.
;
4.
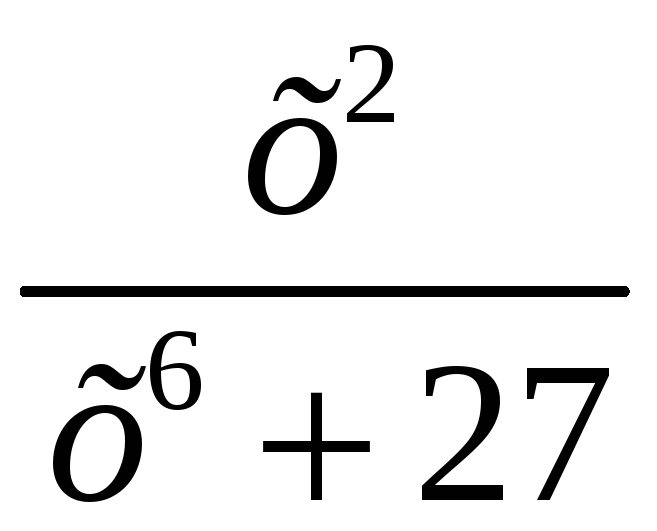 ;
;
5.
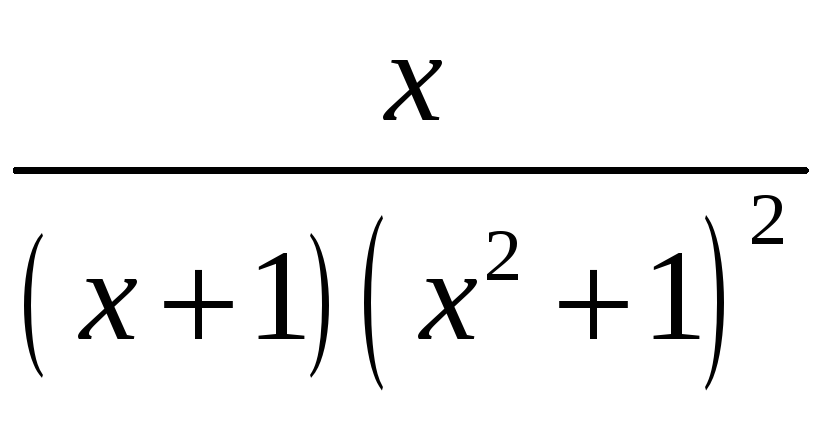 ;
6.
;
6.
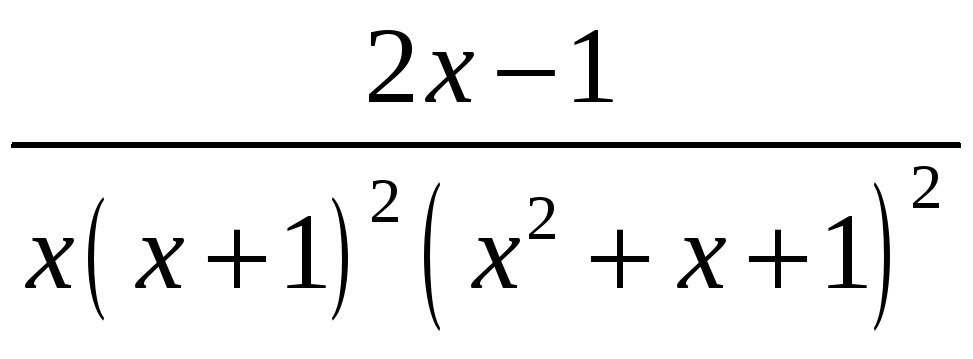 ;
;
7.
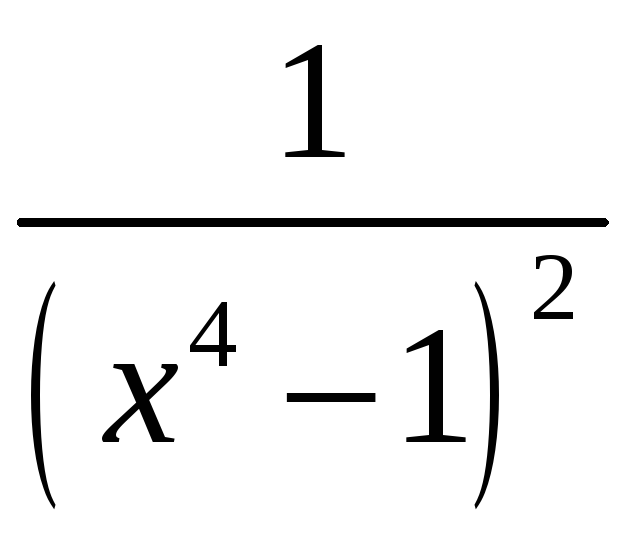
ІІ.
Розкладіть
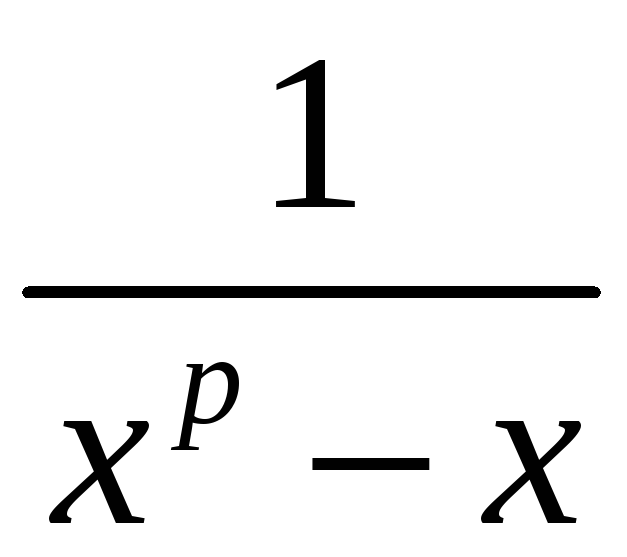 на прості дроби над полем
на прості дроби над полем
![]()
Модуль 4
Практичне заняття 5
Цілі і раціональні корені многочлена з цілими коефіцієнтами.
Критерій Ейзенштейна. Алгебраїчні і трансцендентні числа.
Будова простого алгебраїчного розширення поля
Нехай
![]() - многочлен з цілими коефіцієнтами.
- многочлен з цілими коефіцієнтами.
Якщо
нескоротній дріб
![]() є коренем многочлена
є коренем многочлена
![]() ,
то
,
то
![]() є дільником вільного члена
є дільником вільного члена
![]() ,
а
,
а
![]() - дільником старшого коефіцієнта
- дільником старшого коефіцієнта
![]() цього многочлена.
цього многочлена.
Якщо
![]() ,
то раціональні корені многочлена
,
то раціональні корені многочлена
![]() є цілими числами. Оскільки многочлени
є цілими числами. Оскільки многочлени
![]() і
і
![]() мають однакові корені, то знаходження
раціональних коренів многочлена
мають однакові корені, то знаходження
раціональних коренів многочлена
![]() можна за допомогою заміни
можна за допомогою заміни
![]() звести до відшукання цілих коренів
многочлена.
звести до відшукання цілих коренів
многочлена.
![]()
Існують
інші необхідні умови для того, щоб
раціональне число було коренем многочлена
з цілими коефіцієнтами. Зокрема, щоб
нескоротний дріб
![]() був раціональним коренем многочлена
був раціональним коренем многочлена
![]() ,
необхідно, щоб при довільному цілому
,
необхідно, щоб при довільному цілому
![]() число
число
![]() ділилося на
ділилося на
![]() де
де
![]() Така умова на практиці найчастіше
використовується для
Така умова на практиці найчастіше
використовується для
![]() ,
при цьому числа
,
при цьому числа
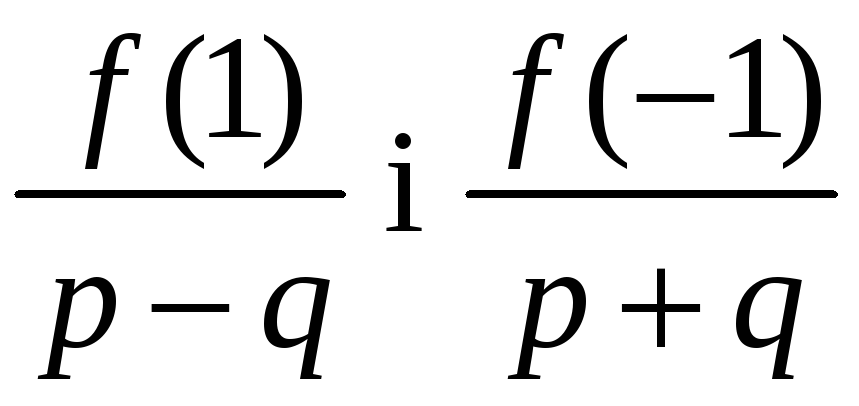 мають бути цілими.
мають бути цілими.
Многочлен
![]() з цілими коефіцієнтами є звідним у полі
з цілими коефіцієнтами є звідним у полі
![]() раціональних чисел тоді і тільки тоді,
коли існують многочлени
раціональних чисел тоді і тільки тоді,
коли існують многочлени
![]() ненульового степеня з цілими коефіцієнтами
такі, що
ненульового степеня з цілими коефіцієнтами
такі, що
![]() тобто коли многочлен
тобто коли многочлен
![]() є звідним у кільці
є звідним у кільці
![]()
Критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами.
Якщо
коефіцієнти
![]() многочлена
многочлена
![]() в кільця
в кільця
![]() діляться на деяке просте число
діляться на деяке просте число
![]() ,
причому
,
причому
![]() не ділиться на
не ділиться на
![]() а старший коефіцієнт
а старший коефіцієнт
![]() не ділиться на
не ділиться на
![]() ,
то многочлен
,
то многочлен
![]() незвідний у полі раціональних чисел.
незвідний у полі раціональних чисел.
Отже,
у кільці многочленів над полем раціональних
чисел є многочлени довільного степеня,
які незвідні у полі
![]()
Нехай
![]() - деяке числове поле. Число
- деяке числове поле. Число
![]() називають алгебраїчним
відносно поля
називають алгебраїчним
відносно поля
![]() ,
якщо воно є коренем деякого многочлена
над полем
,
якщо воно є коренем деякого многочлена
над полем
![]() .
Число, яке не є алгебраїчним відносно
поля
.
Число, яке не є алгебраїчним відносно
поля
![]() ,
називають трансцендентним
відносно
,
називають трансцендентним
відносно
![]() .
Зокрема, алгебраїчні і трансцендентні
числа і відносно поля раціональних
чисел
.
Зокрема, алгебраїчні і трансцендентні
числа і відносно поля раціональних
чисел
![]() називають відповідно просто алгебраїчним
і трансцендентними.
називають відповідно просто алгебраїчним
і трансцендентними.
Якщо
![]() є алгебраїчним числом відносно поля
є алгебраїчним числом відносно поля
![]() ,
то в кільці
,
то в кільці
![]() існує єдиний незвідний зведений многочлен
існує єдиний незвідний зведений многочлен
![]() ,
який має
,
який має
![]() своїм коренем, а його степінь
своїм коренем, а його степінь
![]() є найменшим серед степенів усіх
многочленів з коренем
є найменшим серед степенів усіх
многочленів з коренем
![]() .
При цьому многочлен
.
При цьому многочлен
![]() називають мінімальним многочленом
числа
називають мінімальним многочленом
числа
![]() ,
а його степні
,
а його степні
![]() - степенем алгебраїчного числа
- степенем алгебраїчного числа
![]() відносно поля
відносно поля
![]() .
.
Мінімальне
розширення поля
![]() ,
яке містить число
,
яке містить число
![]() називають простим розширенням поля
називають простим розширенням поля
![]() , утвореним приєднанням числа
, утвореним приєднанням числа
![]() ,
і позначають через
,
і позначають через
![]() .
Якщо
.
Якщо
![]() є алгебраїчним (трансцендентним) відносно
поля
є алгебраїчним (трансцендентним) відносно
поля
![]() ,
то
,
то
![]() називають простим
алгебраїчним (трансцендентним)
розширенням.
називають простим
алгебраїчним (трансцендентним)
розширенням.
Поле
![]() ,
утворене з поля
,
утворене з поля
![]() приєднанням кореня
приєднанням кореня
![]() незвідного у полі
незвідного у полі
![]() многочлена
многочлена
![]() -го
степеня
-го
степеня
![]()
Складається з усіх чисел виду
![]()
де
![]()
Нехай
![]() - деяке підполе поля
- деяке підполе поля
![]() .
Тоді
.
Тоді
![]() можна розглядати як векторний простір
над полем
можна розглядати як векторний простір
над полем
![]() .
При цьому розширення
.
При цьому розширення
![]() поля
поля
![]() називають скінченим, якщо
називають скінченим, якщо
![]() є скінченно-вимірним векторним простором
над
є скінченно-вимірним векторним простором
над
![]() .
При цьому розмірність простору
.
При цьому розмірність простору
![]() називають степенем розширення
називають степенем розширення
![]() над полем
над полем
![]() .
.
Просте
алгебраїчне розширення
![]() є скінченним розширенням поля
є скінченним розширенням поля
![]() ,
а степінь розширення
,
а степінь розширення
![]() над полем
над полем
![]() дорівнює степеню числа
дорівнює степеню числа
![]() відносно
відносно
![]() .
.
Розширення
![]() поля
поля
![]() ,
утворене за допомогою кількох послідовно
виконаних простих алгебраїчних розширень,
називають складеним алгебраїчним
розширенням. Розширення
,
утворене за допомогою кількох послідовно
виконаних простих алгебраїчних розширень,
називають складеним алгебраїчним
розширенням. Розширення
![]() поля
поля
![]() називають алгебраїчним, якщо всі його
елементи є алгебраїчними відносно поля
називають алгебраїчним, якщо всі його
елементи є алгебраїчними відносно поля
![]() .
.
Будь-яке
скінченне розширення поля
![]() є його алгебраїчним та складеним
розширенням . Кожне складене алгебраїчне
розширення поля
є його алгебраїчним та складеним
розширенням . Кожне складене алгебраїчне
розширення поля
![]() є простим розширенням цього поля.
є простим розширенням цього поля.
Методичні рекомендації до розв‘язування задач
Приклад 1. Розв‘язати рівняння
![]() .
.
Розв‘язання. Знайдемо спочатку раціональні корені цього рівняння (якщо вони є). Раціональними коренями тут можуть бути такі числа:
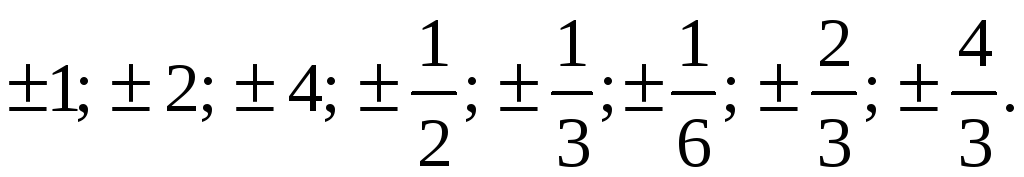 (*)
(*)
Знайдемо
межі дійсних коренів заданого рівняння.
Оскільки
![]() і
і
![]() ,
то
,
то
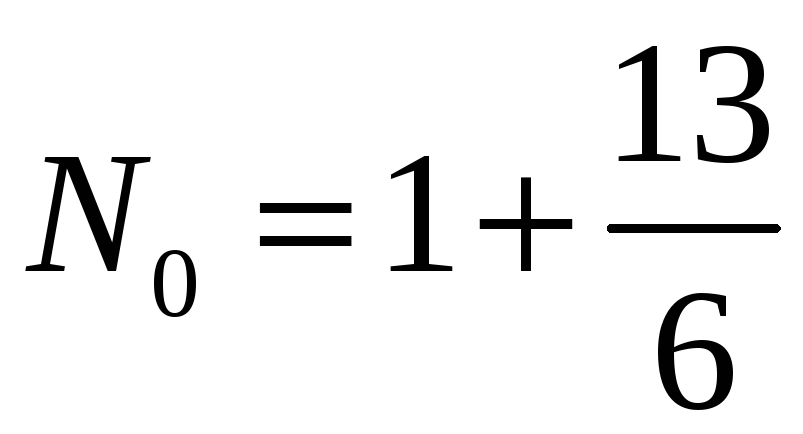 .
Отже, всі дійсні корені знаходяться в
інтервалі
.
Отже, всі дійсні корені знаходяться в
інтервалі
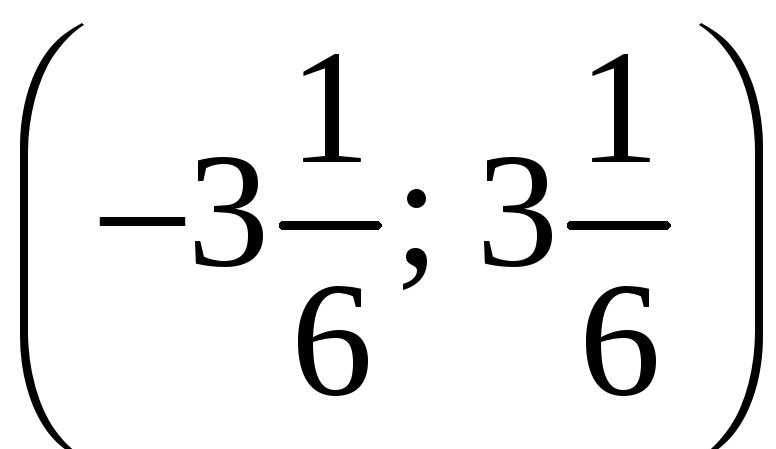 .
Серед чисел ряду (*) у цей інтервал входять
такі числа:
.
Серед чисел ряду (*) у цей інтервал входять
такі числа:
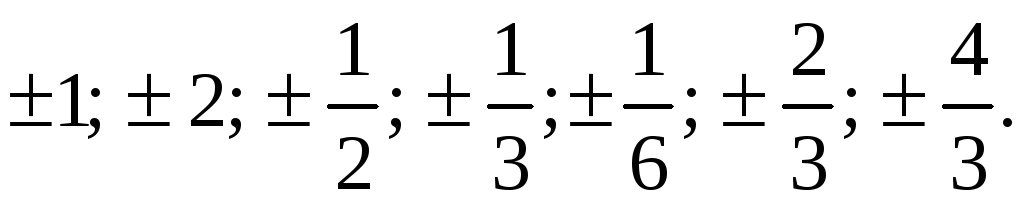 (**)
(**)
Для
заданого рівняння маємо :![]() і
і
![]() .
Поставимо умову, щоб числа
.
Поставимо умову, щоб числа
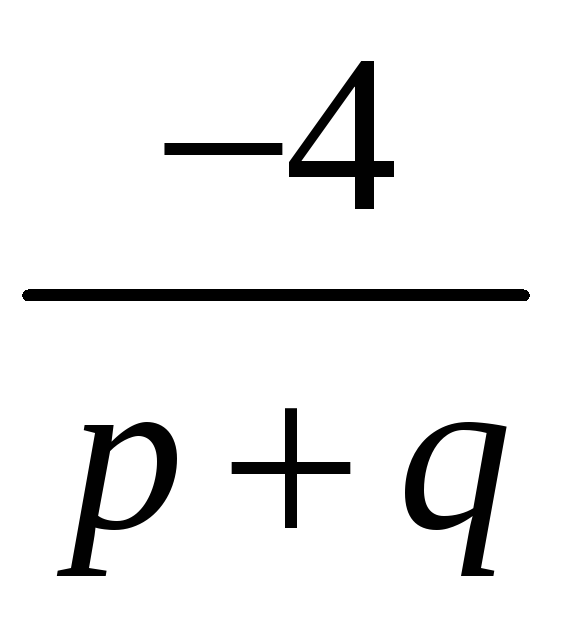 були цілими. Тоді залишаться числа:
були цілими. Тоді залишаться числа:
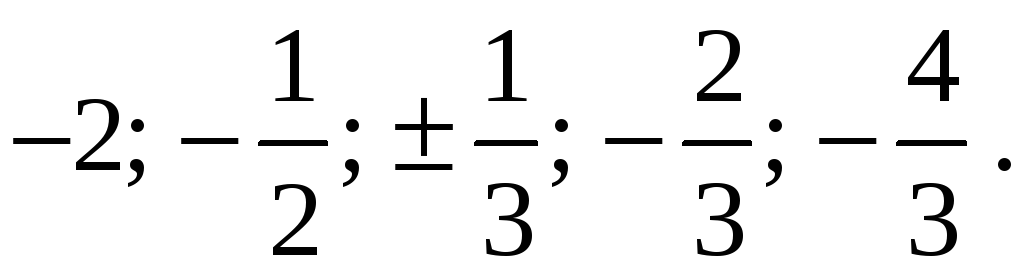 (***)
(***)
Так
як
![]() ,
то 1
є корінь рівняння.
,
то 1
є корінь рівняння.
Застосуємо схему Горнера для перевірки того, яке з чисел ряду (***) є коренем заданого рівняння.
-
6
13
3
1
– 7
– 12
– 4
1
6
19
22
23
16
4
0
– 2
6
7
8
7
2
0
2
6
19
46
99
200
–
6
4
6
4
0
–
6
1
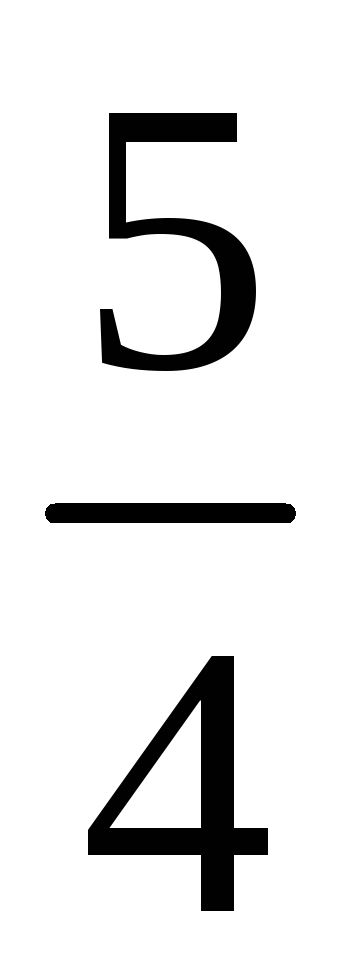
–
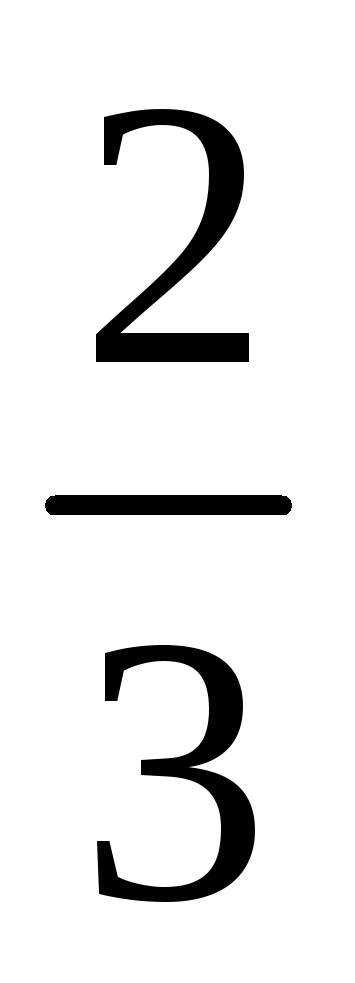
6
0
6
0
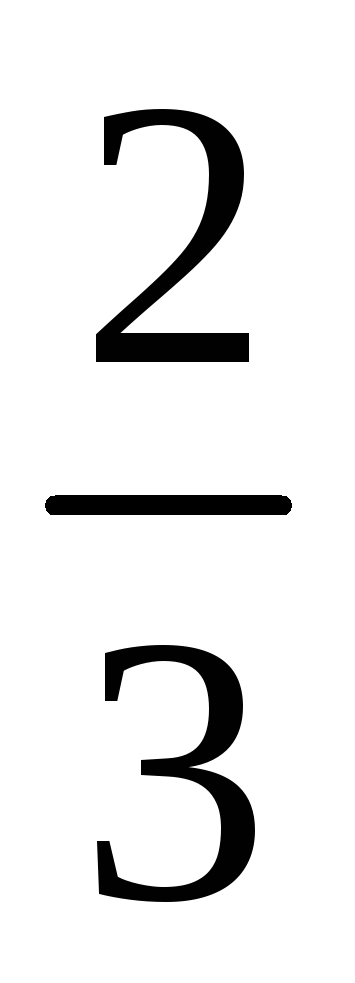
6
 4
4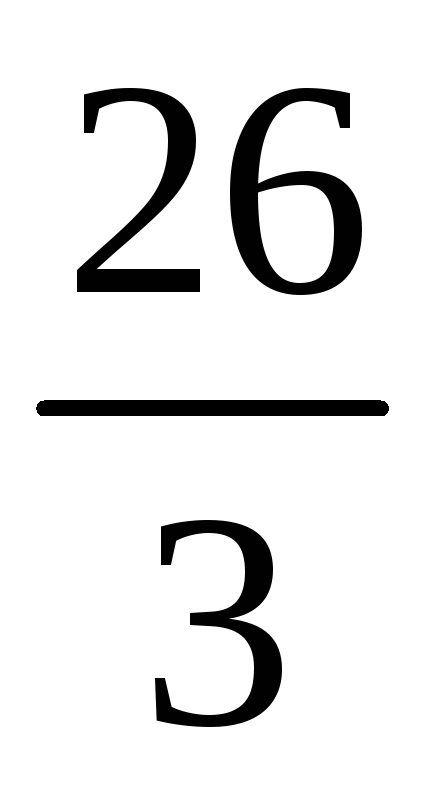
–
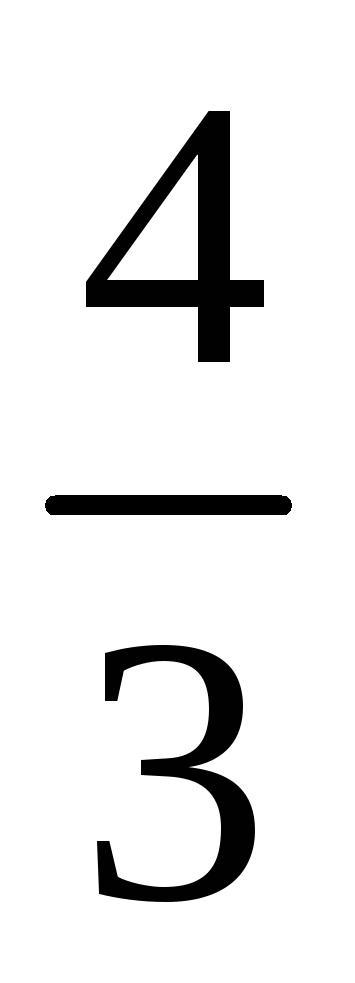
6
– 8
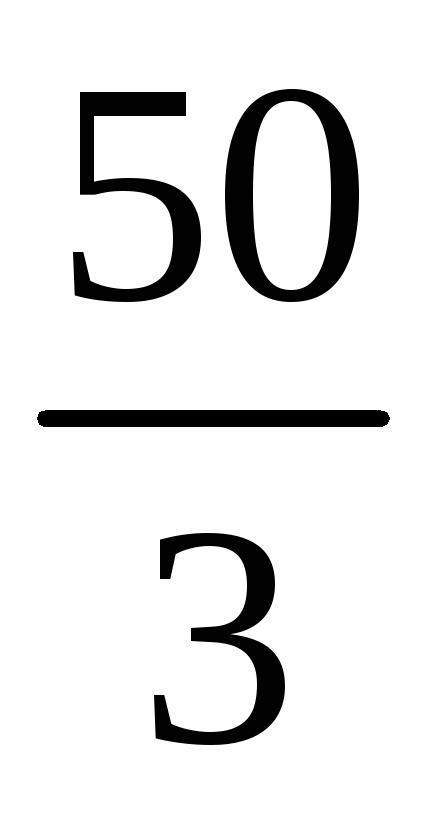
У
схемі виділено коефіцієнти повних
часток. отже, задане рівняння має чотири
раціональних корені:
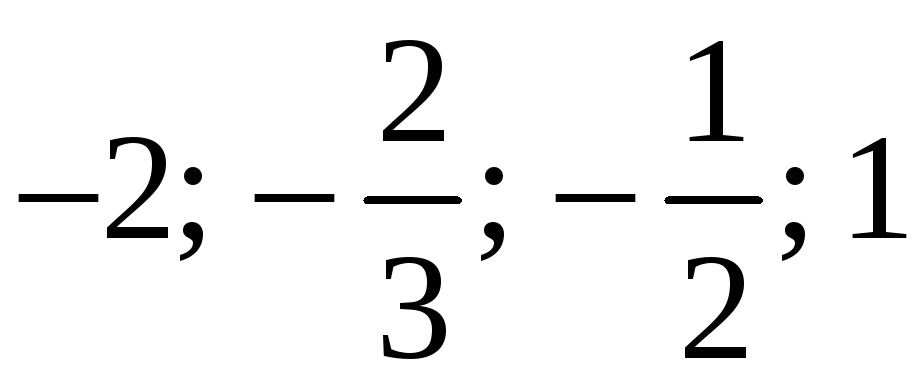 .
Решту коренів рівняння знайдемо,
прирівнюючи останню частку до нуля.
Матимемо:
.
Решту коренів рівняння знайдемо,
прирівнюючи останню частку до нуля.
Матимемо:
![]()
![]() .
.
У
цьому рівнянні комплексні корені
![]() .
Тому задане рівняння має шість різних
коренів :
.
Тому задане рівняння має шість різних
коренів :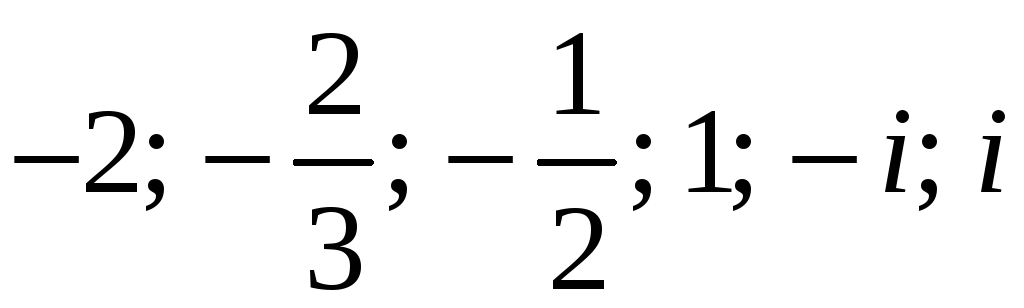 .
.