
Міністерство освіти і науки України
Миколаївський національний університет ім.. В. О. Сухомлинського
Практичні заняття з алгебри і теорії чисел
ІІ частина
Спеціальність «математика»
м. Миколаїв
2011
Білай О.В. /Під редакцією професора Будака В.Д.
Практичні заняття з алгебри і теорії чисел (частина друга)
Навчально-методичний посібник до практичних занять з алгебри і теорії чисел створено у відповідності з програмою дисципліни «Алгебра і теорії чисел» для студентів вищих навчальних закладів педагогічного профілю спеціальності «математика».
У посібнику наведено докладні зразки розв’язування прикладів і задач з алгебри і теорії чисел, пропонуються завдання для самостійного розв’язання і варіанти контрольних і індивідуальних завдань. Розглядаються методи і алгоритми розв’язування задач з наступних розділів:
·
Теорія конгруенцій. Конгруенції
![]() го
степеня. Числа і класи чисел, які належать
до даного показника. Арифметичні
застосування теорії конгруенцій.
го
степеня. Числа і класи чисел, які належать
до даного показника. Арифметичні
застосування теорії конгруенцій.
· Многочлена від однієї змінної. Подільність многочленів. Корені многочленів. Многочлени над полем раціональних чисел. Поле раціональних дробів. Розв’язування рівнянь 3-го і 4-го степеня.
Кожне практичне заняття починається з викладу теоретичних відомостей, необхідних для розв’язування задач, наводяться докладні зразки розв’язання типових задач, дається перелік задач для розв’язання в аудиторії і для домашнього завдання.
Матеріал посібника складено у відповідності з вимогами кредитно-модульної системи навчання.
Зміст
1.
Конгруенції
![]() го
степеня з
одним невідомим.
4
го
степеня з
одним невідомим.
4
2. Конгруенції другого степеня. Квадратичні лишки і нелишки 14
3. Конгруенції другого степеня за складеним модулем. Символ Якобі. 24
4. Індекси за прости модулем. Двочленні конгруенції за простим модулем. 30
5. Арифметичні застосування теорії конгруенцій. 38
6. Многочлени над полем дійсних чисел. Подільність многочленів. 41
7. Найбільший спільний дільник многочленів. Найменше спільне кратне многочленів. 53
8. Відокремлення кратних множників многочлена. 65
9. Розклад раціональних дробів на елементарні. 74
10. Цілі і раціональні корені многочлена з цілими коефіцієнтами. 79
Література. 94
Модуль 3
Практичне заняття 1
Конгруенції вищих степенів з одним невідомим.
Основні теоретичні відомості
Якщо
![]() —
попарно взаємно прості числа, то
конгруенція
—
попарно взаємно прості числа, то
конгруенція
![]() (1)
(1)
еквівалентна системі конгруенцій
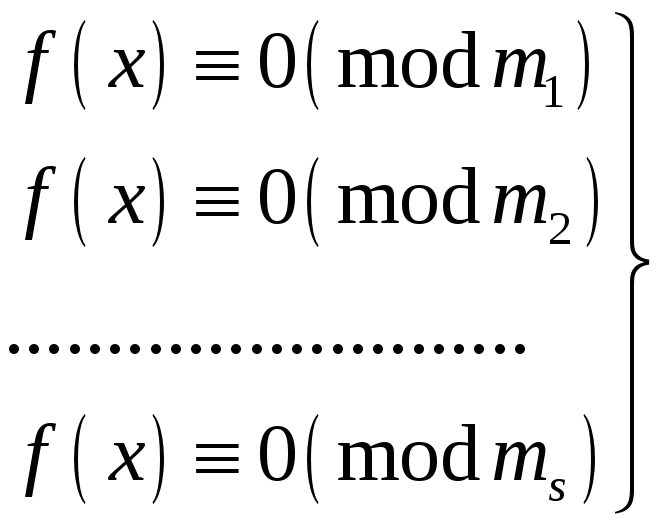 (2)
(2)
Число
розв'язків конгруенції (1) дорівнює
![]() де
де
![]() дорівнює відповідно числу розв'язків
кожної з конгруенцій (2). Отже, треба
розв'язати конгруенцію виду
дорівнює відповідно числу розв'язків
кожної з конгруенцій (2). Отже, треба
розв'язати конгруенцію виду
![]() (3)
(3)
де
![]() —
просте число,
—
просте число,
![]() .
.
Будь-який розв'язок
![]() (4)
(4)
конгруенції
![]() (5)
(5)
при
умові, що
![]() не
не
![]() ,
є одним з розв'язків конгруенції (3).
,
є одним з розв'язків конгруенції (3).
Якщо
![]() то розв'язок (4) або не дає жодного
розв'язку для (3), або дає кілька розв'язків.
то розв'язок (4) або не дає жодного
розв'язку для (3), або дає кілька розв'язків.
Нехай
![]() розв'язок
конгруенції
розв'язок
конгруенції
![]() Тоді
число
Тоді
число
![]() є розв'язком конгруенції
є розв'язком конгруенції
![]() тоді і тільки тоді, коли відповідне
значення
тоді і тільки тоді, коли відповідне
значення
![]() задовольняє
конгруенцію
задовольняє
конгруенцію
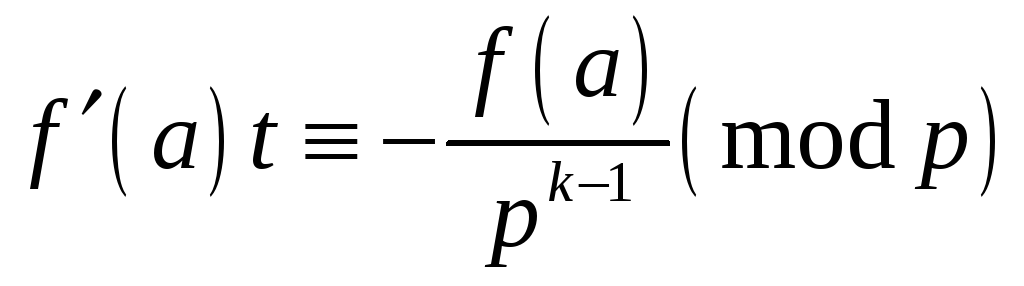 .
(6)
.
(6)
Якщо
конгруенція (6) не має розв'язків, то в
класі розв'язків
![]() конгруенції
конгруенції
![]() немає
жодного розв'язку конгруенції
немає
жодного розв'язку конгруенції
![]() .
.
Якщо
конгруенція (6) має розв'язки і
![]() , то будь-яке ціле число
, то будь-яке ціле число
![]() задовольняє конгруенцію (6), а тому
задовольняє конгруенцію (6), а тому
![]() є розв'язками (6). Тоді клас розв'язків
є розв'язками (6). Тоді клас розв'язків
![]() конгруенції
конгруенції
![]() дає
дає
![]() розв'язків конгруенції
розв'язків конгруенції
![]() ,
а саме:
,
а саме:
![]() ,
,
![]() ,
,
![]() ,
,![]()
Якщо
конгруенція (6) має розв'язки і
![]() не ділиться на
не ділиться на
![]() ,
то це
є
,
то це
є
єдиний
розв'язок
![]() .
Тоді
з класу розв'язків
.
Тоді
з класу розв'язків
![]() конгруенції
конгруенції
![]() дістаємо
єдиний розв'язок
дістаємо
єдиний розв'язок
![]() конгруенції
конгруенції
![]() .
.
Конгруенцію
(5) завжди можна замінити еквівалентною
конгруенцією того самого степеня із
старшим коефіцієнтом, що дорівнює
одиниці. Для цього слід обидві частини
конгруенції (5) помножити на число
![]() ,
яке
задовольняє конгруенцію
,
яке
задовольняє конгруенцію
![]() .
Це число визначається однозначно,
оскільки
.
Це число визначається однозначно,
оскільки
![]() .
.
Конгруенцію
(5) можна замінити еквівалентною їй
конгруенцією степеня не вище
![]() за тим самим модулем (згідно з теоремою
про пониження степеня конгруенції). Для
цього треба в конгруенції (5) замінити
вираз
за тим самим модулем (згідно з теоремою
про пониження степеня конгруенції). Для
цього треба в конгруенції (5) замінити
вираз
![]() на
на
![]() ,
де
,
де
![]() —
остача від ділення
—
остача від ділення
![]() на
на
![]() .
Ділення
.
Ділення
![]() на
на
![]() можна фактично й не виконувати, а просто
замінювати кожне
можна фактично й не виконувати, а просто
замінювати кожне
![]() у
лівій частині (5) на
у
лівій частині (5) на
![]() ,
де
,
де
![]() —
остача від ділення
—
остача від ділення
![]() на
на
![]() при умові, що остачу
при умові, що остачу
![]() замінюємо числом
замінюємо числом
![]() .
.
Якщо
![]() не
ділиться на
не
ділиться на
![]() ,
то конгруенція (5) степеня
,
то конгруенція (5) степеня
![]() має не більш ніж
має не більш ніж
![]() різних
розв'язків.
різних
розв'язків.
Конгруенція
(5) має більш як
![]() розв'язків тоді і тільки тоді, коли всі
коефіцієнти в лівій частині
розв'язків тоді і тільки тоді, коли всі
коефіцієнти в лівій частині
![]() діляться
на
діляться
на
![]() ,
тобто коли конгруенція тотожна.
,
тобто коли конгруенція тотожна.
Конгруенція
(5) степеня
![]() ,
в
якій
,
в
якій
![]() ,
,
![]() ,
має
,
має
![]() розв'язків
тоді і тільки тоді, коли всі коефіцієнти
остачі від ділення
розв'язків
тоді і тільки тоді, коли всі коефіцієнти
остачі від ділення
![]() на
на
![]() діляться
на
діляться
на
![]() .
.
Теорема
Вільсона. Натуральне
число
![]() тоді
і тільки тоді є простим, коли
тоді
і тільки тоді є простим, коли
![]() .
.
Якщо
![]() —
просте число, то конгруенція
—
просте число, то конгруенція
![]()
має
точно
![]() розв'язок.
розв'язок.
Якщо
![]() — просте число і
— просте число і
![]() —
натуральний дільник числа
—
натуральний дільник числа
![]() ,
то конгруенція
,
то конгруенція
![]()
має
точно
![]() розв'язків.
розв'язків.
Методичні рекомендації до розв‘язування задач
Приклад 1. Розв‘язати конгруенцію
![]() .
.
Розв‘язання.
Замінимо цю конгруенцію еквівалентною
їй конгруенцією степеня не вище 6 за тим
самим модулем 7. Поділимо
![]() на
на
![]() .
Дістанемо
.
Дістанемо
![]() .
.
Розв‘яжемо
конгруенцію
![]() .
Штучним способом знаходимо
.
Штучним способом знаходимо
![]() ,
,
![]() ,
,
![]() .
.
Отже,
дана конгруенція має єдиний розв‘язок
![]() .
.
Зауваження.
Замість
того, щоб ділити
![]() на
на
![]() ,
можна бу3лоб замінити
,
можна бу3лоб замінити
![]() на
на
![]() ,
де
,
де
![]() остача від ділення
остача від ділення
![]() на
на
![]() ,
причому. якщо
,
причому. якщо
![]() ділиться на
ділиться на
![]() ,
то покладемо
,
то покладемо
![]() .
.
Приклад 2. Розв‘язати конгруенцію
![]() .
.
Так
як степінь многочлена
![]() більший модуля, застосувавши вище
вказане зауваження, одержимо:
більший модуля, застосувавши вище
вказане зауваження, одержимо:
![]() ,
,
![]() ,
,
![]() .
Тоді дана конгруенція буде еквівалентна
такій:
.
Тоді дана конгруенція буде еквівалентна
такій:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Отже,
розв‘язок даної конгруенції
![]() .
.
Приклад 3. Розв‘язати конгруенцію
![]() .
.
Розв‘язання.
Випробовуючи абсолютно найменші лишки
за модулем 7, а саме:
![]() ,
знайдемо перший розв‘язок даної
конгруенції
,
знайдемо перший розв‘язок даної
конгруенції
![]() .
.
Одержуємо, за теоремою 23, дана конгруенція буде тотожна конгруенції
![]() .
.
Позначимо
![]() .
Замінимо коефіцієнти
.
Замінимо коефіцієнти
![]() на абсолютно найменші за модулем 7.
на абсолютно найменші за модулем 7.
![]() .
.
Випробуємо
далі абсолютно найменші лишки за модулем
7 стосовно многочлена
![]() .
.
![]()
![]()
![]() .
.
![]() ,
де
,
де
![]() .
.
Аналогічно
випробуємо абсолютно найменші лишки
за модулем 7 для многочлена
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Отже,
дана конгруенція має два розв‘язки, а
саме:
![]() .
.
Приклад 4. Розв‘язати конгруенцію
![]() .
.
Розв‘язання.
Оскільки
![]() ,
то задана конгруенція еквівалентна
системі конгруенцій за простими модулями:
,
то задана конгруенція еквівалентна
системі конгруенцій за простими модулями:
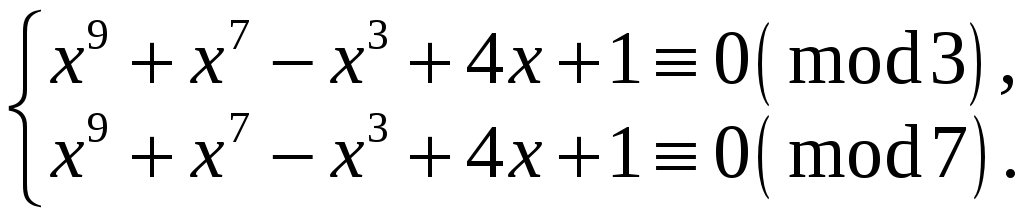
Розв‘язуємо
окремо кожну з конгруенцій.
![]() За теоремою Б,
За теоремою Б,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
![]() .
Так як
.
Так як
![]() ,
то конгруенція
,
то конгруенція
![]() має єдиний розв‘язок.
має єдиний розв‘язок.
![]() ,
,
![]() ,
,
![]() .
.
За
теоремою Б
![]() ,
,
![]() .
.
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
Розв‘язуючи
тепер спільно конгруенції
![]() і
і
![]() ,
дістанемо їхній спільний розв‘язок:
,
дістанемо їхній спільний розв‘язок:
![]() .
.
Це і буде єдиним розв‘язком цієї конгруенції.
Приклад 5. Розв‘язати конгруенцію
![]() .
.
Розв‘язання.
Оскільки
![]() ,
то задана конгруенція еквівалентна
системі
,
то задана конгруенція еквівалентна
системі
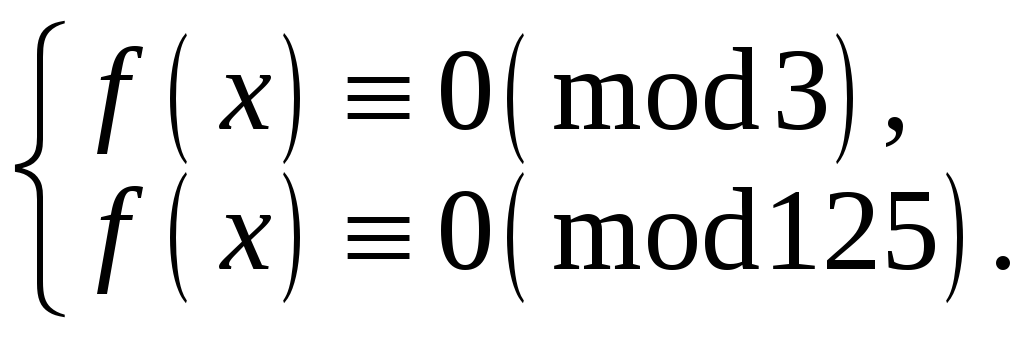
Перша з цих конгруенцій після спрощення матиме вигляд
![]() .
.
Остання
конгруенція, а отже, і конгруенція
![]() ,
матиме єдиний розв‘язок
,
матиме єдиний розв‘язок
![]() .
.
Щоб розв‘язати другу конгруенцію системи, треба спочатку розв‘язати конгруенцію
![]() ,
,
або після спрощення
![]() .
(*)
.
(*)
Методом
проб, підставляючи послідовно абсолютно
найменші лишки за модулем 5
![]() ,
знаходимо розв‘язки конгруенції (*).
,
знаходимо розв‘язки конгруенції (*).
![]() ,
,
![]() .
.
Випробуємо
![]() .
У класі
.
У класі
![]() беремо числа
беремо числа
![]() ,
де
,
де
![]() задовольняє співвідношення
задовольняє співвідношення
![]() або
або
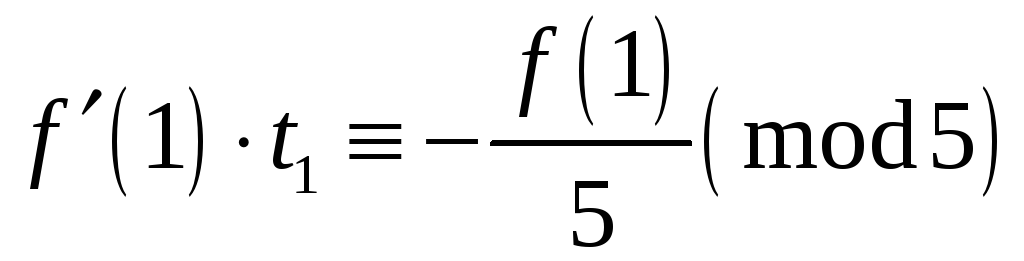 .
.
Оскільки
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() ,
тобто
,
тобто
![]() ,
або
,
або
![]() ,
,
![]() .
.
Дістаємо
![]() .
.
Знаходимо
далі
![]() ,
,
![]() і розв‘язуємо конгруенцію
і розв‘язуємо конгруенцію
![]() або
або
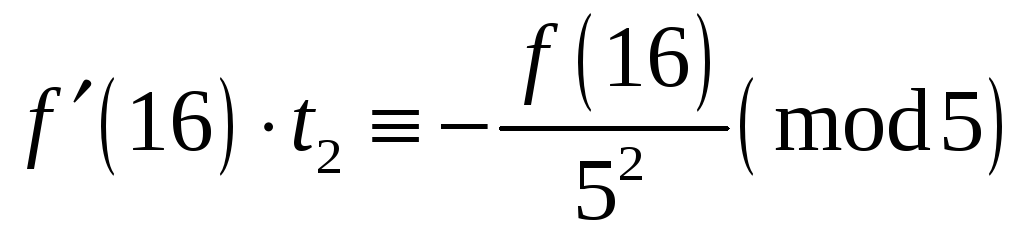 .
.
![]() ,
,
![]() ,
,
звідки
![]() ,
де
,
де
![]() .
Тоді
.
Тоді
![]() .
.
Випробуємо
клас
![]() .
У класі
.
У класі
![]() беремо числа
беремо числа
![]() ,
де
,
де
![]() задовольняє співвідношення
задовольняє співвідношення
![]() або
або
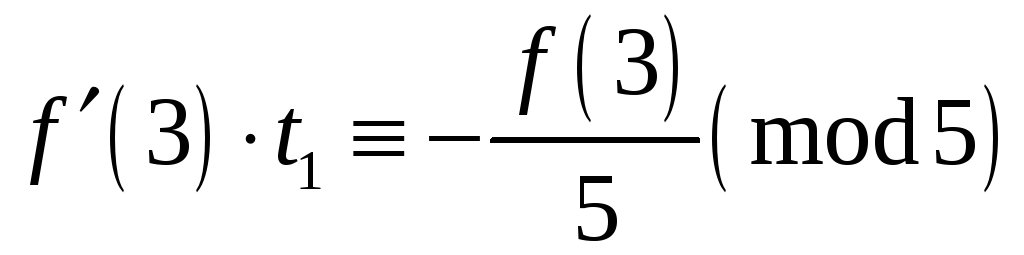 .
.
Оскільки
![]() ,
,
![]() ,
то
,
то
![]() .
Остання конгруенція не має розв‘язку,
так як
.
Остання конгруенція не має розв‘язку,
так як
![]() ,
а
,
а
![]() .
Отже, конгруенція
.
Отже, конгруенція
![]() має один розв‘язок
має один розв‘язок
![]() ,
,
![]()
Таким чином, щоб знайти розв‘язки даної конгруенції, треба розв‘язати тільки одну систему:
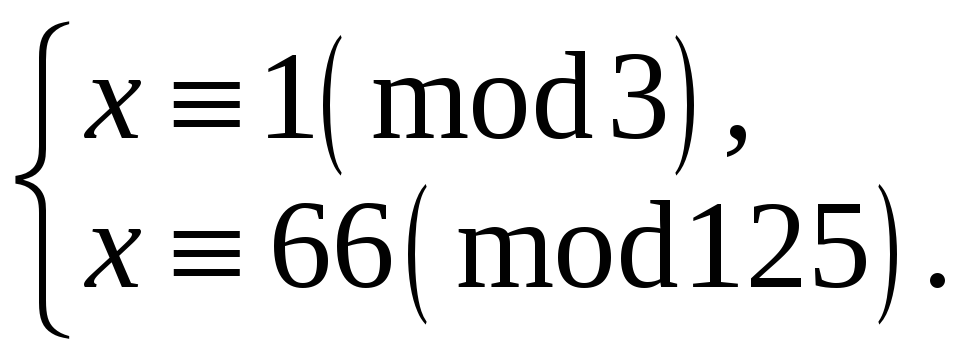
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
де
,
де
![]() .
.
![]() .
.
Відповідь:
![]() .
.
Задачі рекомендовані до розв‘язування в аудиторії
1. Звести задані конгруенції до еквівалентних їм конгруенцій, степінь яких менше за модуль, а старший коефіцієнт дорівнює 1:
а)
![]() ;
;
б)
![]() ;
;
в)
![]()
![]() ;
;
г)
![]() .
.
2. Спростити задані конгруенції (понизити степені, зменшивши коефіцієнти за абсолютною величиною, зробити так, щоб старший коефіцієнт дорівнював 1) і розв‘язати способом підбору:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
3. Спростити задані конгруенції і розв‘язати їх способом підбору:
а)
![]()
![]()
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
4. Розкласти конгруенції на лінійні множники за даним модулем:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
5. Розв‘язати конгруенції:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
Задачі рекомендовані до розв‘язування дома
1. Звести задані конгруенції до еквівалентних їм конгруенцій, степінь яких менше за модуль, а старший коефіцієнт дорівнює 1:
а)
![]()
б)
![]()
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
2. Спростити задані конгруенції (понизити степені, зменшивши коефіцієнти за абсолютною величиною, зробити так, щоб старший коефіцієнт дорівнював 1) і розв‘язати способом підбору:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
в)
![]() .
.
3. Спростити задані конгруенції і розв‘язати їх способом підбору:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
4. Розкласти конгруенції на лінійні множники за даним модулем:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
5. Розв‘язати конгруенції:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
Модуль 3
Практичне заняття 2
Конгруенції другого степеня. Зведення до двочленної конгруенції.
Квадратичні лишки і нелишки. Символ Лежандра
Основні теоретичні відомості
Конгруенцію другого степеня виду
![]() ,
,
![]() (1)
(1)
завжди можна звести до двочленної конгруенції виду
![]() (2)
(2)
де
![]() ,
,
![]() ,
,
![]() .
.
Для
цього слід обидві частини і модуль
конгруенції (1) помножити на
![]() і
зробити відповідні перетворення.
і
зробити відповідні перетворення.
Якщо
конгруенція (2) має хоча б один розв'язок,
то
![]() називається
квадратичним
лишком за модулем
називається
квадратичним
лишком за модулем
![]() , у
противному разі
, у
противному разі
![]() називається квадратичним
нелишком за модулем
називається квадратичним
нелишком за модулем
![]() .
При
цьому
.
При
цьому
![]() .
.
Розв'язування конгруенції виду (2) за складеним модулем зводиться до розв'язування таких конгруенцій:
1)
![]() ,
де
,
де
![]() —
непарне просте число;
(3)
—
непарне просте число;
(3)
2)
![]() ,
де
,
де
![]() —
непарне просте число,
—
непарне просте число,![]() ;
(4)
;
(4)
3)
![]() ,
де
,
де
![]() .
(5)
.
(5)
Найбільш
важливим є той випадок, коли модуль є
непарним простим числом. При цьому
досить обмежитися випадком, коли
![]() ,
оскільки в противному разі конгруенція
(3) має єдиний розв'язок
,
оскільки в противному разі конгруенція
(3) має єдиний розв'язок
![]() .
.
Отже, надалі розглядатимемо таку конгруенцію:
![]() ,
,
![]() ,
де
,
де
![]() — просте
непарне число.
(6)
— просте
непарне число.
(6)
Якщо
![]() — квадратичний лишок за модулем
— квадратичний лишок за модулем
![]() ,
то
конгруенція (6) має два розв'язки.
,
то
конгруенція (6) має два розв'язки.
Для
будь-якого простого непарного числа
![]() половина
лишків зведеної системи лишків є
квадратичними лишками, а половина —
квадратичними нелишками.
половина
лишків зведеної системи лишків є
квадратичними лишками, а половина —
квадратичними нелишками.
При
простому непарному
![]() число
число
![]() є
квадратичним лишком за модулем
є
квадратичним лишком за модулем
![]() тоді
і тільки тоді, коли
тоді
і тільки тоді, коли
![]() ,
і
квадратичним нелишком тоді і тільки
тоді, коли
,
і
квадратичним нелишком тоді і тільки
тоді, коли
![]() (критерій
Ейлера).
(критерій
Ейлера).
Теорема
Ейлера.
Добуток
двох квадратичних лишків або нелишків
є квадратичним лишком за модулем
![]() ;
добуток квадратичного лишку на нелишок
є квадратичним нелишком.
;
добуток квадратичного лишку на нелишок
є квадратичним нелишком.
Добуток
ряду чисел
![]() дає квадратичний лишок або нелишок
залежно від того, парне чи непарне число
нелишків буде серед множників.
дає квадратичний лишок або нелишок
залежно від того, парне чи непарне число
нелишків буде серед множників.
Для
ефективного використання критерію
Ейлера вводиться так званий символ
Лежандра
![]() (читається: «символ Лежандра
(читається: «символ Лежандра
![]() відносно
відносно
![]() »,
або
коротше «
»,
або
коротше «![]() відносно
відносно
![]() »,
або «
»,
або «![]() до
до
![]() »),
»),
![]() називається
чисельником, а
називається
чисельником, а
![]() — знаменником символу Лежандра.
— знаменником символу Лежандра.
Символ
Лежандра
![]() визначається для всіх цілих чисел
визначається для всіх цілих чисел
![]() ,
які
не діляться на просте непарне число
,
які
не діляться на просте непарне число
![]() ,
рівністю
,
рівністю

Критерій Ейлера тоді коротко записується так:
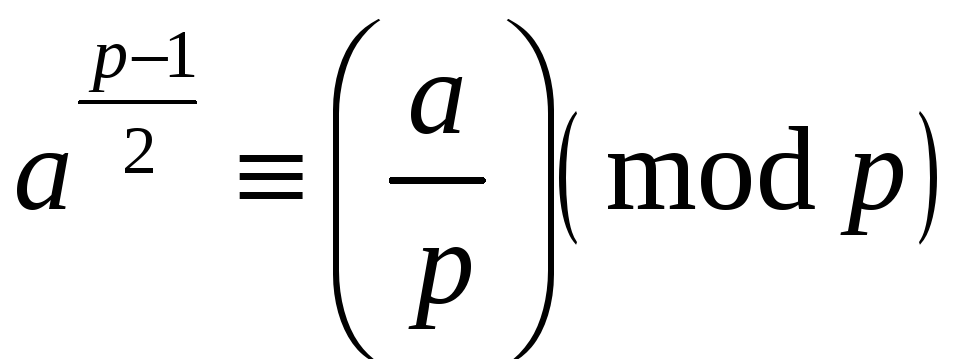 .
.
Основні властивості символу Лежандра:
1°.Якщо
![]() ,
то
,
то
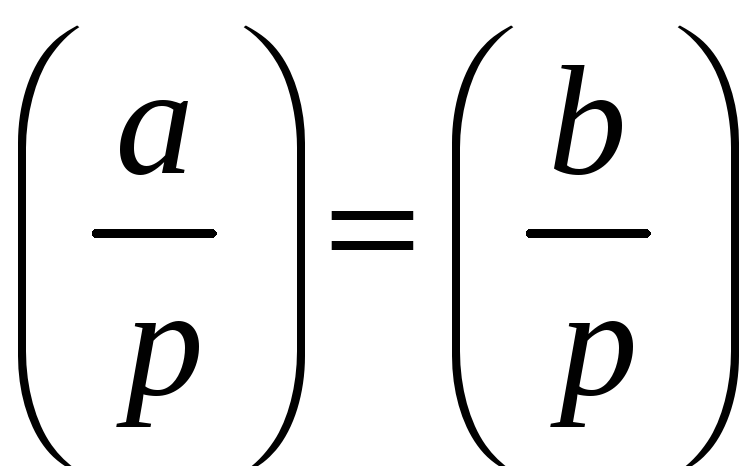 ;
;
2º.
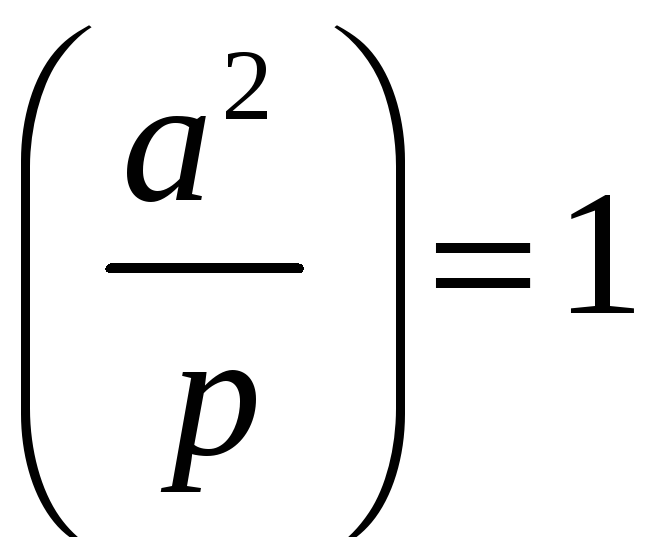 ;
;
3º.
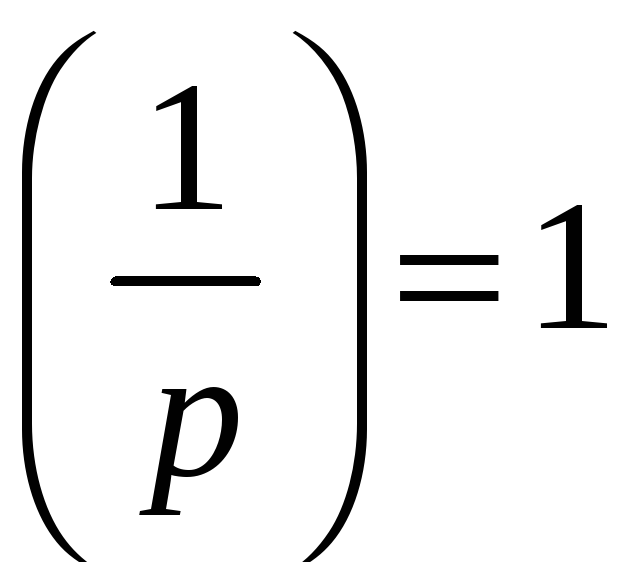 ;
;
4º.
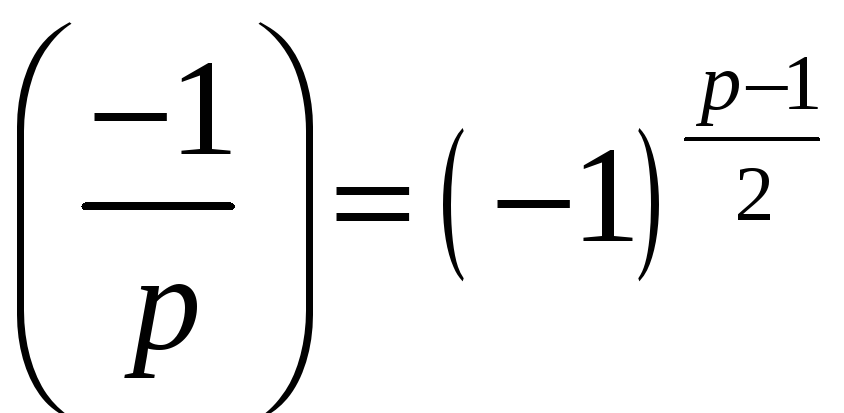 ;
;
5º.
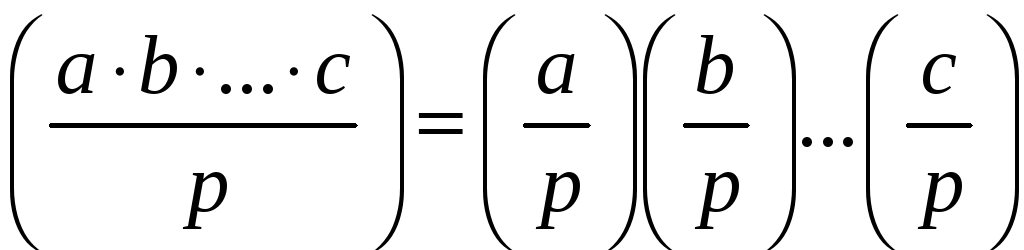 ;
;
6º.
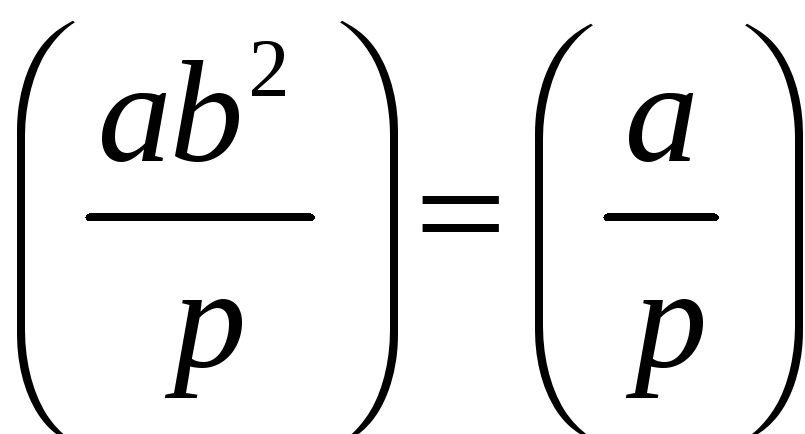 ;
;
7º
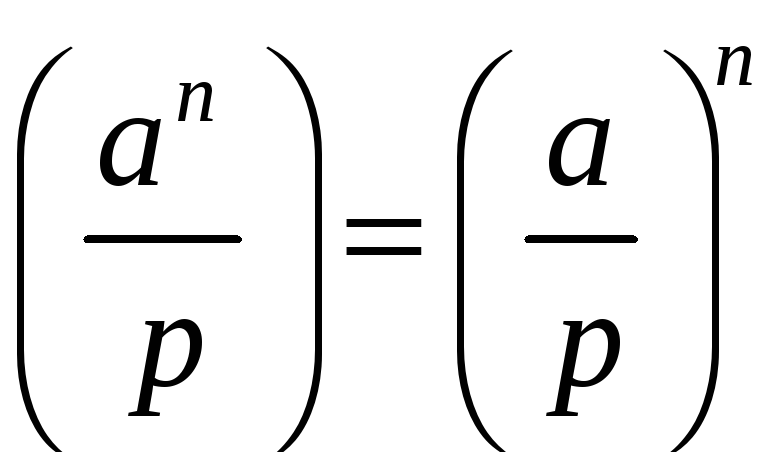 ;
;
8º
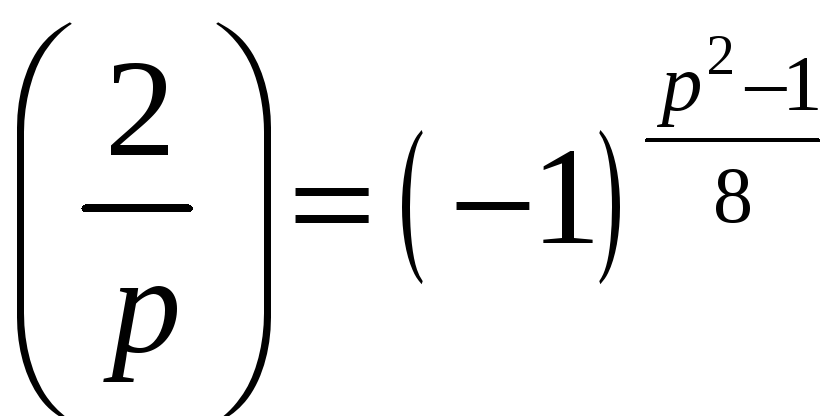 ;
;
9°.
Якщо
![]() і
і
![]() —
різні непарні прості числа, то
—
різні непарні прості числа, то

(закон взаємності квадратичних лишків).
Узагальненням
символу Лежандра є символ
Якобі
![]() (читається: «символ Якобі
(читається: «символ Якобі
![]() відносно
відносно
![]() »).
Він визначається для будь-яких непарних
натуральних чисел
»).
Він визначається для будь-яких непарних
натуральних чисел
![]() і чисел
і чисел
![]() ,
взаємно
простих з
,
взаємно
простих з
![]() ,
рівністю
,
рівністю
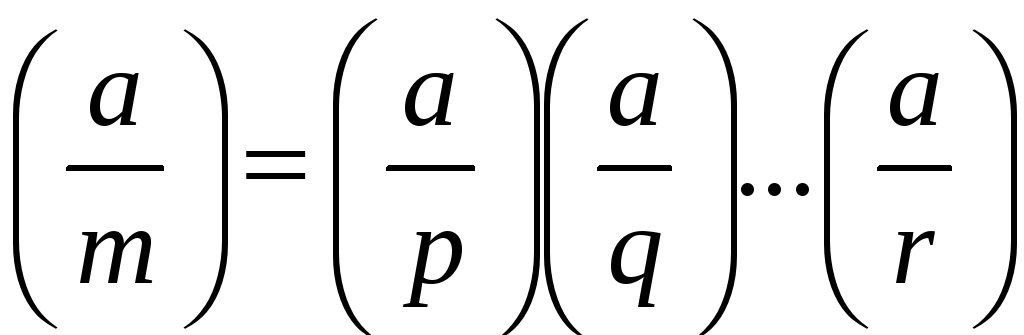 ,
,
де
![]() є розкладом
є розкладом
![]() на прості множники (серед них можуть
бути і рівні), тобто як добуток символів
Лежандра. Для символу Якобі зберігаються
властивості 1) — 9) символу Лежандра,
проте для символу Якобі йдеться не про
непарні прості числа
на прості множники (серед них можуть
бути і рівні), тобто як добуток символів
Лежандра. Для символу Якобі зберігаються
властивості 1) — 9) символу Лежандра,
проте для символу Якобі йдеться не про
непарні прості числа
![]() ,
а
про непарні натуральні числа
,
а
про непарні натуральні числа
![]() ,
для властивості 9) — про взаємно прості
непарні числа, відмінні від 1. Тому при
визначенні символу Лежандра зручно
розглядати його як символ Якобі. При
цьому часто немає потреби виділяти з
чисельника символу його непарні прості
множники.
,
для властивості 9) — про взаємно прості
непарні числа, відмінні від 1. Тому при
визначенні символу Лежандра зручно
розглядати його як символ Якобі. При
цьому часто немає потреби виділяти з
чисельника символу його непарні прості
множники.
Конгруенція
![]() ,
де
,
де
![]() — непарне
просте число,
— непарне
просте число,
![]() ,
,
![]() ,
має два розв'язки, якщо
,
має два розв'язки, якщо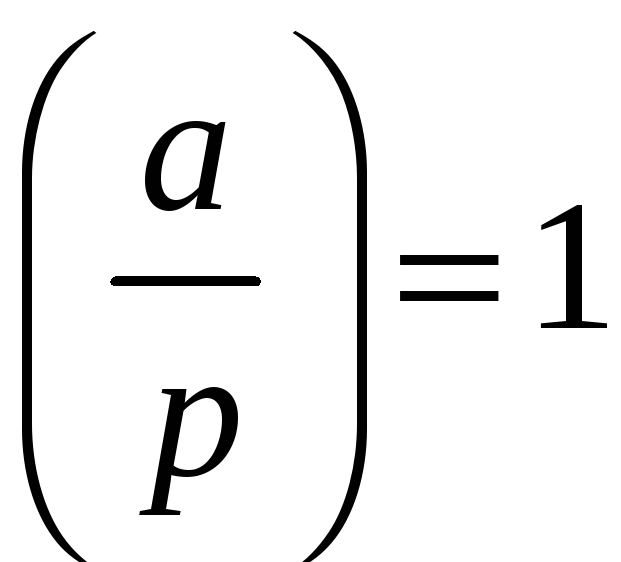 ,
і не має їх зовсім, якщо
,
і не має їх зовсім, якщо
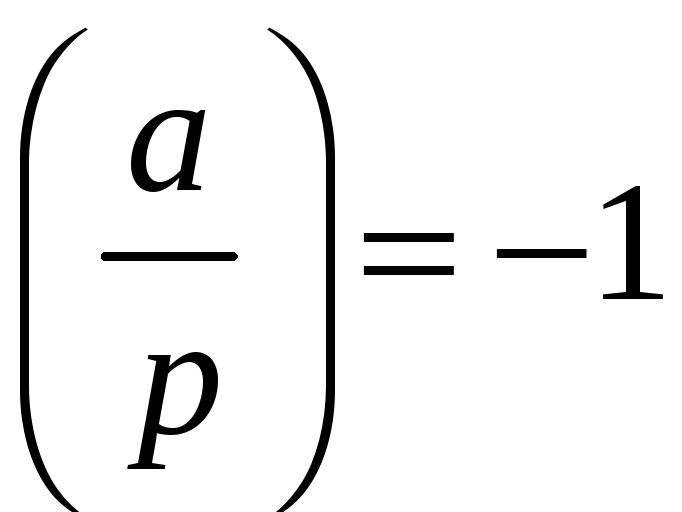 .
.
Для
конгруенції
![]() ,
,
![]() ,
необхідними умовами існування розв'язків
є
,
необхідними умовами існування розв'язків
є
![]() при
при
![]() ,
,
![]() при
при
![]() .
.
Якщо
ці умови виконуються, то існує один
розв'язок при
![]() ;
два розв'язки при
;
два розв'язки при
![]() і чотири розв'язки при
і чотири розв'язки при![]() .
.
Для
конгруенції загального виду
![]() ,
,
![]() ,
,
![]() ,
необхідними і достатніми умовами
існування розв'язків є:
,
необхідними і достатніми умовами
існування розв'язків є:
![]() при
при
![]() ;
;
![]() при
при
![]() .
.
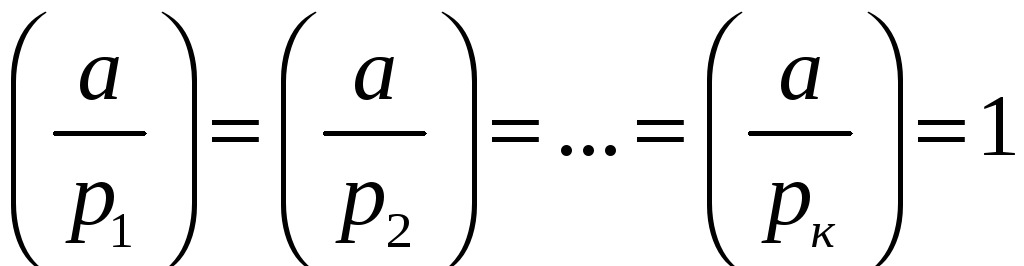 .
.
Якщо жодну з цих умов не порушено, то число розв'язків дорівнюватиме:
![]() при
при
![]() і
і
![]() ;
;
![]() при
при
![]() ;
;
![]() при
при
![]() .
.
Методичні рекомендації до розв‘язування задач
Приклад
1.
Скільки розв‘язків має конгруенція
![]() ?
?
Розв‘язання.
За властивостями конгруенцій
![]()
![]() .
Знайдемо символ Лежандра
.
Знайдемо символ Лежандра
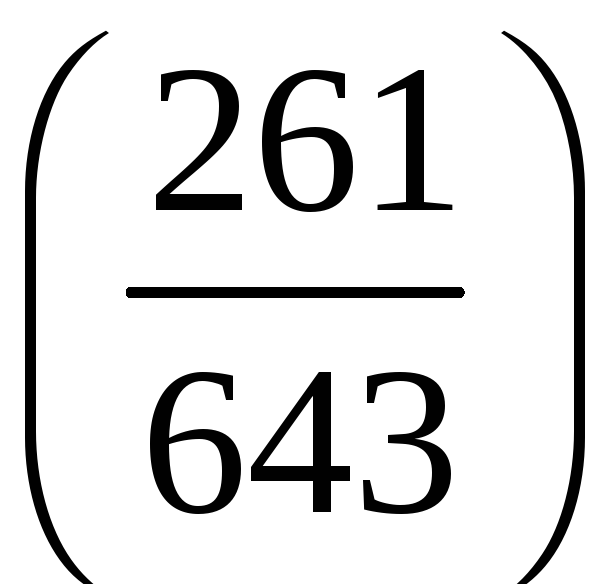 .
Оскільки
.
Оскільки
![]() ,
а
,
а
![]() – просте число, то, згідно з властивістю
6,
– просте число, то, згідно з властивістю
6,
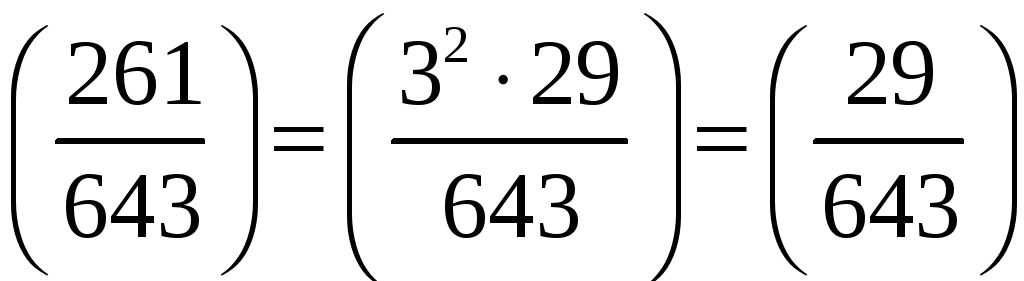 .
.
Обчислимо
символ Лежандра
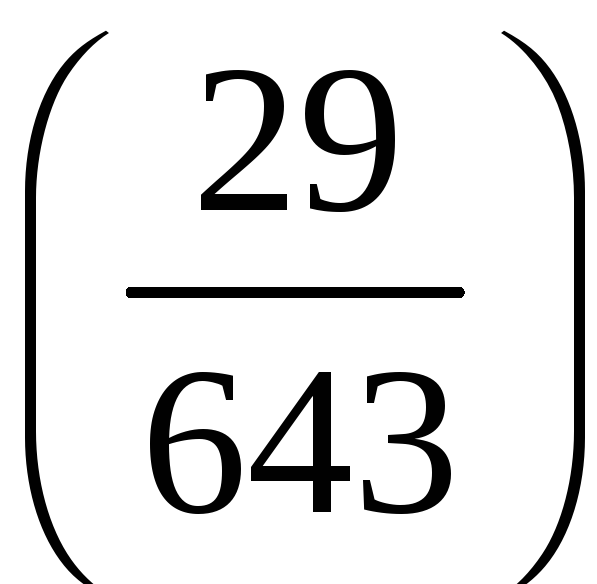 .
Оскільки 29 і 643 – різні прості непарні
числа, то внаслідок закону взаємності
9) дістаємо
.
Оскільки 29 і 643 – різні прості непарні
числа, то внаслідок закону взаємності
9) дістаємо
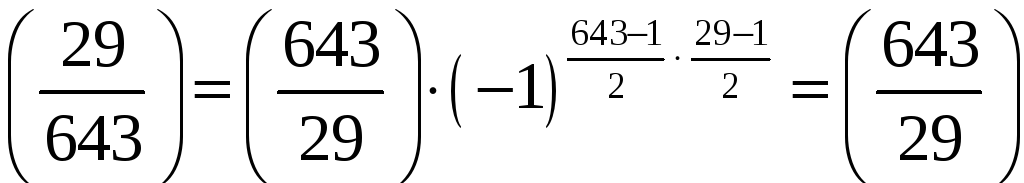 .
.
За властивістю 1) маємо
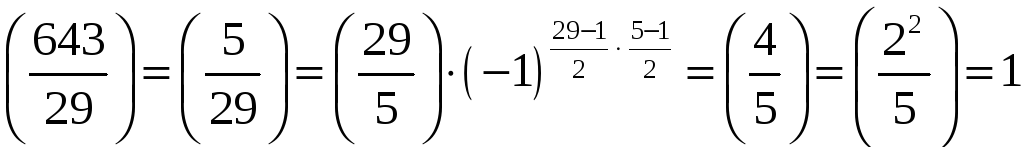 .
.
Отже, дана конгруенція має два розв‘язки.
Зауваження.
1.
Слід уважно застосовувати властивість
9), оскільки якщо хоч одне з чисел
![]() чи
чи
![]() є складеним, застосування цієї властивості
може призвести до помилок в обчисленні
символу Лежандра.
є складеним, застосування цієї властивості
може призвести до помилок в обчисленні
символу Лежандра.
2.
Зауважимо, що коли
![]() – просте непарне число, то символ
Лежандра
– просте непарне число, то символ
Лежандра
![]() є для конгруенції
є для конгруенції
![]() символом Якобі
символом Якобі
![]() і навпаки. Тому для конгруенцій за
простим модулем можна не розрізняти
символів Лежандра і Якобі, що дає змогу
при обчисленні символів Лежандра не
розкладати чисельник на прості множники.
треба тільки виділяти множники, що
дорівнюють
і навпаки. Тому для конгруенцій за
простим модулем можна не розрізняти
символів Лежандра і Якобі, що дає змогу
при обчисленні символів Лежандра не
розкладати чисельник на прості множники.
треба тільки виділяти множники, що
дорівнюють
![]() .
Якщо
.
Якщо
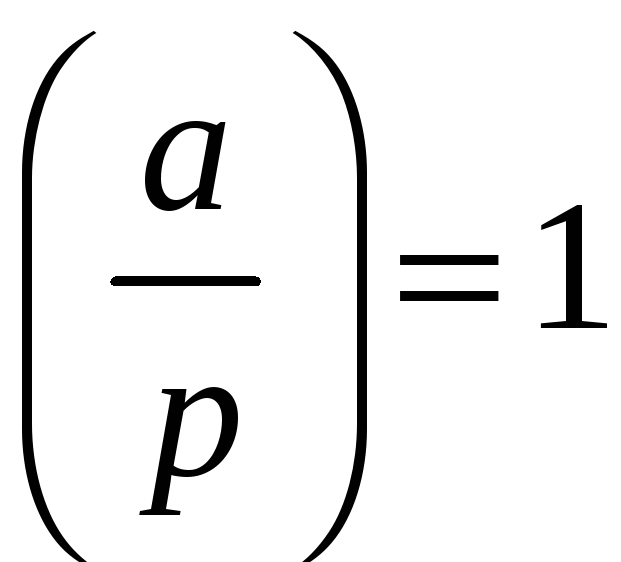 ,
то ця конгруенція має два розв‘язки;
якщо
,
то ця конгруенція має два розв‘язки;
якщо
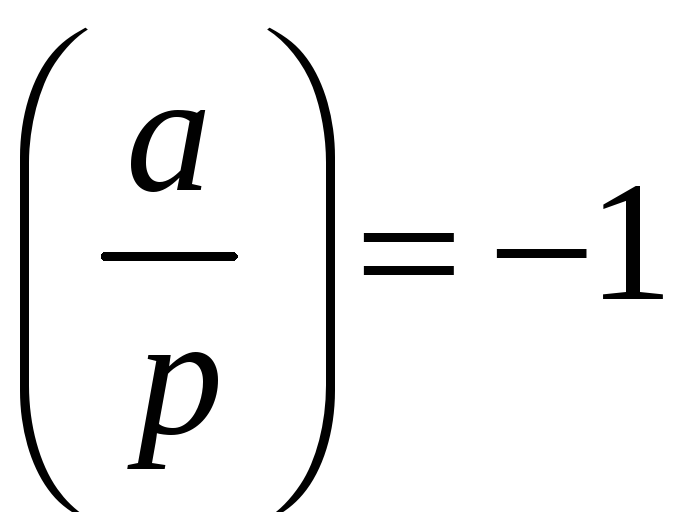 ,
то конгруенція розв‘язків не має. Для
конгруенції
,
то конгруенція розв‘язків не має. Для
конгруенції
![]() ,
де
,
де
![]() непарне
складене число, символ Лежандра не
існує, а символ Якобі існує. Проте, якщо
символ Якобі
непарне
складене число, символ Лежандра не
існує, а символ Якобі існує. Проте, якщо
символ Якобі
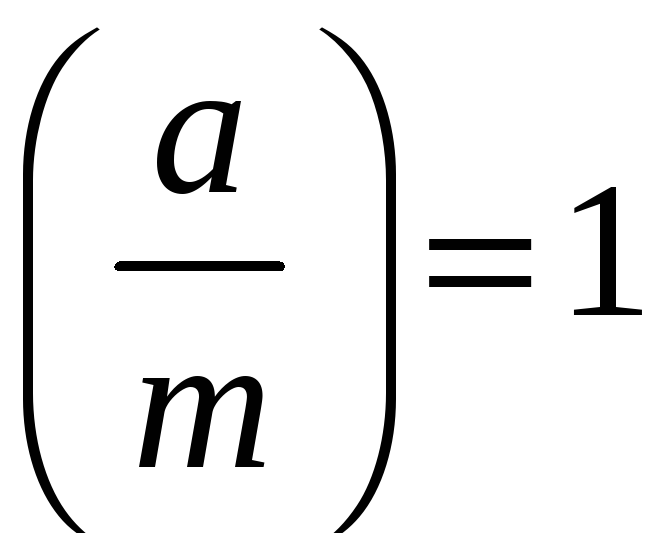 і
і
![]() непарне
складене число, то це ще не означає, що
конгруенція
непарне
складене число, то це ще не означає, що
конгруенція
![]() має розв‘язки. Так конгруенція
має розв‘язки. Так конгруенція
![]() розв‘язків не має, а символ Якобі для
неї
розв‘язків не має, а символ Якобі для
неї
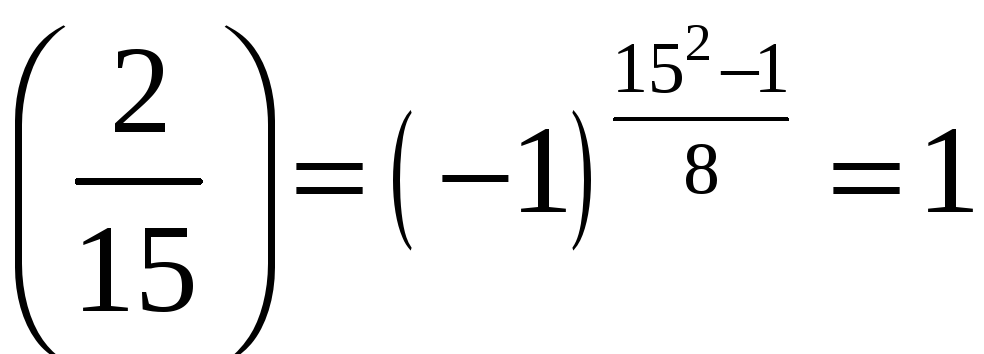 .
.
Приклад
2.
Розв‘язати способом проб конгруенцію
![]() .
.
Розв‘язання.
Спочатку знаходимо
![]() .
Числа 3
і 7
непарні прості. Обчислимо символ Лежандра
.
Числа 3
і 7
непарні прості. Обчислимо символ Лежандра
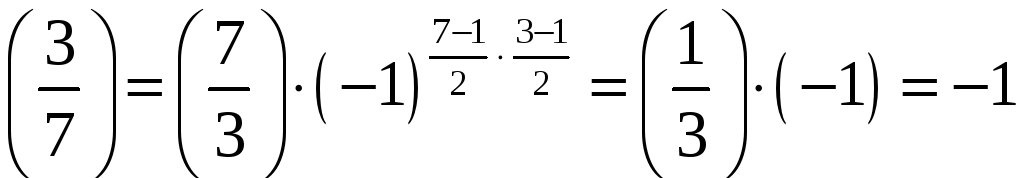 .
.
Отже, дана конгруенція не має розв‘язків.
Приклад
3.
Розв‘язати конгруенцію
![]() .
.
Розв‘язання.
Для простого модуля старший коефіцієнт
взаємно простий з ним. Тоді процес
зведення заданої конгруенції до
двочленної можна скоротити і навіть
залишити модуль незмінним. Так як
![]() ,
то модуль конгруенції можна не множити
на
,
то модуль конгруенції можна не множити
на
![]() .
Помножаючи обидві частини конгруенції
на 20 за модулем 43, дістаємо
.
Помножаючи обидві частини конгруенції
на 20 за модулем 43, дістаємо
![]() ,
,
або
![]() ,
,
![]() .
.
Позначимо
![]() і тоді буде
і тоді буде
![]() .
Остання конгруенція має два розв‘язки:
.
Остання конгруенція має два розв‘язки:
![]() ,
,
![]() .
.
Отже,
квадратна конгруенція
![]() має
розв‘язки тоді, коли мають розв‘язки
конгруенції:
має
розв‘язки тоді, коли мають розв‘язки
конгруенції:
![]() і
і
![]() .
Розв‘язуючи дві останні конгруенції,
матимемо:
.
Розв‘язуючи дві останні конгруенції,
матимемо:
![]() і
і
![]() .
.
Тоді
задана конгруенція має розв‘язки
![]() .
.
Приклад
4.
Розв‘язати конгруенцію
![]() .
.
Розв‘язання.
Конгруенцію
![]() замінюємо системою за простими модулями
замінюємо системою за простими модулями
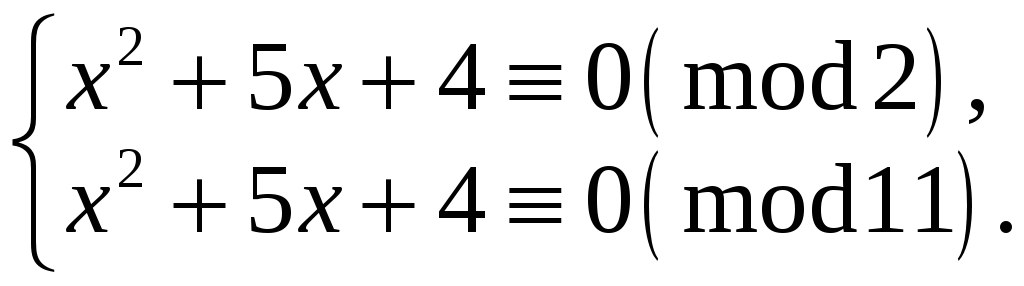
Спочатку
розв‘язуємо конгруенцію
![]() .
Застосуємо елементарні перетворення
над конгруенціями до виразу зліва
.
Застосуємо елементарні перетворення
над конгруенціями до виразу зліва
![]() .
Конгруенція
.
Конгруенція
![]() має розв‘язки
має розв‘язки
![]() .
.
Далі
розв‘язуємо конгруенцію
![]() .
Помножаючи обидві частини конгруенції
на 4 за модулем 11, дістаємо
.
Помножаючи обидві частини конгруенції
на 4 за модулем 11, дістаємо
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
Тепер складаємо системи конгруенцій за модулями 2 і 11.
а) б)
б)
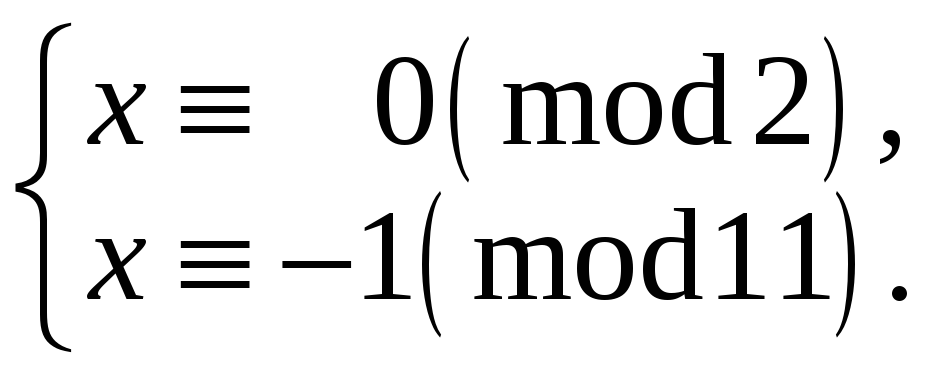
в)
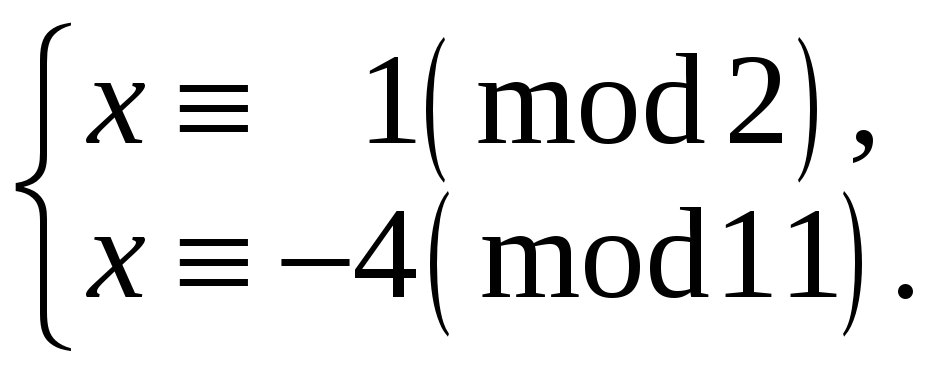 г)
г)
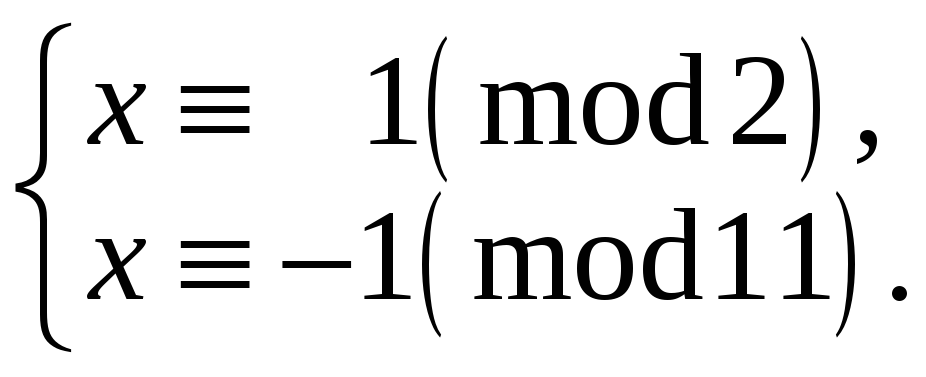
Розв‘яжемо
систему а):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Отже,
.
Отже,
![]()
![]() .
.
Система
конгруенцій б) має розв‘язок:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Отже,
.
Отже,
![]() .
.
Розмірковуючи
аналогічно, знаходимо розв‘язки систем
в)
![]() ,
,
![]() і г)
і г)
![]() ,
,
![]() .
.
Відповідь:
![]() .
.
Приклад
5.
Розв‘язати в цілих числах рівняння
![]() .
.
Розв‘язання. Перетворимо дане рівняння і зведемо його до конгруенції.
![]() ,
,
![]() .
Помножимо обидві частини конгруенції
на
.
Помножимо обидві частини конгруенції
на
![]() .
.
![]() .
.
![]() .
Виконаємо підстановку
.
Виконаємо підстановку
![]() ,
матимемо:
,
матимемо:
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]()
![]()
![]()
![]() .
.
Знайдемо
![]() ,
яке відповідатиме
,
яке відповідатиме
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]()
![]()
![]()
![]() .
.
Знайдемо
![]() ,
яке відповідатиме
,
яке відповідатиме
![]() ,
,
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Відповідь:
![]() ,
,
![]() ;
;
![]()
![]() ,
,
![]() .
.
Задачі рекомендовані для розв‘язування в аудиторії
1. Знайти значення символу Лежандра:
а)
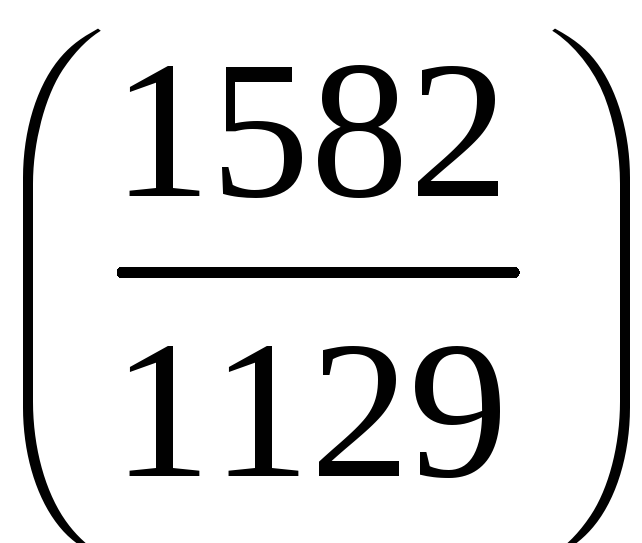 ;
б)
;
б)
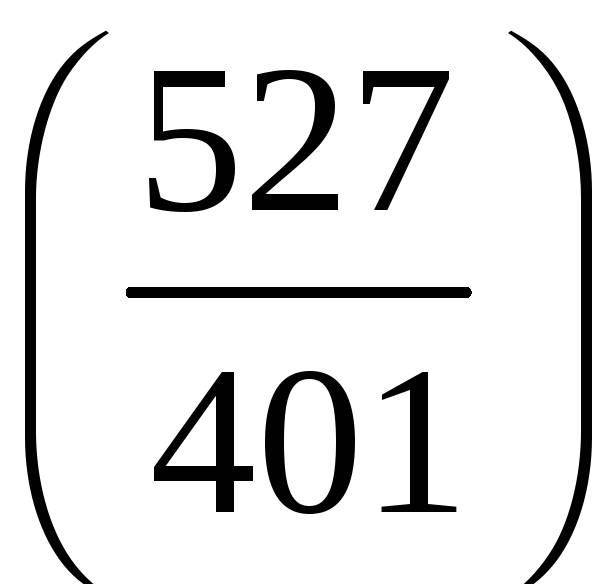 ;
в)
;
в)
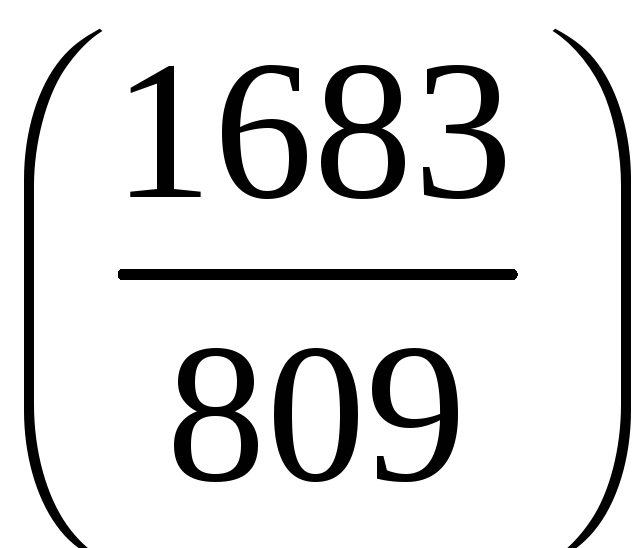 ;
г)
;
г)
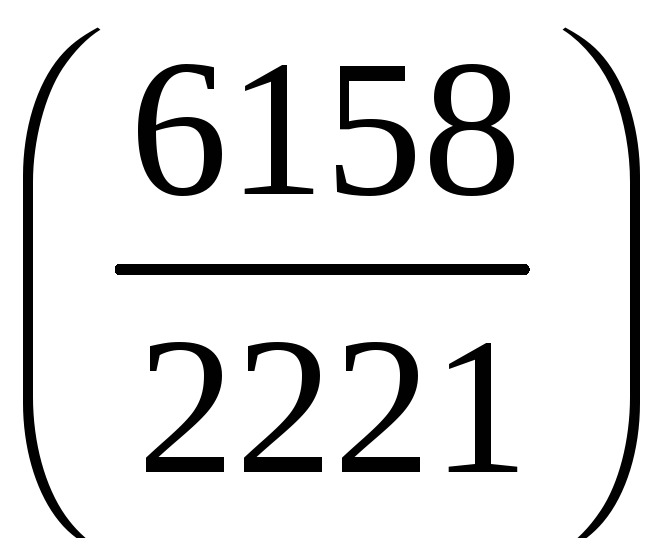 ;
д)
;
д)
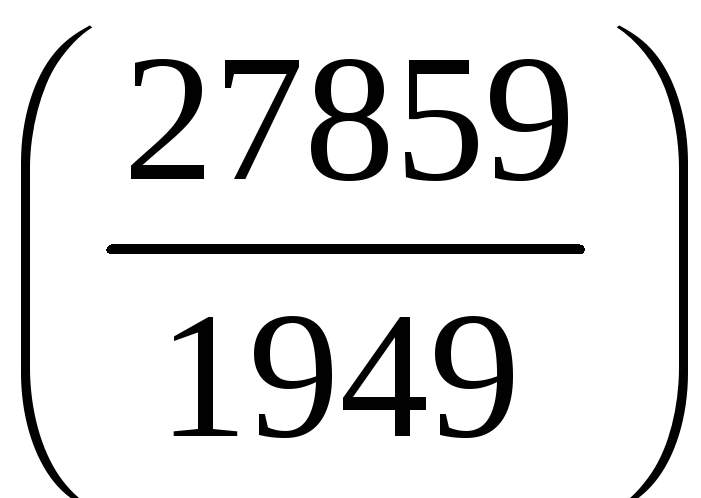 ;
;
е)
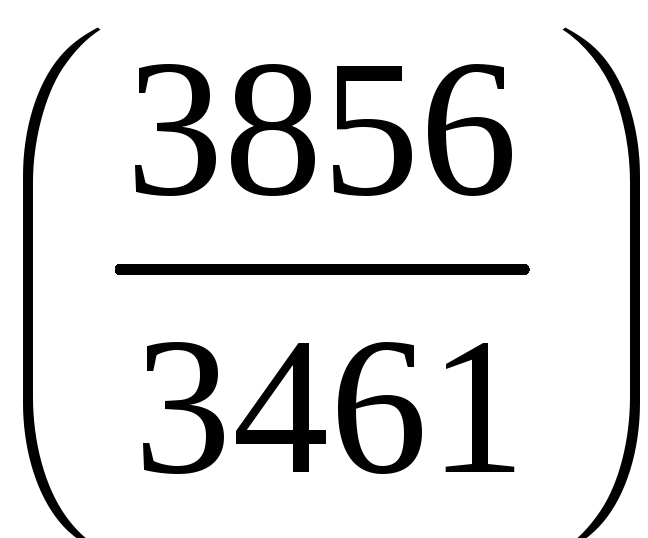 ;
є)
;
є)
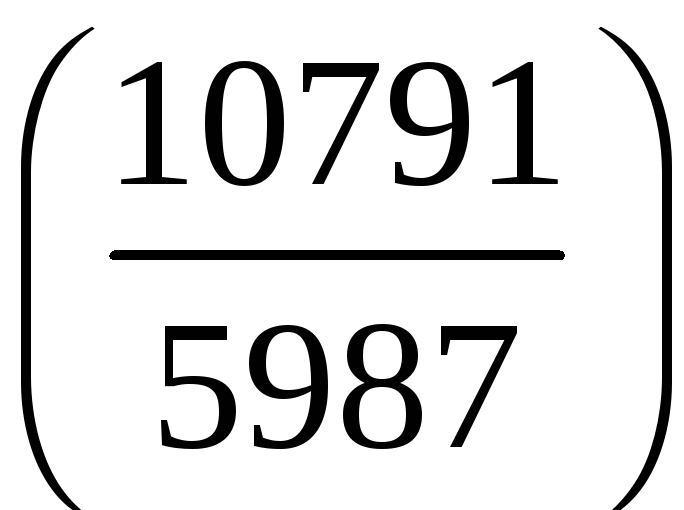 ;
ж)
;
ж)
 ;
з)
;
з)
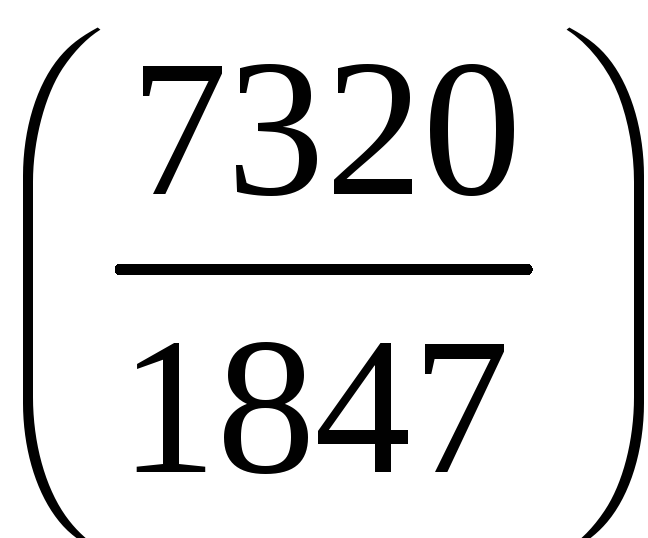 ;
і)
;
і)
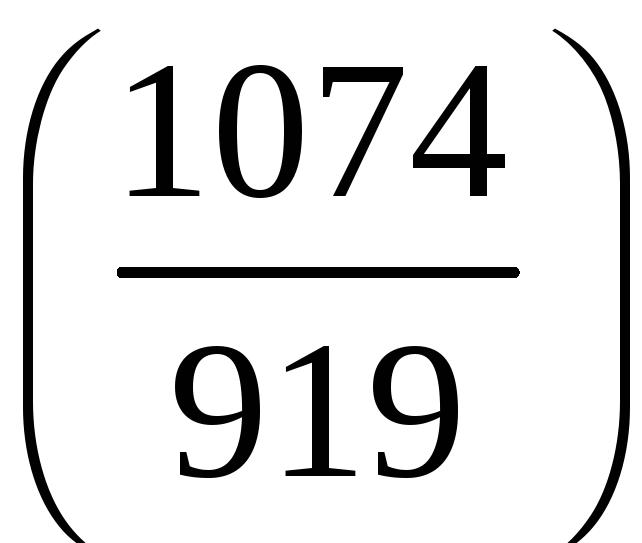 .
.
2. Розв‘язати конгруенції, звівши їх до двочленних:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
є)
![]() ;
;
3. Розв‘язати в цілих числах рівняння:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Задачі рекомендовані для розв‘язування дома
1. Знайти значення символу Лежандра:
а)
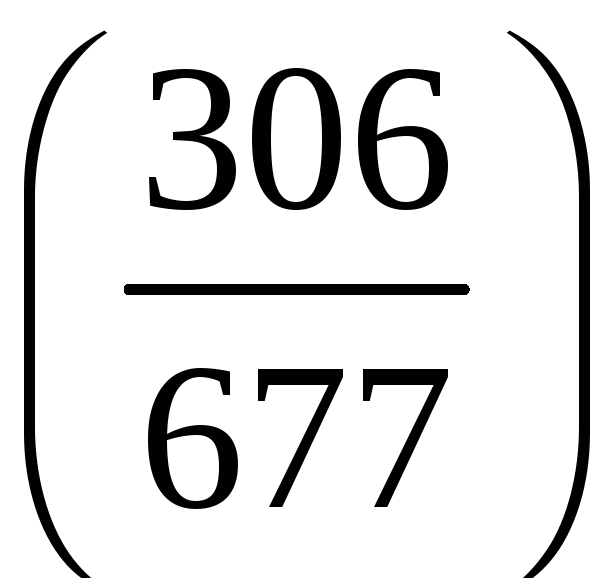 ;
б)
;
б)
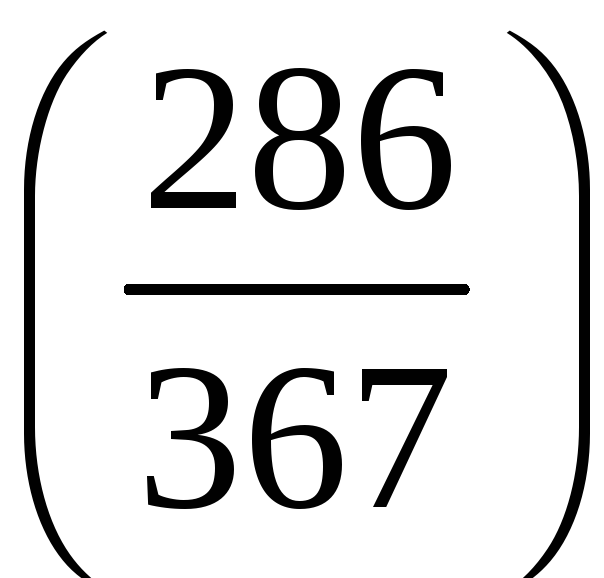 ;
в)
;
в)
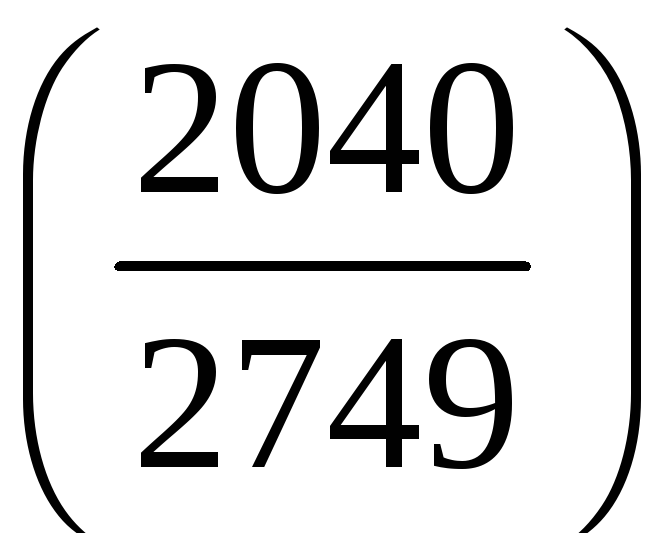 ;
г)
;
г)
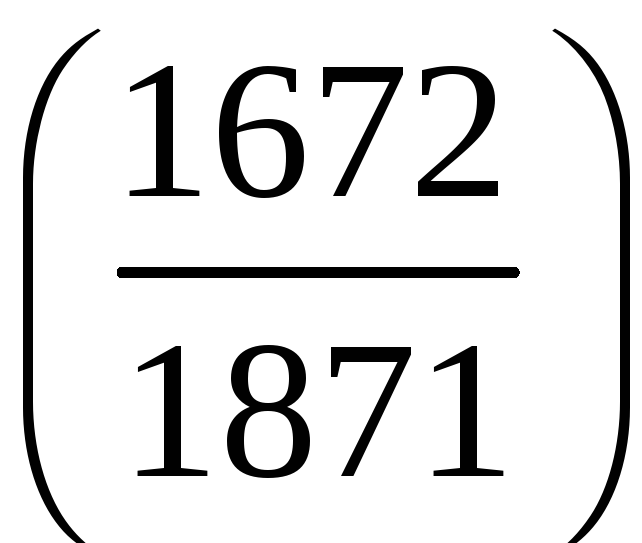 ;
д)
;
д)
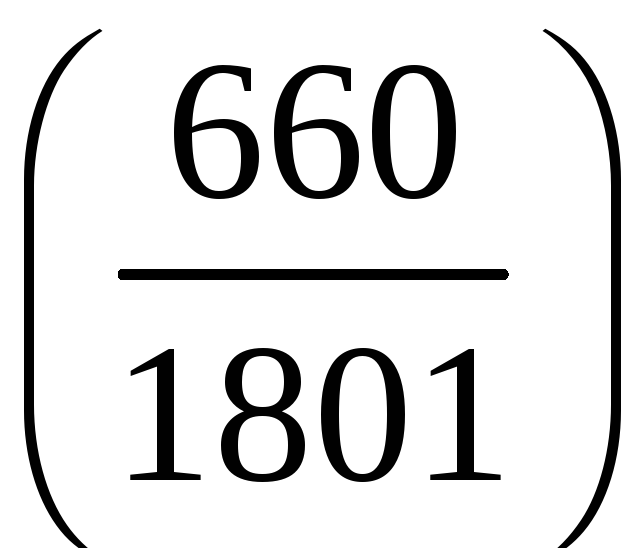 ;
;
е)
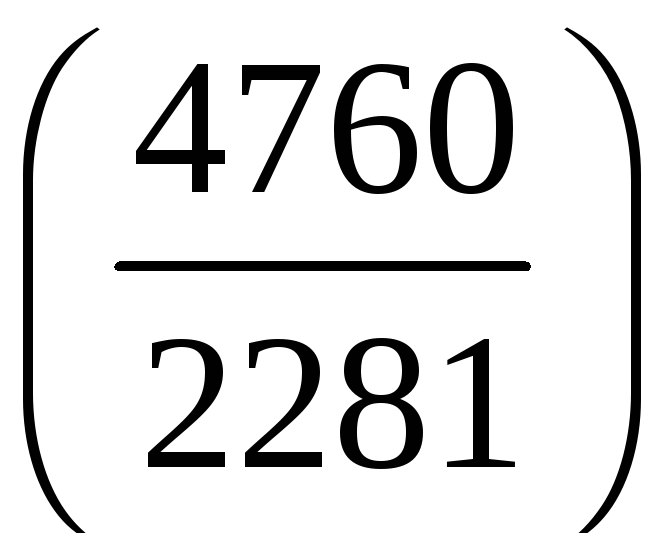 ;
є)
;
є)
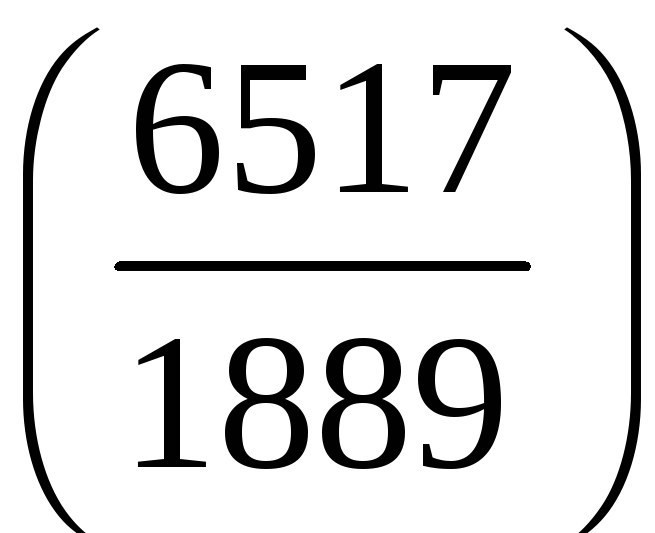 ;
ж)
;
ж)
 ;
з)
;
з)
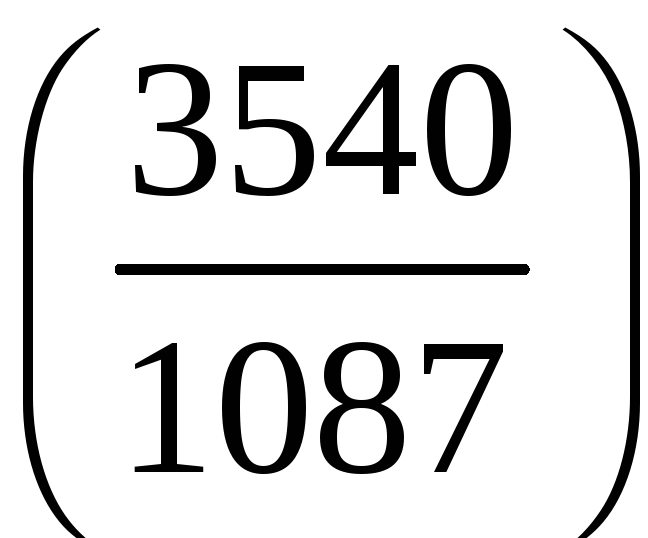 ;
і)
;
і)
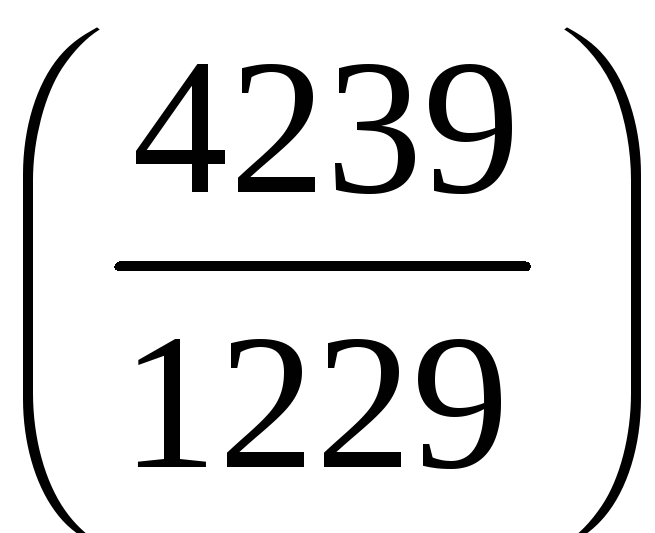 ;
;
к)
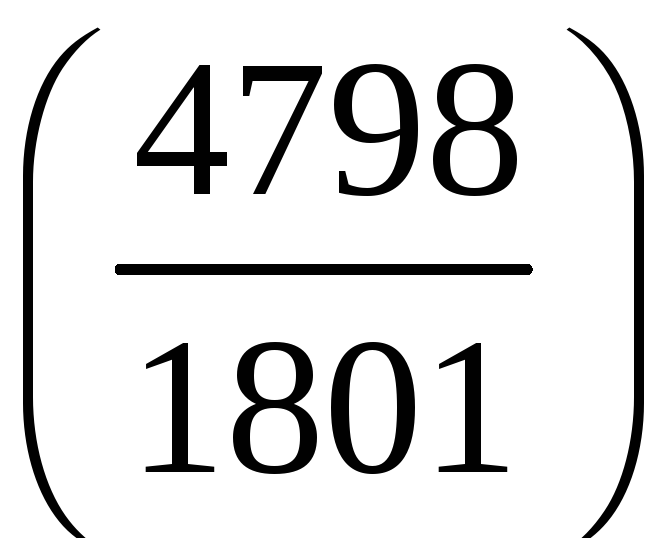 ;
л)
;
л)
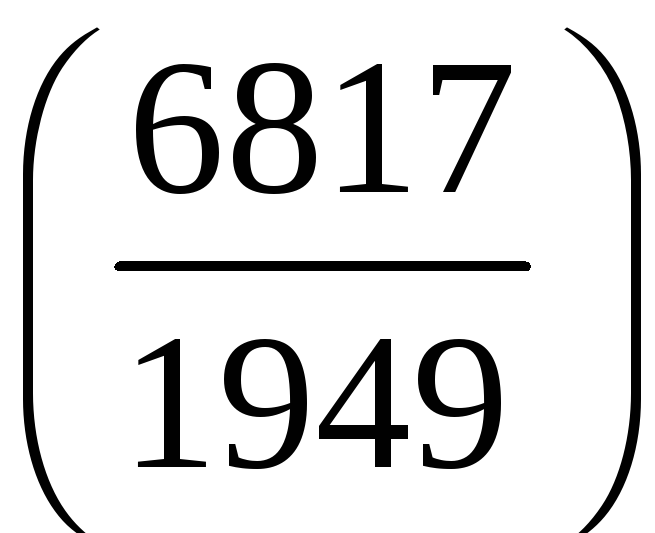 ;
м)
;
м)
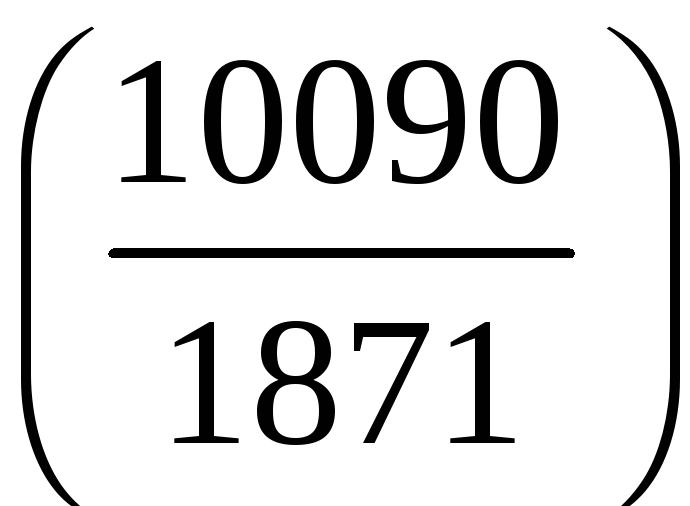 .
.
2. Розв‘язати конгруенції, звівши їх до двочленних:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
є)
![]() ;
;
ж)
![]() ;
;
з)
![]() .
.
3. Розв‘язати в цілих числах рівняння:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Модуль 3
Практичне заняття 3
Конгруенції другого степеня за складеним модулем.
Символ Якобі
Основні теоретичні відомості
Конгруенція другого степеня за складеним модулем:
![]() ,
де
,
де
![]() (1)
(1)
досліджується і розв‘язується згідно з загальними вказівками за теоремою:
Якщо
![]() попарно взаємно прості числа, то
конгруенція
попарно взаємно прості числа, то
конгруенція
![]() (*)
(*)
еквівалентна системі конгруенцій:
 (**)
(**)
При цьому, позначаючи через
![]()
числа
розв‘язків окремих конгруенцій (**)
за відповідними модулями і через
![]() число розв‘язків конгруенції (*),
матимемо:
число розв‘язків конгруенції (*),
матимемо:
![]() .
.
Висновок 1. Якщо хоч одна з конгруенцій системи (**) не має розв‘язків, то й задана конгруенція (*) також не матиме розв‘язків.
Висновок 2. Дослідження і розв‘язування конгруенції
![]() ,
,
де
![]() канонічний розклад модуля
канонічний розклад модуля
![]() ,
зводиться до дослідження і розв‘язування
конгруенцій:
,
зводиться до дослідження і розв‘язування
конгруенцій:
![]() .
Це випливає з того, що числа
.
Це випливає з того, що числа
![]() попарно взаємно прості.
попарно взаємно прості.
За зазначеною теоремою, конгруенція (1) еквівалентна системі конгруенцій
 (2)
(2)
Теорема
2.
Конгруенція
![]() має два розв‘язки або не має жодного
залежно від того, чи буде число
має два розв‘язки або не має жодного
залежно від того, чи буде число
![]() квадратичним лишком або нелишком за
модулем
квадратичним лишком або нелишком за
модулем
![]() ,
тобто чи буде відповідно
,
тобто чи буде відповідно
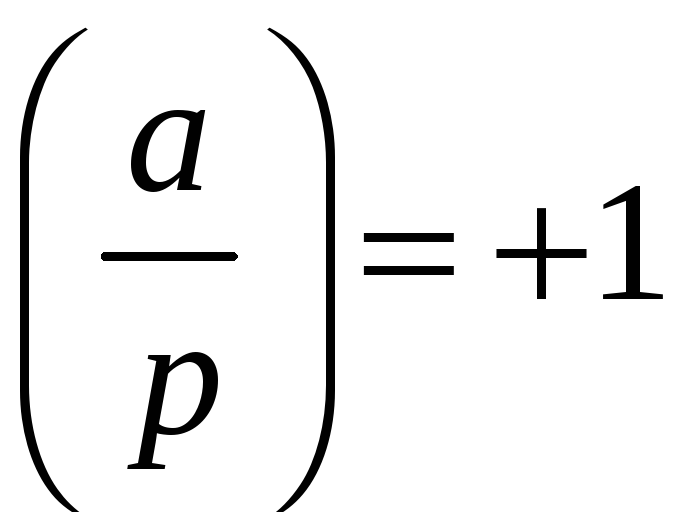 або
або
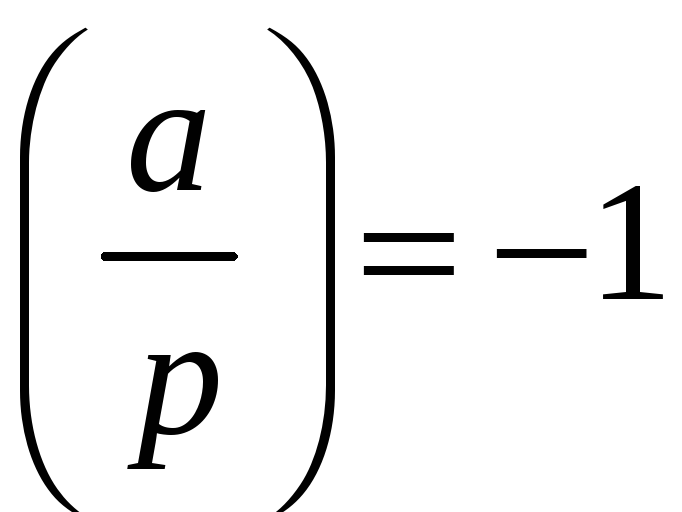 .
.
Теорема
3.
1) Конгруенція
![]() завжди має один розв‘язок при
завжди має один розв‘язок при
![]() ;
2) два розв‘язки – при
;
2) два розв‘язки – при
![]() ,
і
,
і
![]() і жодного при
і жодного при
![]() і
і
![]() ;
3) при
;
3) при
![]() конгруенція
конгруенція
![]() має розв‘язки тільки при
має розв‘язки тільки при
![]() і при цьому чотири різних розв‘язки;
два з них неодмінно задовольняють і
конгруенцію
і при цьому чотири різних розв‘язки;
два з них неодмінно задовольняють і
конгруенцію
![]() .
(3)
.
(3)
Теорема 4. Конгруенція
![]() (***)
(***)
має розв‘язок тоді і тільки тоді, коли
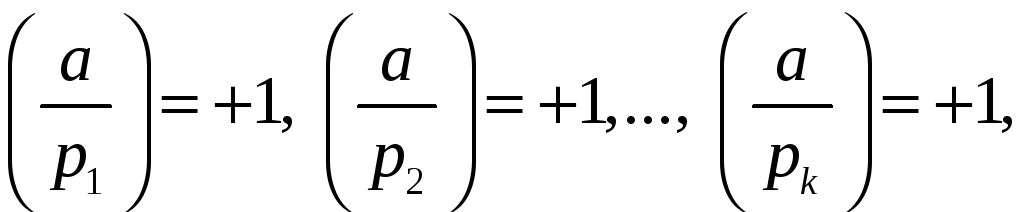
![]() при
при
![]() ,
,
![]() при
при
![]() .
.
Якщо жодну з цих умов не порушено, то кількість розв‘язків буде
![]() при
при
![]() ,
,
![]() при
при
![]() ,
,
![]() при
при
![]() .
.
Теорема
5.
Якщо
![]() задовольняє конгруенцію за простим
модулем
задовольняє конгруенцію за простим
модулем
![]() :
:
![]() ,
,
де
![]() ,
,
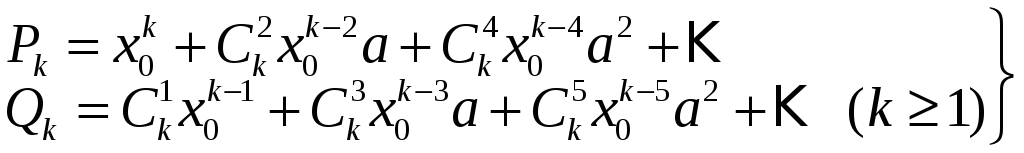 ,
(4)
,
(4)
то
![]() і розв‘язок конгруенції
і розв‘язок конгруенції
![]() (5)
(5)
має
вигляд
![]() ,
де
,
де
![]() розв‘язок конгруенції
розв‘язок конгруенції
![]() .
.
Рівняння
Пелля
мають вигляд
![]() ,
де
,
де
![]() не є точним квадратом числа.
не є точним квадратом числа.
Якщо
розкласти
![]() у неперервний дріб, то дістанемо
нескінченний періодичний дріб.
Використаємо теорему
у неперервний дріб, то дістанемо
нескінченний періодичний дріб.
Використаємо теорему
![]() .
Рівняння Петля нагадує нам залежність
між знаменниками і чисельниками підхідних
дробів, виражену вище згаданою теоремою.
З правої сторони у теоремі буде стояти
одиниця тоді, коли
.
Рівняння Петля нагадує нам залежність
між знаменниками і чисельниками підхідних
дробів, виражену вище згаданою теоремою.
З правої сторони у теоремі буде стояти
одиниця тоді, коли
![]() буде непарним числом
буде непарним числом
![]() ;
;
![]() .
Звідси видно, що рівняння Петля будуть
задовольняти чисельники і знаменники
підхідних дробів непарного порядку.
.
Звідси видно, що рівняння Петля будуть
задовольняти чисельники і знаменники
підхідних дробів непарного порядку.
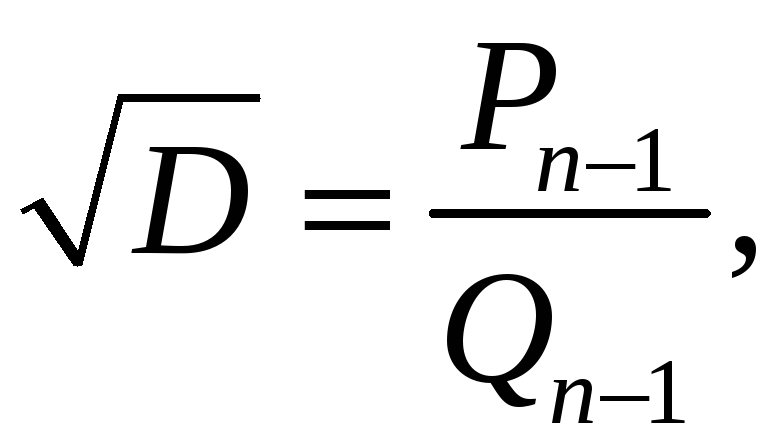
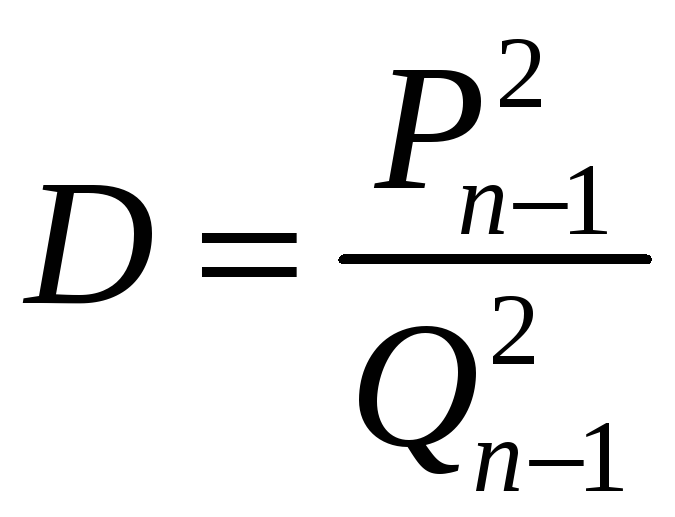 .
На цій основі можна прийняти
.
На цій основі можна прийняти
![]() і
і
![]() .
.
Методичні рекомендації до розв‘язування задач
Приклад
1.
Розв‘язати
конгруенцію
![]() .
.
Розв‘язання.
За теоремою 3, конгруенція
![]() при
при
![]() має чотири різні розв‘язки тільки при
має чотири різні розв‘язки тільки при
![]() ;
два з них неодмінно задовольняють і
конгруенцію
;
два з них неодмінно задовольняють і
конгруенцію
![]() .
.
При
![]() конгруенція
конгруенція
![]() матиме розв‘язки:
матиме розв‘язки:
![]() і
і
![]() .
Отже, спочатку знаходимо розв‘язки
конгруенції
.
Отже, спочатку знаходимо розв‘язки
конгруенції
![]() ,
а потім методом випробування визначаємо
розв‘язки
,
а потім методом випробування визначаємо
розв‘язки
![]() і
і
![]() конгруенції за модулем
конгруенції за модулем
![]() .
Поступово степінь модуля підвищуємо і
приходимо до розв‘язку конгруенції
.
Поступово степінь модуля підвищуємо і
приходимо до розв‘язку конгруенції
![]() .
.
Методом
проб знаходимо один із розв‘язків даної
конгруенції:
![]() (
(![]() ).
Другим розв‘язком буде:
).
Другим розв‘язком буде:
![]() .
(
.
(![]() ).
).
Третій
і четвертий розв‘язки знаходимо за
формулами:
![]()
![]() ,
,
![]() .
.
Остаточно
![]() ,
,
або
![]() .
.
Приклад
2.
Розв‘язати конгруенцію
![]() .
.
Розв‘язання.
Конгруенція
![]() має розв‘язок
має розв‘язок
![]() .
.
Взявши
![]() ,
,
![]() ,
обчислимо:
,
обчислимо:
![]() ,
,
![]() .
.
Розв‘язуючи
конгруенцію
![]() ,
знаходимо
,
знаходимо
![]() ,
тому
,
тому
![]() .
.
Відповідь:
![]() .
.
Приклад 3. Визначити, чи має розв‘язки конгруенція
![]() ,
,
і якщо має, то скільки.
Розв‘язання.
Знаходимо канонічний розклад модуля;
маємо:
![]() ;
далі
;
далі
![]() [теорема
3].
[теорема
3].
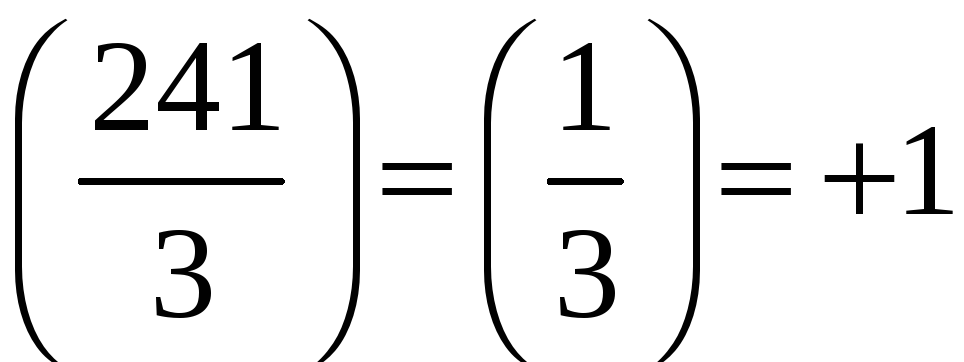 ;
;
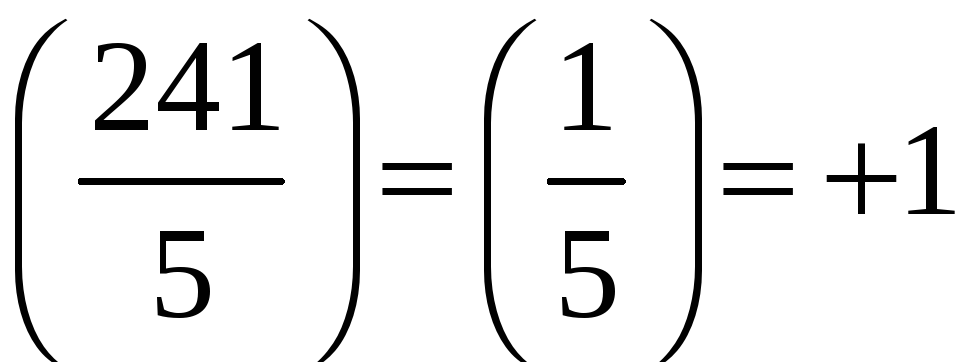 .
.
Отже,
ця конгруенція має
![]() розв‘язків, бо тут
розв‘язків, бо тут
![]() [теорема
4].
[теорема
4].
Приклад
4.
Розв‘язати
рівняння
![]() в цілих числах.
в цілих числах.
Розв‘язання.
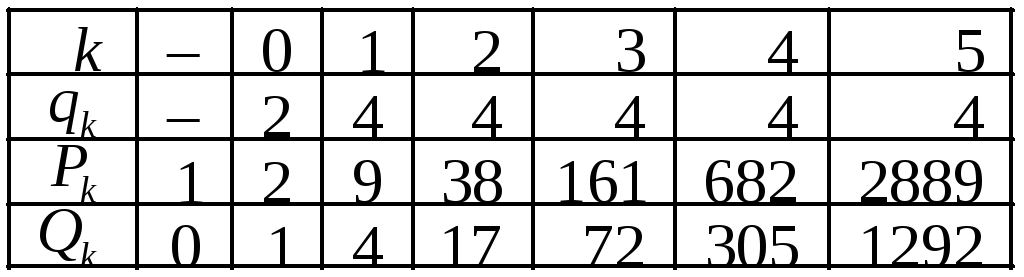
Розкладемо у ланцюговий дріб число
![]() і складемо таблицю для відшукання
і складемо таблицю для відшукання
![]() .
.
![]() .
.
 .
.
Чисельники
і знаменники підхідних дробів непарного
порядку набувають значень:
![]() ,
,
![]() ,
де
,
де
![]()
Отже,
рівняння
![]() має розв‘язки:
має розв‘язки:
![]() .
.
Задачі рекомендовані для розв‘язування в аудиторії
1. Звести такі квадратичні конгруенції до двочленних:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
2.
Показати,
що конгруенція
![]() має
два розв‘язки.
має
два розв‘язки.
3. Розв‘язати конгруенції:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
.
Задачі рекомендовані для розв‘язування дома
1. Показати, що конгруенції мають розв‘язки:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
2. Розв‘язати конгруенції:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
є)
![]() ;
ж)
;
ж)
![]() .
.
Модуль 3
Практичне заняття 4
Індекси за простим модулем.
Двочленні конгруенції за простим модулем.
Основні теоретичні відомості
