§ 13. Центр поверхні другого порядку

Означення 13.1. Точка О називається центром по­верхні другого порядку, якщо разом з довільною то­чкою М цієї поверхні їй належить і точка М´ симет­рична відносно точки О.

Нехай у деякій системі координат поверхня дру­гого порядку задана загальним рівнянням

a₁₁х² + а.₂₂у² + а.₃₃z² + 2а₁₂ху + 2a_l3xz+

+ 2а₂₃уz + 2а₁₄х + 2а₂₄у + 2а₃₄z + а₄₄ = 0 (2)

Рис. 33 Точка 0(x₀; у₀; z₀) буде центром даної поверхні тоді

і тільки тоді, коли вона буде серединою будь-якої хор­ди, яка проходить через неї. Це означає, що всі діаметральні площини поверхні проходять через точку О, тому координати точки О задоволь­няють рівняння довільної діаметральної площини (рис.33):

lF₁(х₀; y₀; z₀)+ mF₂(x₀; у₀; z₀) + nF₃(х₀.; y₀; z₀)= 0. (43)

Отже, точка O(x₀; y₀; z_Q) буде центром даної поверхні тоді і тільки тоді, коли при довільних l, m, n виконується рівність (43). А це можливо тоді і тільки тоді, коли виконуються рівності

Отже, щоб знайти центр поверхні (2), необхідно розв'язати сис­тему рівнянь:

або

Приклад 1. Знайти центр еліпсоїда

Розв'язання. Для еліпсоїда тому система

(45) записується у вигляді

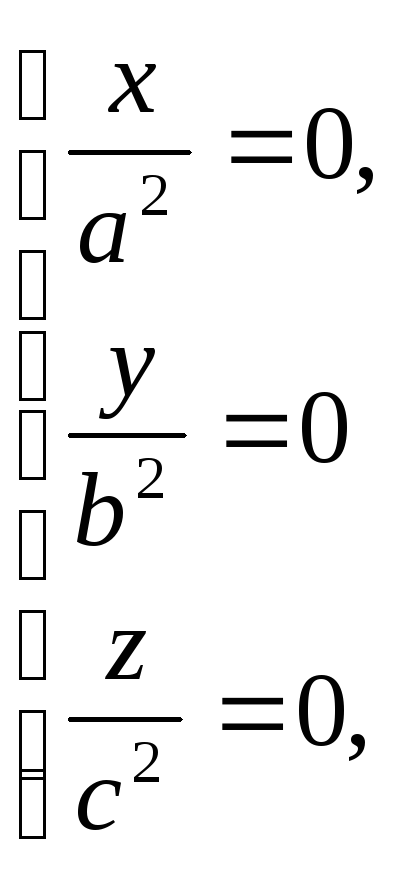
Отже, ми переконалися, що точка О(0; 0; 0) є єдиним центром еліпсоїда, заданого канонічним рівнянням. Приклад 2. Знайти центр гіперболічного циліндра

Розв'язання. Для цієї поверхні.

Із формули (45) маємо:

а це є рівняння координатної осі OZ. Отже, гіперболічний циліндр має пряму центрів. Приклад 3. Знайти центр поверхні

х² -2ху + у² + х -у = 0.

Розв'язання. Зауважимо, що це - вироджена поверхня другого І порядку, що розпадається на пару паралельних площин:

(x-y)²+(x-y)=0

(x-y)(x-y+1)=0

Для цієї поверхні , .

За формулами (45) маємо:

2x-2y+1=0

Отже, ця поверхня має площину центрів.

Приклад 4. Знайти центр гіперболічного параболоїда

Розв'язання. Перепишемо рівняння так:

Тоді За формулами (45) маємо:

Система розв'язків не має, отже, гіперболічний параболоїд не має центра.

Якщо система (45) має тільки один розв'язок, а відповідно по­верхня (2) має тільки один центр, то вона називається централь­ною. До таких поверхонь належать еліпсоїд, однопорожнинний і двопорожнинний гіперболоїди, конус.

Якщо ж ця система має безліч розв'язків, то можливі два випадки:

1. Ця поверхня має лінію центрів, тобто всі її центри розміщені на прямій. Це буде тоді, коли одне рівняння системи (45) є наслідком двох інших рівнянь. Відповідними поверхнями є еліптичний і гіпер­болічний циліндри, пара площин, що перетинаються.

2. Якщо два рівняння системи (45) є наслідками третього рів­няння, то тоді поверхня має площину центрів. Такою поверхнею є пара паралельних площин.

Якщо поверхня не має центра, то вона називається нецентральною. Такими поверхнями є еліптичний і гіперболічний параболоїди.

§ 14. Дотична площина до поверхні другого порядку

Нехай поверхня другого порядку задана загальним рівнянням

a₁₁х² + а.₂₂у² + а.₃₃z² + 2а₁₂ху + 2a_l3xz+

+ 2а₂₃уz + 2а₁₄х + 2а₂₄у + 2а₃₄z + а₄₄ = 0. (2)

а точка P₀(x₀; y₀ ;z₀) лежить на цій поверхні.

Теорема 7.5. Геометричне місце прямих, які проходять через точ­ку Р₀ і дотикаються до поверхні в цій точці, є площиною. Ця пло­щина називається дотичною площиною до поверхні в точці Р₀.

Доведення. Запишемо рівняння деякої прямої, що проходить че­рез точку Р₀(х₀; у₀; z₀):

(35)

Знайдемо координати точок перетину поверхні (2) і прямої (35). Для цього підставимо (35) в (2) і скористаємося позначен­нями, введеними в § 12. Матимемо:

(a₁₁l²/+ a₂₂m²+ a₃₃n² +2a₃₂lm+2a_nln + 2a₃₃mn)t²+ 2(lF₁(х₀,y₀,z₀) +

+mF₂(х₀,y₀,z₀) +nF₃(х₀,y₀,z₀))t +F(х₀,y₀,z₀)=0 (46)

Оскільки точка Р₀(х₀; y₀; z₀) лежить на поверхні (2), то F(x₀; y₀; z₀)=0 і рівняння (46) запишеться у вигляді

(a₁₁l²+а₂₂т² + а₃₃п²+2a₁₂lm -2a₁₃ln +2a₂₃mn)t² +

+2(lF₁(х₀,y₀,z₀) +mF₂(х₀,y₀,z₀) +nF₃(х₀,y₀,z₀))t =0. (47)

Пряма (35) дотикається до поверхні (2) у точці Р₀(x₀; y₀; z₀) тоді і тільки тоді, коли це квадратне рівняння має два корені t= 0, які збігаються, тобто коли

lF₁(х₀,y₀,z₀) +mF₂(х₀,y₀,z₀) +nF₃(х₀,y₀,z₀)=0 (43)

Виключаючи l, m, n з (35) і (43), ми замінюємо координати напрямних векторів дотичних прямих пропорційними їм різницями

x-х₀ ;у-у₀, z-z₀ ,які містять змінні координати точок дотичних., тобто знаходимо рівняння геометричного місця дотичних:

(х- х₀ )F₁(х₀,y₀,z₀) +( у-у₀) F₂(х₀,y₀,z₀) +( z-z₀) F₃(х₀,y₀,z₀)=0.

F₁(х₀,y₀,z₀)x+ F₂(х₀,y₀,z₀)y+ F₃(х₀,y₀,z₀)z-

-( х₀F₁(х₀,y₀,z₀) + y₀F₂(х₀,y₀,z₀) + z₀F₃(х₀,y₀,z₀))=0 (48)

Перетворимо вираз у дужках. Оскільки

F(x; у; z) = xF₁ (х; y; z) + yF₂{x; у; z) + zF₃{x; y; z) + F₄{x; у; z),

де

F₄(x; y; z) = а₄₁х + а₄₂у + а₄₃z + а,₄₄,

то

х₀F₁(х₀,y₀,z₀) + y₀F₂(х₀,y₀,z₀) + z₀F₃(х₀,y₀,z₀)= F(x₀; y₀; z₀) - -F₄(x₀; у₀; z₀)= -F₄(x₀; y₀; z₀).

Підставивши у (48), матимемо

F₁(х₀,y₀,z₀)x+ F₂(х₀,y₀,z₀)y+ F₃(х₀,y₀,z₀)z+ F₄(x₀; у₀; z₀)=0 (49) або

(а₁₁х₀ + а₁₂у₀ + a₁₃z₀ + a₁₁)x + (a₃₁х₀ +a₂₂y ₀+a₂₃z₀ + a₃₄ )у +

+ (а₃₁х₀ +а₃₂у₀ + a₃₃z₀ +а₃₄)z + (а₄₁х₀ + а₄₂y₀ + а₄₃z₀ + а₄₄) = 0. (50)

Це рівняння лінійне. Отже, геометричне місце дотичних до поверх­ні другого порядку в точці Р₀ є площина. Теорему доведено.

Рівняння (49), (50) - рівняння дотичної площини до поверхні (2) у точці P₀(x₀; y₀; z₀)

Приклад 1. Записати рівняння дотичної площини до еліпсоїда

у його точці P₀(ч₀; y₀; z₀).

Розв'язання. Для еліпсоїда

За формулою (49)

або

Приклад 2. Записати рівняння дотичної площини до еліптичного параболоїда у його точці Р₀(x₀; y₀; z₀).

Розв'язання. Для цієї поверхні

За формулою (49)

або

Пропонуємо самостійно переконатися, що дотичною площиною у точці Р₀(x₀; у₀; z₀):

- до однопорожнинного гіперболоїда є площина

- до двопорожнинного гіперболоїда площина

- до гіперболічного параболоїда площина

до конічної поверхні площина