§ 9. Еліптичний параболоїд

Означення 9.1. Еліптичним параболоїдом називається поверхня, яка в деякій прямокутній системі координат задається рівнянням

(24)

Це рівняння називають канонічним рівнянням еліптичного параболоїда.

З цього рівняння випливають такі властивості елішпичного параболоїда:

1. Еліптичний параболоїд проходить через початок координат, і це єдина точка, в якій він перетинає координатні осі.

2. Еліптичний параболоїд симетричний відносно координатних площин OXZ, OYZ, оскільки разом із точкою (х; у;z ) його рівняння задовольняють точки (х; -у; z), (-x; у; z), симетричні відносно цих площин.

3. Еліптичний параболоїд симетричний відносно осі OZ, бо ця вісь є лінією перетину його площин симетрії. Вісь OZ називається віссю еліптичного параболоїда, а точка, в якій він перетинає цю вісь, -вершиною.

4. Якщо еліптичний параболоїд перетнути площинами z = h, h > 0, паралельними до площини ОXY, то в перетині утворяться еліпси

Рис. 25

або

Розміри цих еліпсів збільшуються зі збільшенням h (рис. 25). Якщо еліптичний параболоїд перетнути площинами у = h, паралельними до площини OXZ, то в перетині утворяться параболи

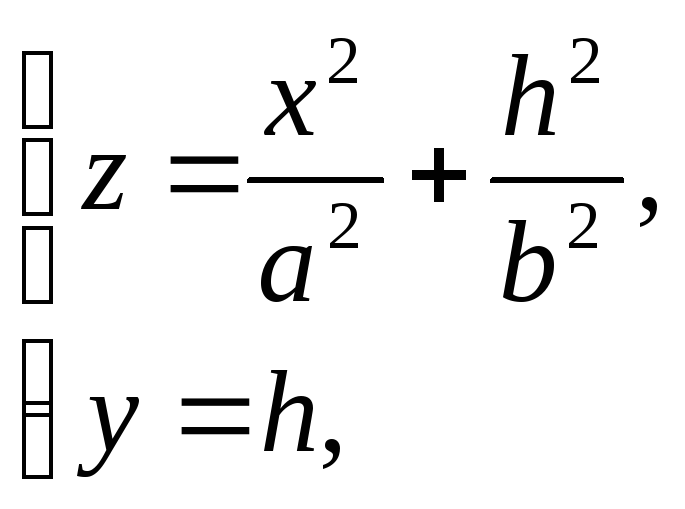(25)

осі яких паралельні до осі OZ.

Якщо еліптичний парабалоїд перетнути площинами х = h, паралельними до OYZ, то в перетині утворяться параболи

осі яких паралельні до осі OZ.

Зокрема, в перерізі з площиною OYZ утвориться парабола

(26)

Координати вершини параболи (25)

задовольняють рівняння (26). Тому еліптичний параболоїд може бути утворений в результаті руху параболи (25), площина якої паралельна до площини OXZ так, щоб її вершина рухалась по параболі (26), площина якої перпендикулярна до площин, в яких лежать перші параболи.

Зауваження. Якщо в рівнянні еліптичного параболоїда а = b, тобто

то одержимо параболоїд обертання, який утворюється з параболи

обертанням її навколо осі OZ.

Якщо рівняння еліптичного параболоїда

z

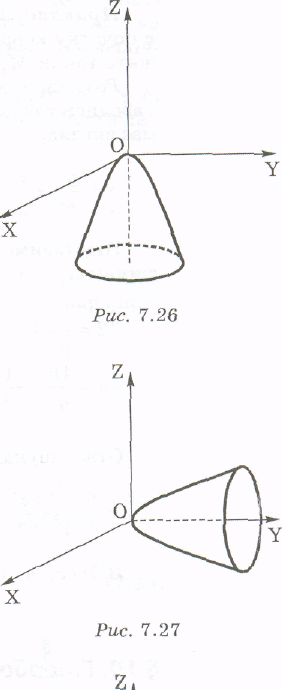
то він розташований в іншому півпросторі відносно площини OXY, ніж еліптичний параболоїд (24) (рис. 26).

Еліптичний параболоїд, заданий рівнянням

y=

матиме своєю віссю вісь OY (рис. 27).

Якщо еліптичний параболоїд має рівняння

то його віссю буде вісь ОХ (рис. 28).

Рис. 28

Приклад. Знайти рівняння еліптичного параболоїда з вершиною в початку координат, вісь якого збігається з віссю ОХ і якому належать точки М₁(2; -2; 1) і М₂(5; 4; -1).

Розв'язання. Оскільки віссю еліптичного параболоїда є пряма ОХ і абсциси точок на його поверхні додатні, то його канонічне рівняння має вигляд:

Підставимо координати даних точок у це рівняння і розв'яжемо систему;

.

Отже, шукане рівняння має вигляд

Відповідь. x=