
- •§ 7. Однопорожнинний гіперболоїд
- •§8. Двопорожнинний гіперболоїд
- •§ 9. Еліптичний параболоїд
- •§ 10. Гіперболічний параболоїд
- •§ 11. Прямолінійні твірні на поверхні другого порядку
- •11.1. Прямолінійні твірні на поверхні однопорожнинного гіперболоїда
- •11.2. Прямолінійні твірні гіперболічного параболоїда
- •§ 12. Діаметральні площини поверхні другого порядку
- •§ 13. Центр поверхні другого порядку
- •§ 14. Дотична площина до поверхні другого порядку
- •§ 15. Площини симетрії поверхні другого порядку
- •§ 16. Зведення загального рівняння поверхні другого порядку до канонічного вигляду
§ 7. Однопорожнинний гіперболоїд
Означення 7.1. Однопорожнинним гіперболоїдом називається поверхня, яка в деякій прямокутній системі координат задається рівнянням
![]() (19)
(19)
Це рівняння називається канонічним рівнянням однопорожнинного гіперболоїда, а система координат, в якій воно задане, - канонічною системою координат.
Властивості однопорожнинного гіперболоїда.
Аналізуючи рівняння (19), встановлюємо такі властивості даної поверхні:
1 Однопорожнинний гіперболоїд не проходить через початок координат.
2. Однопорожнинний гіперболоїд не перетинає вісь OZ, а дві інші осі перетинає в точках, симетричних відносно початку координат, а саме:
Якщо
![]() <
b,
то
уявною віссю такої гіперболи є вісь OZ
<
b,
то
уявною віссю такої гіперболи є вісь OZ
Якщо
![]() >
b,
то
уявною віссю є вісь ОХ.
>
b,
то
уявною віссю є вісь ОХ.
Якщо
![]() = b,
то
в перерізі утворяться дві прямі,
= b,
то
в перерізі утворяться дві прямі,
що
перетинаються: z
= ±
![]() (рис. 20).
(рис. 20).
Аналогічні перерізи утворюються і при перетині однопорожнинного гіперболоїда площинами, паралельними до площини OYZ.
Розглянемо поряд з однопорожнинним гіперболоїдом (17) конічну поверхню, задану рівнянням
![]()
Ця поверхня не перетинається з однопорожнинним гіперболоїдом, бо система рівнянь несумісна

Рис. 20
Оскільки цей конус проходить через початок координат, який міститься всередині однопорожнинного гіперболоїда, то і весь конус міститься всередині однопорожнинного гіперболоїда. Якщо обидві поверхні перетнути площиною OXZ, рівняння якої у = 0, то в перетині з гіперболоїдом дістанемо гіперболу

а в
перетині з конусом - дві прямі: z
= ±
![]() ,
які будуть асимптотами цієї гіперболи
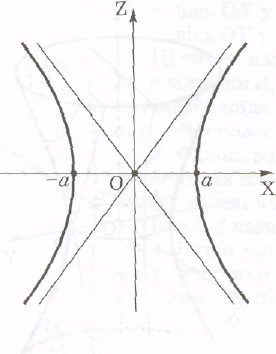
(рис. 21). Можна показати, що ця властивість
конуса, пов'язана з однопорожнинним
гіперболоїдом, справедлива і при перетині
будь-якою іншою площиною, що проходить
через вісь OZ.
,
які будуть асимптотами цієї гіперболи
(рис. 21). Можна показати, що ця властивість
конуса, пов'язана з однопорожнинним
гіперболоїдом, справедлива і при перетині
будь-якою іншою площиною, що проходить
через вісь OZ.
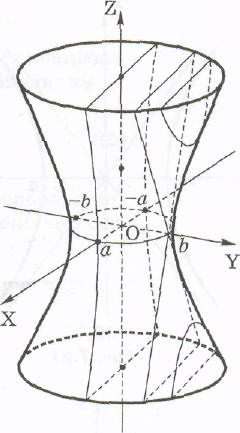
У зв'язку з цим даний конус називають асимптотичним конусом однопорожнинного гіперболоїда (рис. 22).
Рівняння
![]() =
1 і
=
1 і
![]()
також задають однопорожнинні гіперболоїди з головною віссю ОY та ОХ відповідно.
Приклад. Записати канонічне рівняння однопорожнинного гіперболоїда, якщо він перетинає площину OXY по колу x2 + у2 = 9, а площину OXZ - по
гіперболі![]() =
1.
=
1.
Рис.21
Розв'язання. Однопорожнинний гіперболоїд перетинає площину OXY по колу, тому його головною віссю є вісь OZ, а його рівняння має вигляд:
![]()
 (21)
(21)
Ця
поверхня перетинається з площиною OXY
по еліпсу
![]() = 1 • Зіставляючи з даною лінією перетину
= 1 • Зіставляючи з даною лінією перетину
x2+y2=9,
або
![]() дістанємо:
a2=b2=9.
дістанємо:
a2=b2=9.
Тоді рівняння (21) набуде вигляду:
![]()
Рис.22
За умовою
ця поверхня перетинається з площиною
OXZ
по гіперболі
![]() звідки
випливає, що c2=10.
Отже рівняння даного одно порожнинного
гіперболоїда
звідки
випливає, що c2=10.
Отже рівняння даного одно порожнинного
гіперболоїда
![]()
Відповідь.
![]()
