Тема 5. Плоское движение твердого тела.

П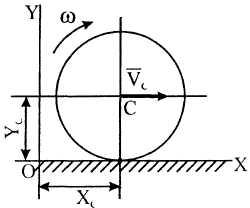ример 17. Колесо радиуса катится по прямолинейному горизонтальному рельсу с постоянной угловой скоростью (рис. 14). Записать уравнения плоского движения колеса, если центр колеса имеет постоянную скорость: .

Р

Рисунок 14

ешение. Так как колесо движется равномерно, то координата центра колеса по оси будет равна: . Координата центра колеса по оси постоянна и равна радиусу: . Угол поворота колеса при равномерном вращении равен: .

Ответ. ; ; .

П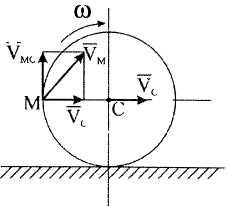ример 18. Определить скорость точки обода колеса, используя условие примера 17.

Решение. Применим формулу (3). За полюс примем точку , скорость которой известна:

В

Рисунок 15

ращательная скорость точки относительно полюса равна: . Вектор перпендикулярен отрезку и направлен в соответствии с угловой скоростью. Поэтому вектор относительно полюса должен показывать направление угловой скорости (рис. 15). Так как , то , , . Ответ. .

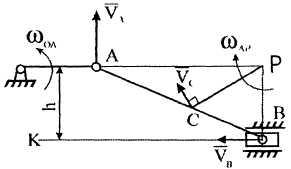Пример 19. В

Рисунок 16

положении механизма, схема которого приведена на рис. 16, определить угловую скорость шатуна и скорости точек и , если , , , , .

Решение. Найдем скорость точки :, .

Скорость ползуна должна быть направлена по прямой . Мгновенный центр шатуна находится в точке пересечения перпендикуляров, восстановленных к направлениям векторов скоростей точек и . Угловая скорость шатуна равна:

Определим величины , , . , , , . Тогда равносторонний: . Находим: , , .

Направление угловой скорости шатуна определяется по направлению вращения вектора скорости точки относительно мгновенного центра скоростей. Угловая скорость шатуна направлена по часовой стрелке. Скорости точек и должны показывать такое же направление. Для построения вектора восстанавливаем перпендикуляр к отрезку и направляем вектор в соответствии с направлением .

Ответ. , .

П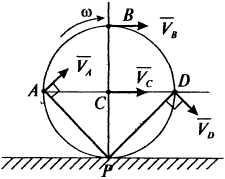ример 20. Колесо катится без скольжения по прямолинейному рельсу. Скорость центра колеса равна 20м/с, Радиус колеса 1м. Найти скорости точек , , и угловую скорость колеса (рис. 17).

Р

Рисунок 17

ешение. Мгновенный центр скоростей находится в точке соприкосновения колеса и неподвижной поверхности:

Угловая скорость направлена по часовой стрелке. Определим расстояние точек , , до МЦС:

, , , .

Вектор перпендикулярен прямой , а вектор перпендикулярен прямой . Вектор перпендикулярен . Направления векторов , , должны соответствовать угловой скорости колеса (рис. 17).

Ответ. , .

П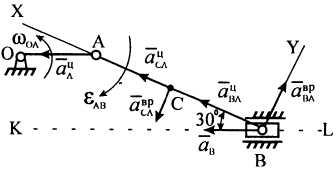ример 21. Используя условие примера 19, определить ускорение точек и (рис. 18).

Решение. За полюс выберем точку , так как ускорение этой точки можно найти:

Рисунок 18

, ,

так как кривошип вращается равномерно, . . Вектор направлен по от точки к точке .

Применим формулу , задавая направление вектора (рис. 18):

Находим и : , так как неизвестно, то зададим направление вектора , учитывая, что . .

Вектор направлен по от точки к полюсу . Запишем проекции на оси координат (X, У): Ось Х: Ось Y:

Находим и .

Минус показывает, что вектор направлен в сторону, противоположную направлению, выбранному на рис. 18. Определим угловое ускорение шатуна :

.

Направление будет по часовой стрелке. Определим ускорение точки , выбрав за полюс точку . Вектор разложим по выбранным осям координат:

.

Находим и : вектор , и направлен в соответствии с . Вектор и направлен по от точки к полюсу .

Проектируем выражение на оси координат:

, ,

.

Ответ. , .

Пример 22. Колесо радиуса катится без скольжения равнозамедленно по прямолинейному горизонтальному рельсу. Скорость центра колеса . Ускорение центра . Найти ускорение точки с помощью МЦУ и по теореме об ускорениях точек плоской фигуры.

Р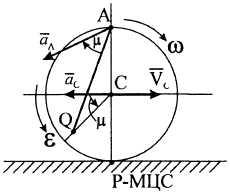ешение. Находим угловые скорость и ускорение колеса:

, .

У

Рисунок 19

гловая скорость направлена по часовой стрелке, так как вектор скорости относительно МЦС поворачивается по часовой стрелке. Угловое ускорение направлено противоположно в соответствии с направлением вектора ускорения центра колеса .

I способ. Определим угол : , .

Повернем на угол 45° по направлению углового ускорения. Определим расстояние от точки до МЦУ (рис. 19): .. Находим расстояние точки до МЦУ из : .

В точке от отрезка отложим вектор ускорения точки в направлении, противоположном угловому ускорению. Величина ускорения точки равна:

.

Ответ. .