Раздел 2. Кинематика (Примеры).

Тема 2. Кинематика точки

П

Рисунок 1

ример 1. Движение точки задано радиусом-вектором , где и — постоянные взаимно перпендикулярные векторы (рис. 1). Определить траекторию точки, а также скорость и ускорение точки при t =2 с.

Решение. Для построения траектории зададим время от 0 до 2 с и найдем величины радиуса-вектора в эти моменты времени:

Из выбранного центра отложим векторы , , (рис. 2). Траекторией движения будет прямая линия. Скорость точки равна: . При скорость точки .

В

Рисунок 2

ектор скорости будет направлен по прямой в сторону увеличения расстояния . Ускорение точки равно: . Ускорение постоянно, и вектор ускорения направлен по прямой в сторону возрастания скорости.

Пример 2. Движение точки по винтовой линии в декартовой системе координат можно задать тремя уравнениями (рис. 3): , , , где — постоянные величины; — радиус цилиндра.

Рисунок 3

Пример 3.

Движение точки задано уравнениями: , , см. Найти траекторию точки в координатной форме и задать движение точки в векторной форме (рис. 4).

Р

Рисунок 4

ешение. Исключим время из уравнений движения. Для этого возведем обе части заданных уравнений в квадрат и сложим их:

, , , или .

Т.о. траектория — окружность радиуса 4 см. Для получения радиуса-вектора используем формулу (6): .

Ответ. Траекторией точки будет окружность радиуса 4 см. Закон движения .

Пример 4. Движение точки задано уравнениями , см; , см. Найти траекторию точки в координатной форме.

Р

Рисунок 5

ешение. Преобразуем уравнения движения:

, .

При
При

Получим уравнение траектории (рис. 5). Установим границы траектории. Начало движения в точке :

Ответ. Траекторией точки будет полупрямая, ограниченная точкой (-2,1).

Пример 5.

Найти скорость и ускорение точки в любой момент времени, используя условие примера 2.

Решение. Находим скорость:

, , ,

,

, ,

, , ,

Находим ускорение: ,

,

Ответ. , .

П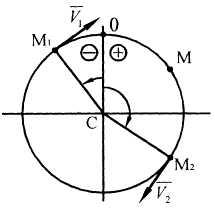ример 6. Точка движется по дуге окружности радиуса по закону . Определить скорость точки в момент времени и .

Р

Рисунок 6

ешение. Движение задано естественным способом. Примем за начало отсчета точку О, считая направление движения по часовой стрелке положительным. Находим дуговые координаты точки в заданные моменты времени:

, .

Положение точек и на траектории покажем с помощью углов (рис. 6): , .

Находим величины скорости в заданные моменты времени: ,

, . Так как , , то векторы скоростей будут направлены в сторону возрастания S по касательной к траектории (рис. 6).

Ответ. , .

Пример 8. При отходе от станции поезд, двигаясь равноускоренно по закруглению радиуса 900 м, за время достиг скорости . Определить путь, пройденный поездом и его полное ускорение.

Р

Рисунок 7

ешение. За начало отсчета примем положение поезда в момент отхода от станции (рис. 7). Начальные условия движения: , .

, , , .

Ответ. ,

Пример 9. Поезд движется со скоростью . При торможении ускорение равно . Найти время и путь торможения.

Решение. При начальных условиях движения имеем , : , . Так как поезд остановился, то , тогда . .

Ответ. , .

Пример 10. Определить ускорение точки через 2 с после начала движения из состояния покоя, если движение задано уравнениями: , .

Решение. Находим проекции скорости и ускорения на координатные оси:

, , . ,

, , , .

Ответ. , ,

Пример 11. Перейти к естественному способу задания движения, если заданы уравнения движения точки в координатной форме: а) , б) .

Решение. Для естественного способа задания необходимо знать:

1. Траекторию.

2. Закон движения.

3. Начало отсчета.

4. Положительное направление движения.

1. Траекторию движения определим, исключая время из уравнений движения а), б):

и

Рисунок 8

з а) ; из б) . Откуда получим или . Траектория представляет собой прямую линию (рис. 8), ограниченную точкой .

2. Закон движения находим по следующей формуле: , где , , .

3. Начало отсчета находим из уравнений движения, подставив в них время, равное нулю: , .

4. Положительное направление движения определим, подставив в уравнение движения время, равное 1с: , .