Тема 6.

Пример 24. Будет ли система сил, приведенная на рис. 1, статически определимой?

Р

Рисунок 1

ешение. На рис. 1 изображена плоская произвольная система сил, для которой можно составить только три независимых уравнения равновесия. Определим число неизвестных. Пользуясь принципом освобождаемости от связей, заменяем их действия реакциями. В точке А — одна реакция. На другой опоре (шарнирно-неподвижной) — две реакции: .

Число неизвестных реакций равно числу уравнений равновесия. Изображенная система сил является статически определимой.

Пример 25. Будет ли система сил, изображенная на рис. 2, статически определимой?

Р

Рисунок 2

ешение. Изображенная система сил является плоской произвольной системой сил, для которой можно составить три уравнения равновесия. Определим число неизвестных реакций. В точке А имеем две неизвестные реакции: . В точке С связью является стержень с двумя шарнирами и реакция будет направлена через точки . В точке B имеется еще одна реакция. Итого имеем четыре неизвестные реакции. Число неизвестных величин превышает число уравнений. Система, приведенная на рис. 2, будет статически неопределимой.

Пример 26. Определить реакции опор А, В и шарнира С составной балки, если M=8кН/м, q=2кН/м, Р=6кН (рис. 3).

Р

Рисунок 3

ешение. Расчленим составную балку по шарниру С и рассмотрим равновесие балки АС под действием момента M, равномерно распределенной нагрузки интенсивности q и реакций шарнирно-неподвижной опоры А, и реакций шарнира С (рис. 4). Для полученной уравновешенной плоской произвольной системы сил составим три уравнения равновесия, заменяя равномерно распределенную нагрузку силой , приложенной к середине нагруженного участка DE. Направление осей координат показано на рис. 4.

1. ,

2. ,

3. 

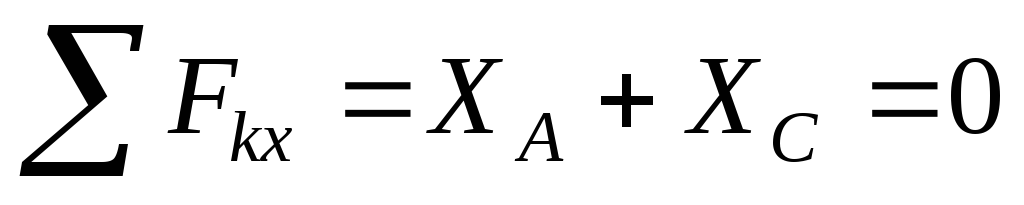   Рисунок 4

   .

Теперь рассмотрим равновесие другой части, на которую действуют сила Р, реакции шарнирно-неподвижной опоры В и реакции шарнира С (рис. 5). На основан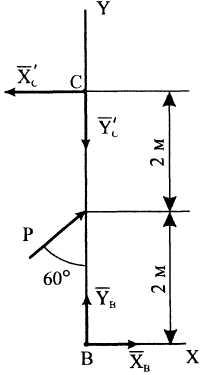ии аксиомы действия-противодействия реакции в шарнире С равны по модулю и противоположно направлены: , ,

Для полученной уравновешенной плоской произвольной системы сил составим три уравнения равновесия:

4. , 5. ,

6. .

Н

Рисунок 5

аходим из 6: , ,

из 3: , из 5: , из 2:,

из 1: .

Ответ. , , , , , .

Минус показывает, что реакции и направлены противоположно направлению, показанному на рис. 5.

Тема 7.

Пример 27. На тело, находящееся на шероховатой горизонтальной поверхности, действует сила под углом . Определить, выйдет ли тело из положения равновесия, если коэффициент трения (рис. 4).

Р

Рисунок 4

ешение. Для уравновешенной плоской системы сходящихся сил можно составить два уравнения равновесия:

1. , 2. . Находим из 2: , из 1: .

Так как , то , или . Тогда .

Подставим исходные данные и получим .

Ответ. Так как сила приложена под углом, меньшим угла трения, то тело не выйдет из положения равновесия.

П

Рисунок 5

ример 28. Тело весом 100Н удерживается на шероховатой наклонной плоскости силой (рис. 5). Коэффициент трения скольжения между телом и плоскостью . Определить значение силы при равновесии тела на плоскости, если .

Решение. Возможны два случая предельного равновесия тела и соответственно два предельных значения силы при двух направлениях силы трения: , , где — коэффициент, учитывающий направление движения, .

Составим для плоской произвольной системы сил два уравнения равновесия:

1. , 2. . Находим из 2: , тогда: . Из 1: . При , при .

Ответ. Сила при равновесии тела должна удовлетворять условию .

Пример 29. На наклонной поверхности находится цилиндр радиуса (рис. 7). Определить, при каких углах наклона плоскости к горизонту цилиндр будет находиться в равновесии, если — коэффициент трения скольжения, — коэффициент трения качения.

Р

Рисунок 7

ешение. Изобразим действующие на цилиндр силы. Силу трения скольжения направим вверх по наклонной поверхности. Момент трения качения направим по часовой стрелке, одну из осей направим по наклонной поверхности (рис. 7).

Составим три уравнения равновесия для уравновешенной плоской произвольной системы сил:

1. , 2. , 3. .

Находим из 1: , из 2: , из 3: .

Для равновесия необходимо, чтобы выполнялись следующие неравенства:

, . (6)

Подставим , , в неравенства (5):

, (7)

, (8)

Для равновесия цилиндра на наклонной поверхности необходимо, чтобы неравенства (7) и (8) выполнялись одновременно.

Если , то потеря равновесия произойдет путем перехода к качению, так как нарушится неравенство (8).

Если , то потеря равновесия произойдет за счет трения скольжения, так как нарушится неравенство (7).

13

ПРИКЛАДНАЯ МЕХАНИКА