Тема 3.

Пример 9. О

Рисунок 1

пределить момент силы F= 100 Н относительно точек А, С, В. Сила действует по диагонали прямоугольника ABCD, где ВС= 3 м, АС =4 м.

Решение. Определим плечо силы относительно точек А и В. Для этого опускаем перпендикуляр на линию действия силы (прямую CD) из точек А и В (рис. 1):

, . Из : .

, так как . , (момент силы относительно точки В отрицательный, так как сила стремится повернуться относительно точки В по ходу часовой стрелки), , так как h_C= 0.

Ответ. , , .

Пример 10. И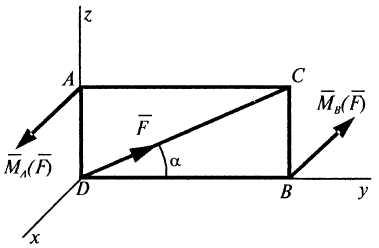спользуя условие примера 9, найти направление векторного момента точек и , если , 

Р

Рисунок 3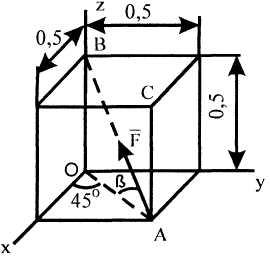

ешение. Используя определение векторного момента, можно сделать вывод, что векторный момент относительно точки направлен перпендикулярно плоскости чертежа на читателя, а относительно — в обратную от читателя сторону (рис.3).

Пример 11. Определить момент силы F=40Н относительно осей координат и относительно начала координат, если сторона куба равна 0,5 м (рис. 5).

Решение.

1-ый способ. По формуле (3) найдем проекции векторного момента на оси координат:

Рисунок 5

, , .

Найдем координаты точки А и проекции силы F на оси координат

, , , , ,

, , .

Тогда

, , , .

2-ой способ. Определим моменты силы относительно осей координат по формуле (5).

Спроектируем силу на плоскость, перпендикулярно осям X, Y, Z: , , , .

Получим

, ,

(так как пересекает ось Z, то момент силы относительно оси Z равен нулю). Результаты, полученные обоими способами, совпадают.

Ответ. , ,

, .

Тема 4.

Пример 12. Найти равнодействующую силу и точку ее приложения, если , F₁=20Н, F₂=5Н, АВ=0,4м (рис. 1).

Р

Рисунок 1

ешение. , , , , , . Ответ. , AC = 0,08 м.

Пример 13. Н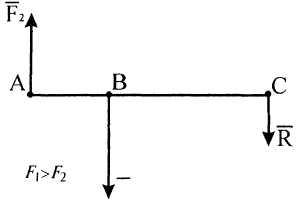айти равнодействующую силу и точку ее приложения, если , F₁=20Н, F₂=5Н, АВ=0,4м (рис. 2).

Р

Рисунок 2

ешение. , , , , , . Ответ. , BC=0,13м.

П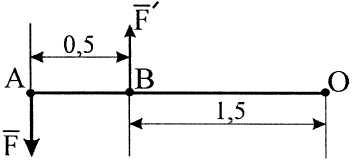ример 14. Силы (F, F'), равные 30Н, образуют пару с плечом 0,5м. Найти момент пары сил относительно точки О, если ОВ =1,5м (рис. 4).

Р

Рисунок 4

ешение. Найдем модуль момента пары . Знак момента положительный, так как пара стремится повернуться против хода часовой стрелки. Найдем моменты сил и относительно точки О:

, , ,

Момент пары не зависит от положения точки, относительно которой вычисляются моменты сил.

Пример 15. О

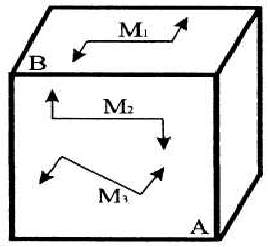
пределить модуль момента эквивалентной пары сил, если известны пары сил с моментами: , , . Направление моментов показано на рис. 6.

Р

Рисунок 6

Рисунок 6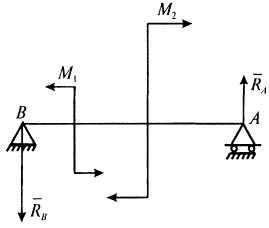

ешение. В плоскости А действуют два момента, направленных противоположно: . Сложим моменты, действующие в перпендикулярных плоскостях А и В: .

Ответ. Момент эквивалентной пары равен

Пример 16. Найти результирующую пару, которая уравновесила бы две пары сил с моментами, , , приложенные к балке АВ длиной 2м (рис. 7).

Р

Рисунок 7

Рисунок 7

ешение. Используя принцип освобождаемости от связей, заменяем действие опор на балку реакциями и . Вектор силы перпендикулярен опорной поверхности. Вектор силы должен быть параллелен , так как они должны образовать эквивалентную результирующую пару. Исходя из условия равновесия пар сил, запишем: , . Так как дана длина балки, то можно найти силы, образующие результирующую пару:

.

Ответ. . Величина результирующего момента получилась с плюсом. Это означает, что направление реакций в точках А и В выбрано правильно.

ТЕМА 5

П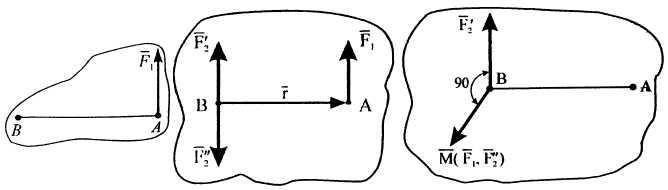ример 17. Перенести силу , приложенную в точке А, в новый центр на расстоянии 0,2 м от точки А (рис. 2, а).

Р

Рисунок 2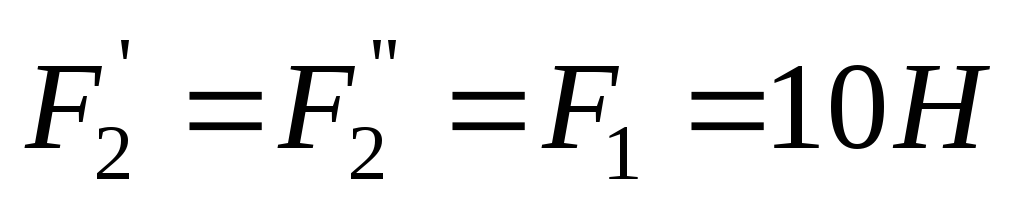

ешение. Согласно теореме о приведении силы к заданному центру, приложим в точке В силу .

В точке В приложим пару сил, которая образована силами и определим векторный момент присоединенной пары (рис. 2,б):

.

Модуль момента пары равен:

, , .

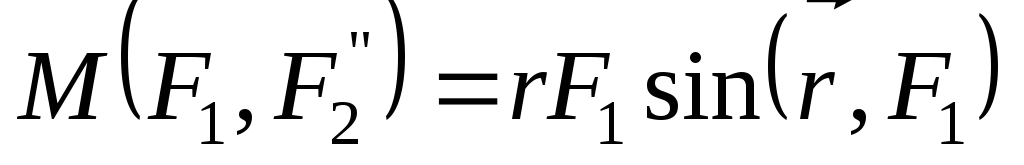Векторный момент перпендикулярен плоскости векторов и и направлен в сторону читателя в соответствии с правилом знаков (рис. 2, в).

П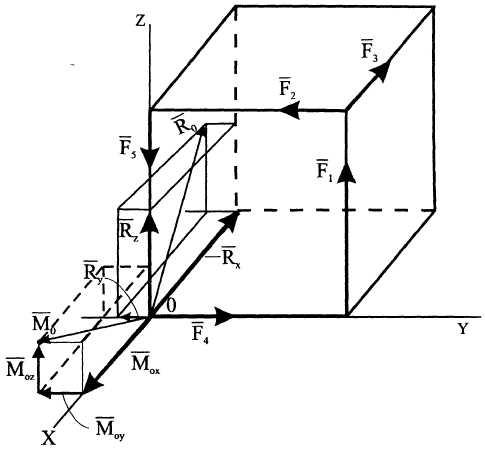ример 18. Найти главный вектор и главный момент системы сил, приложенных к кубу. Известно, что , , , , . Ребро куба а = 0,5м (рис. 4).

Р

Рисунок 4

Рисунок 4

ешение. — модуль главного вектора. Находим проекции главного вектора на оси координат: , , , .

Модуль главного момента . Находим проекции главного момента на оси координат: , ,

, .

Углы, образованные главным вектором и главным моментом с осями координат:

, , ,

, , .

Ответ. , .

П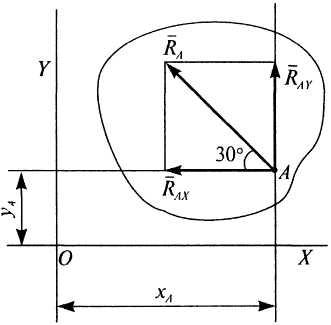ример 19. Система сил приведена к равнодействующей. Определить момент равнодействующей =100Н относительно начала координат, если =0,15м, =0,12м (рис. 7).

Решение. Применим теорему Вариньона . Находим проекции равнодействующей на оси координат:

Рисунок 7

, .

Находим моменты проекций равнодействующей относительно точки О:

, , .

Ответ.

П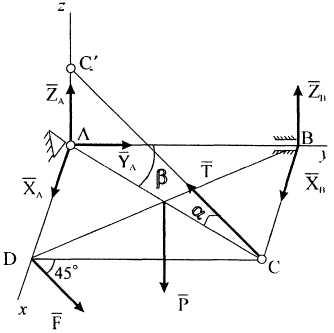ример 20. Прямоугольная однородная плита весом Р удерживается в горизонтальном положении тросом СО. Определить реакции связей, если Р=100Н, F=40Н, =30°, =60°, (рис. 8).

Р

Рисунок 8

Рисунок 8

ешение. Используя принцип освобождаемости от связей, заменим действие связей реакциями, приложенными к плите. В точке А (сферический шарнир) будут три составляющие: Х_А, Y_A, Z_A. В точке В — две составляющие: X_B, Z_B . Реакцию нити Т направим по линии .

Для уравновешенной произвольной пространственной системы сил составим шесть уравнений равновесия:

1. 

2. 

3. 

4. 

5. 

6. 

Находим из 6: ,

из 5: ,

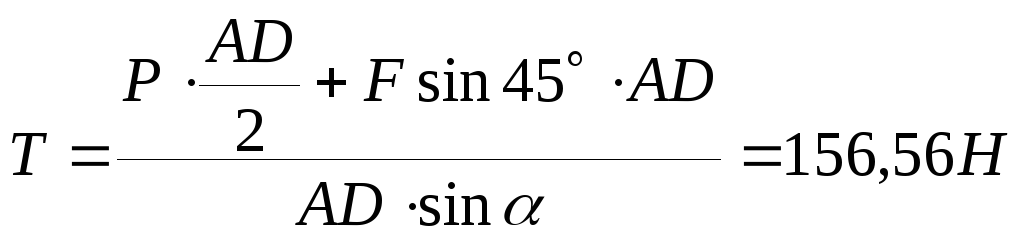из 4: ,

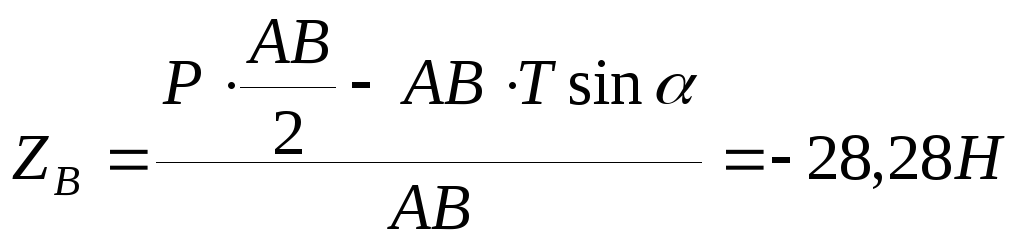из 1: ,

из 2: ,

из 3: .

Ответ. , , , , , .

Минус показывает, что направление противоположно направлению, показанному на рис 8.

Пример 21. Квадратная однородная плита весом Р находится в равновесии. Определить реакции связей, если P=100Н; F=20H (рис. 9).

Р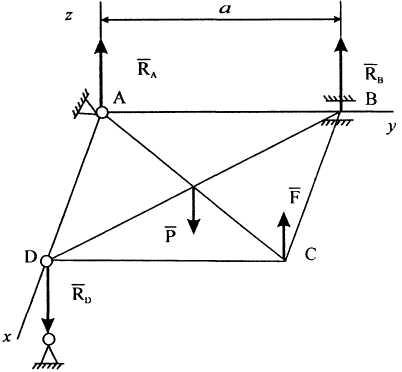ешение. Рассмотрим равновесие плиты под действием системы параллельных сил , и реакций связей , , . Составим три уравнения равновесия:

1. ,

2. ,

3. .

Находим из 2: ,

и

Рисунок 9

з 3: ,

из 1: .

Ответ. , , . Минус показывает, что реакция связей направлена противоположно направлению, показанному на рис. 9.

П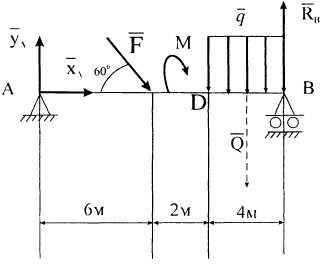ример 22. Определить реакции опор, если F=10кН, q=2кН/м, М=3кНм (рис. 10).

Р

Рисунок 10

ешение. Рассмотрим равновесие балки АВ под действием силы F, момента М, равномерно распределенной нагрузки и реакций связей , , . Составим три уравнения равновесия по первой форме. Равномерно распределенную нагрузку заменим равнодействующей Q=4q=8кН, которая приложена в середине участка BD:

1. , 2. ,

3. .

Находим из 1: , из 3: ,

из 2: .

О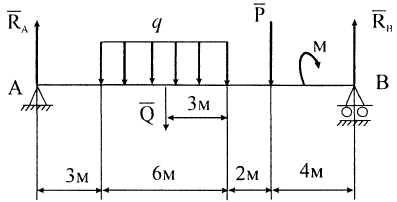твет. X_A = -5 kH, Y_a = 5,41 kH, R_B = 11,25 kH. Минус показывает, что направление Х_А противоположно направлению, показанному на рис 10.

Пример 23. Определить реакции опор, если Р=6кН, q=1кН/м, М=4 кНм (рис 11).

Р

Рисунок 11

Рисунок 11

ешение. Рассмотрим равновесие балки АВ под действием силы , момента , равномерно распределенной нагрузки интенсивности q и реакций связей , . Составим два уравнения равновесия по первой форме. Равномерно распределенную нагрузку заменим равнодействующей , которая приложена к середине нагруженного участка:

1. , 2. .

Находим из 2: , из 1: .

Ответ. , .