
Раздел 1. Статика (примеры).
Тема 1.
Пример 1. Груз, подвешенный на пружине, находится в равновесии. Сила тяжести, обусловленная притяжением Земли, является внешней силой. Силы упругости, возникающие при растяжении пружины, будут внутренними силами
П Рисунок 5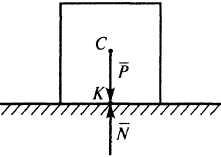 ример
2. Т
ример
2. Т
 ело
находится на гладкой горизонтальной
поверхности и давит на эту поверхность
с силой
ело
находится на гладкой горизонтальной
поверхности и давит на эту поверхность
с силой
![]() .
В свою очередь
поверхность действует
на тело с силой
.
В свою очередь
поверхность действует
на тело с силой
![]() .
Сила
.
Сила
![]() — сила действия, а сила
— сила действия, а сила
![]() — противодействия.
Эти силы равны по модулю и противоположно
направлены, но приложены
к различным телам (рис. 5).
— противодействия.
Эти силы равны по модулю и противоположно
направлены, но приложены
к различным телам (рис. 5).
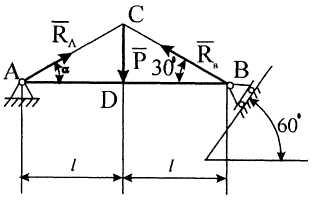
Пример
3. На
середину балки
![]() действует сила
действует сила
![]() (рис. 15). В точке
(рис. 15). В точке
![]() балка имеет шарнирно-неподвижную опору,
а в точке
балка имеет шарнирно-неподвижную опору,
а в точке
![]() — шарнирно-подвижную. Определить линию
действия реакции в точке
— шарнирно-подвижную. Определить линию
действия реакции в точке
![]() .
.
Р
Рисунок
15![]() шарнирно-неподвижной
опоры перпендикулярна
опорной поверхности и пересекается с
линией действия силы
шарнирно-неподвижной
опоры перпендикулярна
опорной поверхности и пересекается с
линией действия силы
![]() в точке
в точке
![]() .
По теореме о трех
непараллельных силах
реакция опоры
.
По теореме о трех
непараллельных силах
реакция опоры
![]() должна пройти
через эту точку:
должна пройти
через эту точку:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ.
Реакция
![]() образует
угол 30° с осью балки АВ.
образует
угол 30° с осью балки АВ.
Тема 2.
Пример
4. Л
Рисунок
1![]() называют системой сходящихся сил (рис.
1).
называют системой сходящихся сил (рис.
1).
Пример
5. И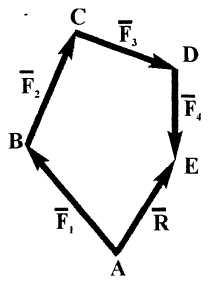 спользуя
условие примера 4, найти равнодействующую
этой системы сил, построив векторный
многоугольник сил.
спользуя
условие примера 4, найти равнодействующую
этой системы сил, построив векторный
многоугольник сил.
Р
Рисунок
2![]() (рис. 2) проводим линию, параллельную
вектору силы
(рис. 2) проводим линию, параллельную
вектору силы
![]() ,
и откладываем отрезок
,
и откладываем отрезок
![]() ,
равный в масштабе модулю этой силы. Из
точки
,
равный в масштабе модулю этой силы. Из
точки
![]() проводим отрезок
проводим отрезок
![]() ,
параллельный вектору силы
,
параллельный вектору силы
![]() и равный в масштабе модулю этой силы.
Из точки
и равный в масштабе модулю этой силы.
Из точки
![]() проводим отрезок
проводим отрезок
![]() ,
параллельный вектору силы
,
параллельный вектору силы
![]() и равный в масштабе модулю этой силы.
Из точки
и равный в масштабе модулю этой силы.
Из точки
![]() проводим отрезок
проводим отрезок
![]() ,
параллельный вектору силы
,
параллельный вектору силы
![]() и равный в масштабе модулю этой силы.
Отрезок
и равный в масштабе модулю этой силы.
Отрезок
![]() ,
который соединяет
начало вектора
,
который соединяет
начало вектора
![]() с концом вектора
с концом вектора
![]() ,
будет равнодействующей этой системы
сходящихся сил. Величина
равнодействующей равна в масштабе
отрезку
,
будет равнодействующей этой системы
сходящихся сил. Величина
равнодействующей равна в масштабе
отрезку
![]() .
.
Ответ.
Равнодействующая заданной системы
сходящихся сил проходит
через точку схода сил
![]() ,
направлена
от точки
,
направлена
от точки
![]() к
точке
к
точке
![]() .
Величина
равнодействующей равна в масштабе
отрезку
.
Величина
равнодействующей равна в масштабе
отрезку
![]() .
.
П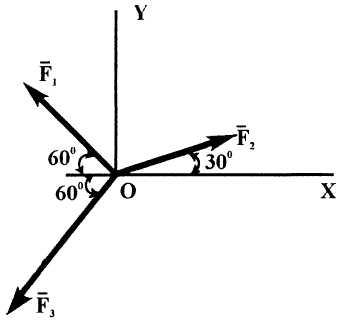
 ример
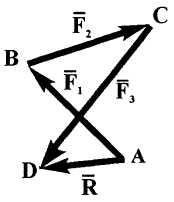
6. В
точке
ример
6. В
точке
![]() приложены силы
приложены силы
![]() =26Н,
=26Н,
![]() =26Н,
=26Н,
![]() =44Н.
Определить величину и направление
равнодействующей (рис.3, а).
=44Н.
Определить величину и направление
равнодействующей (рис.3, а).
Р
Рисунок
3(а, б)![]() ,
прикладываем ее в точке А,
,
прикладываем ее в точке А,
![]() проводим с конца
вектора
проводим с конца
вектора
![]() ,
,
![]() проводим с конца вектора
проводим с конца вектора
![]() .
Конец вектора
.
Конец вектора
![]() соединяем с точкой
А. На
рис.3, б
соединяем с точкой
А. На
рис.3, б
![]() =АВ,
=АВ,
![]() =ВС,
=ВС,
![]() =CD,
=CD,
![]() =AD.
=AD.
б) Аналитический метод
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
Пример
7. Т
Рисунок
4(а, б)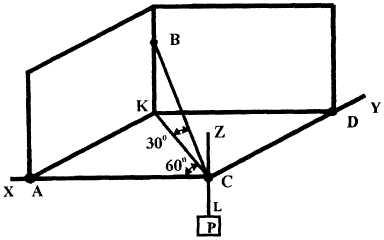
 ри
невесомых стержня соединены в точке
ри
невесомых стержня соединены в точке
![]() шарниром, к которому
нитью прикреплен груз Р=100Н.
В положении, когда плоскость ACDK
горизонтальна,
ACK=60°,
BCK=30°,
найти усилия в стержнях
шарниром, к которому
нитью прикреплен груз Р=100Н.
В положении, когда плоскость ACDK
горизонтальна,
ACK=60°,
BCK=30°,
найти усилия в стержнях
![]() ,
,
![]() ,
,
![]() .
Направление осей
координат показано на
рис.4, а.
.
Направление осей
координат показано на
рис.4, а.
Решение.
На
основании принципа освобождаемости от
связей заменяем
действие стержней
![]() ,
,
![]() ,
,
![]() и
нити
и
нити
![]() на
шарнир
на
шарнир
![]() реакциями:
Sас,
Scd,
Sвс,
Т,
которые
направляем от шарнира
(рис.4, б), считая, что Т=Р.
Найдем
проекции всех сил на соответствующие
оси и запишем уравнения равновесия (7).
Уравнения равновесия
принимают вид
реакциями:
Sас,
Scd,
Sвс,
Т,
которые
направляем от шарнира
(рис.4, б), считая, что Т=Р.
Найдем
проекции всех сил на соответствующие
оси и запишем уравнения равновесия (7).
Уравнения равновесия
принимают вид
Находим
из 3:
![]() из
2:
из
2:
![]()
из
1:
![]()
Ответ. SBC = 200 H, SCD = -150 H, SAC = -87 H. Минус означает, что стержни АС и CD сжаты, а не растянуты, как предполагалось вначале.
П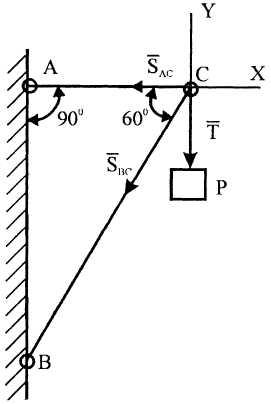 ример
8. Два
невесомых стержня, соединенные в точке
С
шарниром,
удерживают
груз весом Р=50Н,
который нитью прикреплен к шарниру
С.
Найти усилия в стержнях АС
и ВС,
если CB=
60°.
ример
8. Два
невесомых стержня, соединенные в точке
С
шарниром,
удерживают
груз весом Р=50Н,
который нитью прикреплен к шарниру
С.
Найти усилия в стержнях АС
и ВС,
если CB=
60°.
Р
Рисунок
5
Находим
из 2:
![]() из
1:
из
1:
![]()
Ответ. SBC = -57,74 Н, SAC = 28,87 Н. Отрицательное значение указывает, что стержень ВС сжат, а не растянут, как предполагалось.
