8. Исследование функций при помощи производной. ( Возрастание, убывание, минимумы, максимумы, уравнение касательной к графику функции)

Возрастание и убывание функции

Для того, чтобы дифференцируемая на интервале ( a ;  b ) функция f была неубывающей на этом интервале, необходимо и достаточно, чтобы выполнялось условие для любого Аналогичным образом определяется необходимое и достаточное условие невозрастания функции f :

Экстремумы. Напомним, что в точке x ₀ функция достигает экстремума, если для любых x из некоторой окрестности точки x ₀ выполняется неравенство f  ( x ) ≤  f  ( x ₀ ) (минимум) или f  ( x ) ≥  f  ( x ₀ ) (максимум).

Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю.

Точки, в которых производная функции равна нулю, называются стационарными точками функции. Точки, в которых производная функции равна нулю или не существует, называются критическими точками. Таким образом, все экстремумы являются критическими точками

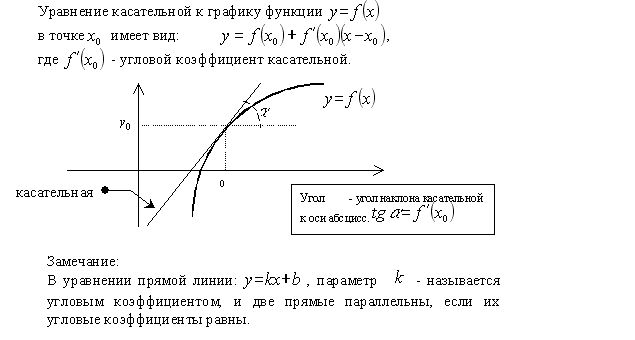
Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.Производной функции f(x) в точке x₀ называется предел отношения приращения функции в этой точке f=f(x0+x)−f(x0) к приращению аргумента x при x0: f(x0)=limx0xf(x0+x)−f(x0).

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.