1. Определение матрицы. Сложение матриц и умножение матрицы на число. Матричное умножение. Соотношения между размерами складываемых и перемножаемых матриц. Преобразование вектора при помощи матрицы. Ма́трица — математический объект, записываемый в виде прямоугольной (двумерной) таблицы чисел и допускающий алгебраические операции между ним и другими подобными объектами. У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен b_ij = λa_ij Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен c_ij = a_ij + b_ij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой c_ij = a_ij - b_ij

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть A + Θ = A . Все элементы нулевой матрицы равны нулю.Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть .

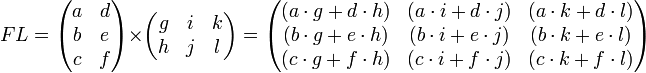
Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Сложение и вычитание допускается только для матриц одинакового размера, а при умножении, в первом множителе должно быть столько же столбцов, сколько строк во втором. Минором определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент.

2. Алгебраические дополнения и их свойства. Обратная матрица. Определение и метод нахождения.

Алгебраическим дополнением данного элемента называется его минор, умноженный на ( - 1)^k, где k - сумма номеров строки и столбца, содержащих данный элемент. Матрица B называется обратной по отношению к матрице A, если произведение AB равно единичной матрице: AB = E. обозначается А^-1. Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.Найти обратную матрицу. Вычисляем определитель матрицы A:

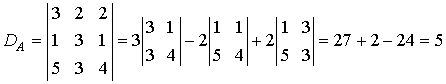
   Находим алгебраические дополнения элементов этого определителя:

,   ,    ,   ,    ,   ,   

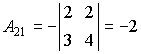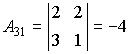
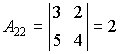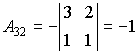
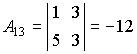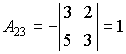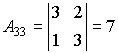
   Следовательно, (выполняется переместительный закон)

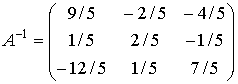
3.Определитель матрицы. Элементарные преобразования, не меняющие определитель. Определитель произведения матриц.

Определитель матрицы является многочленом от элементов квадратной матрицы (т.е. такой, у которой количество строк и столбцов равны). Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Для матрицы порядка 1 детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

В частности, формула вычисления определителя матрицы такова:

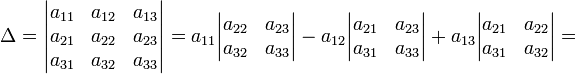
= a₁₁a₂₂a₃₃ − a₁₁a₂₃a₃₂ − a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ − a₁₃a₂₂a₃₁

При транспонировании определитель матрицы не изменяется

существуют преобразования матрицы, не меняющие определителя. Т.е. замена матрицы на другую, но с тем же определителем:

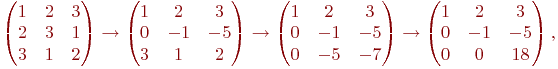
и мы пришли к треугольному виду. При этом мы применяли только преобразования 1-го типа, не меняющие определитель. Следовательно, .

4. Ранг матрицы. Теорема Кронекера-Капелли о числе решений системы линейных уравнений.

Рангом матрицы A называется наибольший порядок отлчиных от нуля миноров этой матрицы. Если все элементы матрицы равны нулю,то ранг этой матрицы принимают равным нулю.    Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.    Ранг матрицы A будем обозначать через r (A). Если r (A) = r( B), то матрицы A и B называются эквивалентными.

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A иA совпадают, т.е. r(A) = r(A) = r.

Для множества М решений системы (5.1) имеются три возможности:

1) M =  (в этом случае система несовместна);

2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);

3) M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.

Система имеет единственное решение только в том случае, когда r(A) = n. При этом число уравнений - не меньше числа неизвестных (mn); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.

Исследовать систему уравнений и решить ее, если она совместна:

5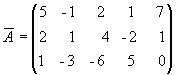x₁ -   x₂ + 2x₃ +  x₄  = 7,

2x₁ +  x₂ + 4x₃ -  2x₄ = 1,

x₁ - 3x₂ -  6x₃ + 5x₄ = 0.

Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу  = 7  0; содержащие его миноры третьего порядка равны нулю:

 

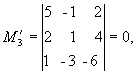
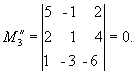
С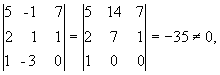ледовательно, ранг основной матрицы системы равен 2, т.е. r(A) = 2. Для вычисления ранга расширенной матрицы A рассмотрим окаймляющий минор

значит, ранг расширенной матрицы r(A) = 3. Поскольку r(A)  r(A), то система несовместна.