Единицы измерений

Давление измеряется в (Паскаль) = = = =.

Интенсивность звука измеряется в . Уровень интенсивности звука измеряется в децибелах или в Белах ():

;

,

где – пороговая интенсивность.

Уровень акустического давления определяется по и акустическому сопротивлению . Тогда пороговое давление

;

.

Например, давлению соответствует уровень давления .

В таблицах 3.2 и 3.3 представлены отношения интенсивностей и давлений и соответствующие им разности уровней.

Таблица 3.2

;	, дБ	, дБ	;	, дБ	, дБ
2	3	6	10	10	20
3,16	5	10	100	20	40
4	6	12

Таблица 3.3

	1	1,26	2	4	5	10	102	103	104	106	1010
	1	1,16	1,41	2	2,24	3,16	10	31,6	102	103	105
, дБ	0	1	3	6	7	10	20	30	40	60	100

Частотный состав акустических колебаний определяется спектром. Частота колебаний (число колебаний в секунду) измеряется в Герцах . Диапазон частот колебаний, в котором частота изменяется в два раза, то есть

,

называется октавой. Третья часть октавы (в логарифмическом масштабе частот) определяет третьоктавную полосу спектра. Соотношения для граничных частот определяются следующим образом:

;

.

Средняя частота ,

(6% полоса спектра – 1/4 от третьоктавного).

Сложение уровней

При суммировании уровней звука складываются мощности или квадраты давлений , поочередно, от большего к меньшему.

Например, при суммировании двух уровней звука , где , имеем

;

;

,

где .

При , , .

Связь спектральных и третьоктавных уровней:

.

Так как ,

то ;

.

;

.

Закономерности движения акустических волн. Волновое уравнение. Движение в канале постоянной площади

В канале распространяется плоская волна, интенсивность которой зависит от мощности источника и площади сечения канала. Эта интенсивность не зависит от расстояния, если пренебречь потерями на вязкость, турбулентность и другими диссипативными потерями.

Движение волн определяется решениями волнового уравнения

, .

Решение волнового уравнения состоит из двух членов, описывающих распространение волн в положительном и отрицательном направлениях оси . При синусоидальной зависимости от времени давление и скорость колебаний частиц газа в плоской волне описываются выражениями

;

,

где ; – волновое число.

Амплитуда смещения и амплитуда скорости частиц газа в волне связаны соотношением . Давление и скорость колебаний в плоской волне совпадают по фазе, поэтому акустическое сопротивление – действительная величина, равная активному сопротивлению .

Интенсивность плоской волны

.

Сферическая волна

Волновое уравнение в сферических координатах

.

Частное решение (для распространяющейся из центра волны)

.

Скорость колебаний

;

,

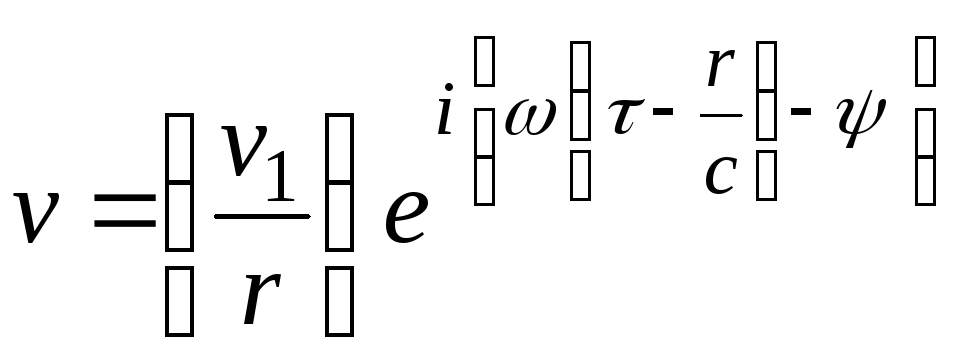где – амплитуда скорости на расстоянии единицы длины от центра:

,

где – сдвиг фаз между давлением и скоростью колебаний,

,

где – длина волны.

На средних частотах на расстоянии, большем , можно пренебречь сдвигом фаз.

Распространение волн от источника в центре сферы

Полная мощность зависит от источника и, в случае пренебрежения потерями, не изменяется с расстоянием от источника.

Интенсивность звука с расстоянием уменьшается из-за роста поверхности сферической волны по квадратичной зависимости от радиуса сферы

.

Звуковое давление уменьшается обратно пропорционально радиусу сферы

,

где , – интенсивность и давление на расстоянии единицы длины () от центра.

Цилиндрическая волна

Цилиндрическая волна возникает от источников, расположенных цепочкой по длине прямой. Интенсивность звука убывает обратно пропорционально расстоянию от оси источников

,

а звуковое давление, изменяющееся по закону

.