РЯДЫ

Аннотация.

Ряды, представляющие собою бесконечные суммы элементов числовых и функциональных последовательностей, являются эффективным математическим инструментом, применяемым для вычислений и исследований, как в различных разделах самой математики, так и во многих ее приложениях.

Тема 2.1. Числовые ряды 1. Понятие числового ряда. Основные определения.

2.Свойства сходящихся рядов.

3. Необходимые условия сходимости рядов. 4. Ряды с неотрицательными членами. Признаки сходимости рядов с неотрицательными членами: можарантный признак, признак Даламбера, признак Коши, интегральный признак.

Конспект лекции

1. Понятие числового ряда. Основные определения.

Пусть дана числовая последователь­ность

Выражение вида

(1)

называется числовым рядом или просто рядом.

Числа называются членами ряда, член с про­извольным номером — общим членом ряда.

Суммы конечного числа членов ряда

называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм

(2)

Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу , которое в этом случае называется суммой ряда (1). Символически это запи­сывается так:

или .

Если же последовательность частичных сумм (2) расходится, то ряд (1) называется расходящимся.

Пример 1. Покажем, что ряд

сходится. Возьмем сумму первых членов ряда

.

Слагаемые этой суммы могут быть представлены в виде

.

Поэтому

.

Отсюда следует, что предел последовательности частичных сумм данного ряда равен единице:

.

Таким образом, ряд сходится, и его сумма равна 1.

Пример 2. Установим, сходится или расходится ряд

.

Последовательность его частичных сумм имеет вид и, значит, не сходится ни к какому пределу, поэтому данный ряд расходится.

Пример 3. Рассмотрим ряд, составленный из элементов геомет­рической прогрессии

. (3)

Частичная сумма этого ряда при имеет вид

.

Отсюда:

1) если , то , т. е. ряд сходится и его сумма . Например, при имеем: ;

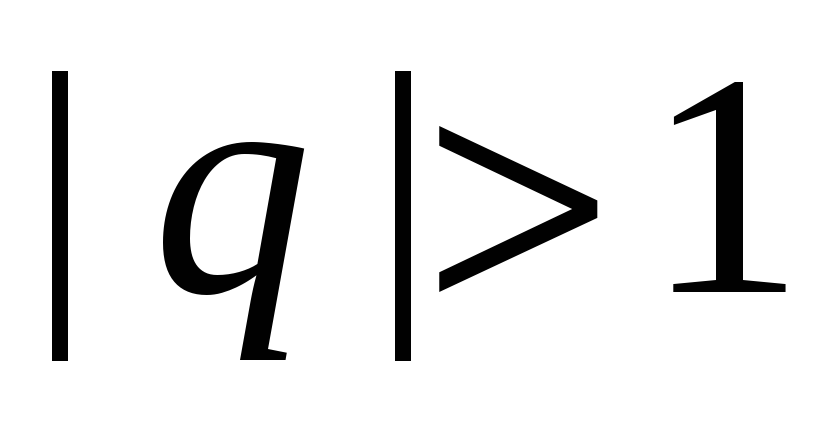2. если , то 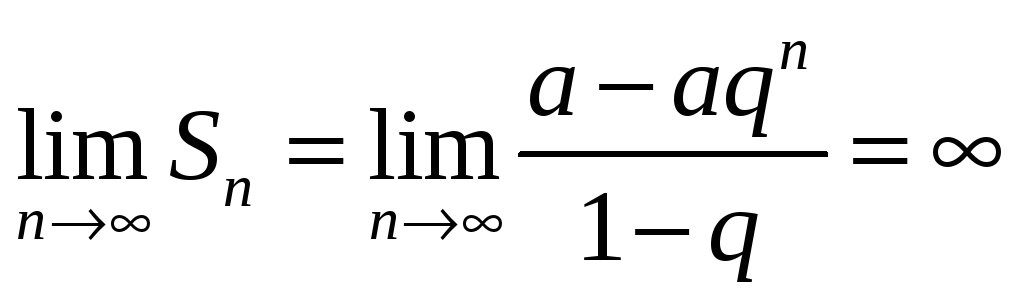, т. е. ряд расхо­дится;

3. при 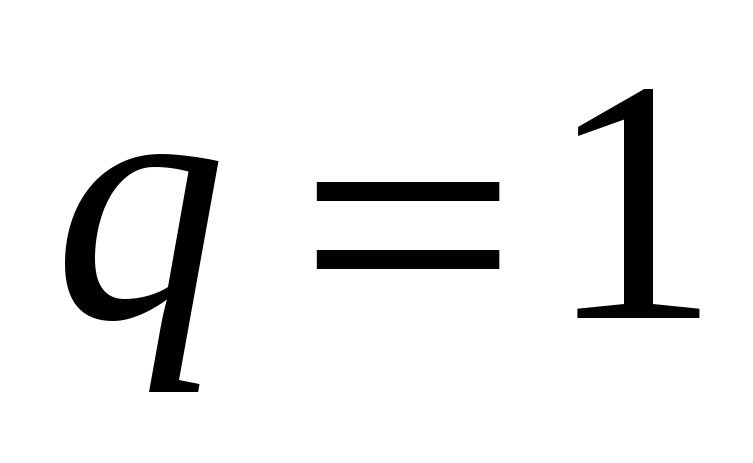ряд (3) принимает вид

В этом случае , т. е. ряд расходится;

4) при ряд (3) принимает вид Для него , т. е. при четном и при нечетном. Следовательно, не существует и ряд расходится.

Таким образом, ряд (3) является сходящимся при и расходящимся при .

2. Свойства сходящихся рядов.

Теорема 1. Если схо­дится ряд

, (4)

то сходится и ряд

, (5)

и обратно, если сходится ряд (5), то сходится и ряд (4).

Другими словами, на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.

Доказательство. Пусть ряд (4) сходится и имеет сумму , т. е. . Обозначим через сумму отброшенных членов ряда (4), а через сумму первых членов ряда (5). Тогда

, (6)

где — некоторое число, не зависящее от . Из равенства (6) следует

,

т. е. последовательность частичных сумм ряда (5) имеет предел, что означает сходимость ряда (5).

Пусть теперь ряд (5) сходится и имеет сумму , т. е. . Тогда из (6) следует

,

что означает сходимость ряда (4). Теорема доказана.

Над сходящимися рядами можно выполнять обычные арифмети­ческие действия.

Т е о р е м а 2. Если ряд сходится и его сумма равна , то и ряд , где — некоторое число, также сходится, и его сумма равна .

Доказательство. Пусть — частичная сумма ряда , а — частичная сумма

ряда . Тогда

.

Отсюда, переходя к пределу при , получаем

,

т. е. последовательность частичных сумм ряда сходится к . Следовательно, . Теорема доказана.

Теорема 3. Если ряды и сходятся и их суммы соответственно

равны и , то и ряд сходится и его сумма равна .

Доказательство. Пусть и — частичные суммы рядов и , а —

частичная сумма ряда . Тогда

.

Отсюда, переходя к пределу при , получаем

,

т. е. последовательность частичных сумм ряда сходится к . Следовательно, . Теорема доказана.

Таким образом, установлено, что сходящиеся ряды можно умно­жать на число, почленно складывать и вычитать так же, как и ко­нечные суммы.