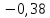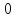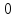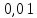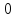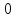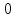4.2.Расчет прицельных поправок воздушной стрельбы

Прицельные поправки определяются из формул скалярных уравнений задачи прицеливания.

Представим скалярное уравнение на ось y_D в следующем виде:

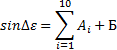
(4.6)

где -параметр в формуле (4.6); - слагаемое, учитывающее влияние на прицельную поправку i –ого фактора.

После преобразования формулы выражения для слагаемых принимают вид (вычисления с точностью до второго знака после запятой)

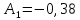
(4.7)

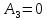
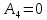
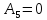
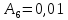
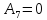
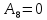
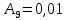
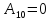
где определяется выражением .

(4.8)

Решим проекцию скалярного уравнения на ось z_D относительно , представив его в следующем виде:

(4.9)

где _, - делитель в формуле (4.9) и слагаемое, учитывающее влияние на прицельную поправку фактора.

После преобразования формулы выражения для слагаемых будут иметь вид

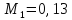
(4.10)

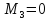
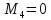
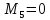
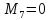
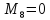
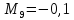
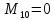
Из полученных формул видно, что в процессе приближений уточняются только слагаемые Б и N, а суммы и неизменны.

Вычисление прицельных поправок:

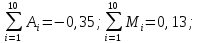
Вычисляем отдельно слагаемые и их сумму .

При вычислении параметра N, входящего в формулу (4.9), делаем первое

приближение _.

Тогда

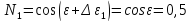
Определяем первое приближение угловой поправки воздушной стрельбы в виде

Находим первое приближение величины Б, входящей в формулу (4.6),

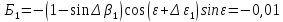
_{Вычисляем} второе приближение угловой поправки

Находим второе приближение параметра N

_{Вычисляем} второе приближение прицельной поправки

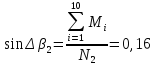
Находим второе приближение величины Б

_{Вычисляем} третье приближение угловой поправки

Находим третье приближение параметра N

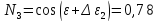
_{Вычисляем} второе приближение прицельной поправки

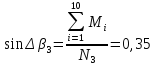
Отсюда находим прицельные поправки:

Прицельные поправки воздушной стрельбы, бортовой угол и угол места визирной линии используются для определения потребных значений бортового угла и угла места оружия

Расчет прицельных поправок заканчивается составлением и анализом таблицы 4.1.

Таблица 4.1.

Итоговая таблица

	Источник поправки
			Значение		Значение
1.	Движение цели				0,16
2.					0
3.	Угол атаки		0		0
4.	Угол скольжения		0		0
5.	Ускорение цели				0
6.					0,02
7.					0
8.					0
9.	Бортовой эффект				0
10.	Понижение				0
11.	Согласующее слагаемое		0	-	-

Рассмотрим и проанализируем данную таблицу. Заметим, что в основном на величину прицельных поправок влияет движение цели. Незначительно влияет бортовой эффект и положение визирной системы относительно оружия.