3. Расчет дополнительных параметров условий стрельбы
Дополнительными
параметрами условий стрельбы являются
скорость сближения с целью
и проекции абсолютной угловой скорости
визирной линии
.
Формулы для вычисления дополнительных
параметров могут быть получены из
уравнения для вектора скорости цели в
случае ее определения синхронным
способом.
.
(3.1)
Переведя все векторы в систему координат “D”, получим следующие зависимости для определения искомых параметров
(3.6)
,
(3.7)
,
.
(3.8)
Для
определения проекций вектора
поступаем следующим образом. Введем
систему координат
,
связанную с вектором воздушной скорости
цели
.
Система координат ''
''
получается путем поворота базовой
системы координат на углы
.
Тогда проекции вектора
на оси системы координат “D”
могут быт определены путем перемножения
следующих матриц преобразования
координат
.
Тогда
(3.10)
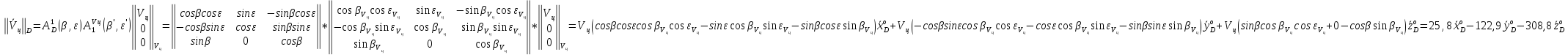
Проекции вектора на оси системы ''D'' могут быть определены из произведения следующих матриц
,
(3.11)
где
-
матрица перехода от системы ''
'' к системе
''1'', определяемая углами атаки и
скольжения.
Так как для расчета дополнительных параметров можно сделать допущения (из-за малости углов атаки и скольжения), то
.
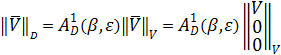(3.12)
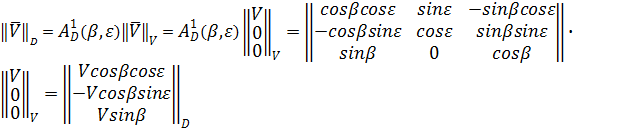
(3.13)
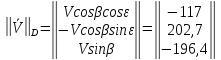
Тогда получим:
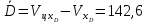
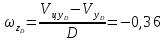
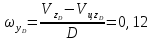
В
расчетных формулах, определяющих
параметры Δβ и Δε и Dу
, также имеются проекции ускорения
цели
на оси лучевой системы координат “D”.
Эти проекции в прицельной системе должны
вычисляться в зависимости от измеряемых
и вычисляемых параметров
.
В
курсовой работе проекции ускорений
вычисляются в зависимости от заданных
параметров условий стрельбы, точнее, в
зависимости от заданной величины
ускорения цели и ориентации вектора
в системе “D”.
Для цели №1 ускорение равно нулю.
4. Расчет и анализ прицельных поправок
Расчет
прицельных поправок выполняется в два
этапа. На первом этапе выполняется
расчет методом последовательных
приближений упрежденной дальности
, времени полета
снаряда
и понижения
, которые не
зависят от поправок
. На втором
этапе также методом последовательных
приближений выполняется расчет прицельных
поправок воздушной стрельбы
с учетом
вычисленных параметров
,
и
.
4.1. Расчет упрежденной дальности , времени полета и понижения снаряда
Последовательность
расчета параметров
,
и
:
-
Вычисление приведенного баллистического коэффициента производится по формуле
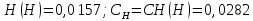
2. Вычисление скорости снаряда относительно воздуха (абсолютной скорости) производится по формуле
3.
Вычисление дополнительных параметров
,
и
.
В качестве первого приближения упрежденной дальности берется дальность до цели
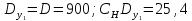
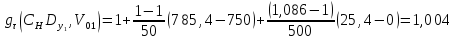
Находим время полета снаряда после первого приближения
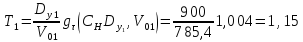
Определяем второе приближение упрежденной дальности при условии малости значений понижения снаряда и бортового эффекта.
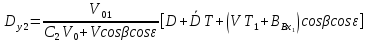
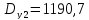
Находим
второе приближение параметра
и второе приближение табличной функции
.
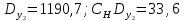
Вычисляем второе приближение времени полета снаряда
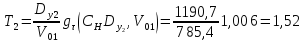
Определим третье приближение упрежденной дальности по указанной выше формуле, но для нового времени
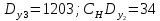
Вычисляем третье приближение времени полета снаряда
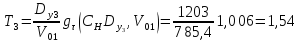
Находим понижение снаряда с учетом полученных выше значений по формуле
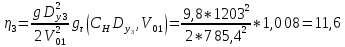
Для расчетов прицельных поправок , определяющих углы между потребным направлением оружия и фактическим направлением на цель, берём значения последнего приближения.