МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Факультет «Робототехнические и интеллектуальные системы»

Кафедра 704 «Информационно-управляющие комплексы»

Кафедра

“Утверждено”

на заседании методсовета ф-та №7

Протокол № _____________________

«_______» _______________________

Г.А.Жуков

Учебное пособие по выполнению

курсовой работы

«Расчет и анализ прицельных поправок воздушной стрельбы»

по дисциплинам:

«Бортовые информационно-управляющие средства оснащения ЛА»

«Информационно-управляющие средства оснащения ЛА»

«Обзорно-прицельные системы»

“Обсуждено”

на заседании кафедры 704

Протокол № ____________

«_______» ______________

Москва 2010 г.

1. Исходные данные курсовой работы

1.1. Характеристики целей

Цель №1 – самолет, выполняющий прямолинейное и равномерное движение ().

Цель №1 (прямолинейное и равномерное движение цели ).

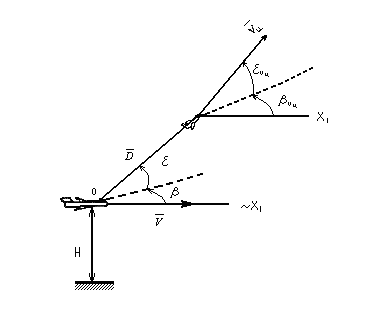
Положение цели в системе координат, связанной с ЛА, определяется дальностью D, бортовым углом цели β и углом места цели ε (при условии совмещения визирной линии с целью). Направление вектора скорости цели №1 определяется углами β_Vц и ε_Vц.

1.2. Начальные условия стрельбы

Начальные условия стрельбы.

Параметры	5
Н, км	30
V , км/час	1100
Vц , км/час	1200
D, м	900
β , град	-140
ε, град	60
βvц, град	70
εvц, град	20
αат, град	6
βск, град	-0020’
γ,υ	0

1.3. Вводимые в прицельную систему величины

Значения величин, вводимых в прицельную систему.

Параметры	2
C, м2/кг	1,8
10-5Cb, с/м	6,5
C2	0,85
V0, м/с	850
Ввx1, м	30
Ввy1, м	3
Ввz1, м	-2

2.1. Векторная схема и векторное уравнение задачи прицеливания

Векторная схема задачи прицеливания при стрельбе из авиационного артиллерийского оружия подвижной пушечной установки (ППУ) с использованием визирной системы оптической прицельной станции бомбардировщика представлена на рис.2.1.

На рис. 2.1. приняты следующие обозначения:

ВП, О, Ц – положения визирно-прицельной подсистемы, снаряда и цели в момент выстрела соответственно;

– положение цели и снаряда через время его полета Т;

- вектор выноса визирной системы относительно оружия;

- вектор понижения снаряда вследствие действия силы тяжести ;

- вектор смещения снаряда вследствие проявления бортового эффекта;

- вектор перемещения цели за время Т полета снаряда;

- векторы дальности до цели, фактической упрежденной дальности и требуемой (расчетной) упрежденной дальности снаряда;

– векторы начальной скорости снаряда относительно самолета, воздушной скорости самолета и скорости снаряда относительно воздуха (абсолютной скорости снаряда);

- вектор дальность полета снаряда по направлению вектора ;

- вектор промаха;

- бортовой угол стрельбы.

Из рисунка следует, что для рассматриваемой прицельной схемы вектор промаха будет определяться из следующего соотношения:

,

(2.1)

где векторы и определяются по формулам:

(2.2)

,

.

Условием задачи прицеливания является минимизация вектора промаха. Положим, что вектор промаха равен нулю, т.е. . Откуда следует, что для решения задачи прицеливания вектор должен быть равен расчетному (требуемому) вектору , т.е.

Так как векторы понижения снаряда и бортового эффекта малы по сравнению с вектором дальности стрельбы , то направление вектора _, как следует из второго уравнения (2.2), определяется единичным вектором _, который выражается зависимостью:

,

где , - векторы, записанные через орты осей систем координат, которые связаны с этими векторами.

Тогда

.

(2.3)

Из (2.3) следует, что направление вектора можно изменять векторами или . Так как оружие подвижно, то изменение направления вектора может быть достигнуто достаточно быстро поворотом вектора оси , направленной по оружию, т.е. путем поворота оружия подвижной пушечной установки.

Таким образом, для попадания снаряда в цель необходимо фактическое конечное положение снаряда (т. ) совместить с требуемым положением (т. ), что согласно формулам (2.2) состоит в реализации равенства

. (2.4)

В силу того, что модули векторов понижения снаряда и бортового эффекта оказываются меньше ошибок измерения дальности, то эти векторы можно не учитывать при определении модуля и тогда вектор дальности стрельбы по модулю приближается к модулю вектора упрежденной дальности. Будем считать, что

(2.5)

.

С учетом уравнений (2.3), (2.4), (2.5) исходное векторное уравнение задачи прицеливания примет вид:

.

(2.6)

Составим систему векторных уравнений и замкнем её ''повекторно''. Замкнуть систему ''повекторно'' значит выразить все векторы полученного векторного уравнения (2.6) через орты осей систем координат, связанных с этими векторами.

,

(2.7)

где - орт системы координат “”, связанной с оружием и ориентированной относительно базовой (самолетной) системы координат бортовым углом и углом места оружия_, которые определяют потребное направление оружия ППУ;

,

(2.8)

где - орт системы координат “”, связанной с вектором воздушной скорости летательного аппарата . Систему координат “” называют скоростной или поточной системой координат. Базовая система координат ориентирована относительно поточной углами скольжения и атаки ;

(2.9)

,

где - орт наземной (стартовой) системы координат “0”. Оси базовой системы координат ориентированы относительно наземной курсовым углом , углом тангажа и углом крена ;

,

(2.10)

где - множитель при векторе бортового эффекта ; - коэффициент бортового эффекта; вектор представлен проекциями на оси базовой системы координат (с учетом малости углов атаки и скольжения можно считать, что ;

(2.11)

,

где - орт лучевой (визирной) системы координат “D” - системы координат, связанной с вектором дальности. Система “D” ориентирована относительно осей базовой бортовым углом и углом места цели .

Вектор выноса визирного устройства относительно оружия в самолетной системе координат может быть записан в виде

.

(2.12)

Для рассматриваемых гипотез движения цели вектор перемещения цели за время полета снаряда T может быть представлен в виде:

где - для цели №5 (самолет противника, атакующий бомбардировщик, выполняет полет по кривой прицеливания) принимается 2-ая гипотеза движения цели a=1, b=1.

Для синхронного способа определения скорости и ускорения цели имеем следующие формулы :

(2.14)

,

(2.15)

.

Решая систему векторных уравнений (2.5) - (2.15) при условии полного замыкания системы, т.е. написания недостающих уравнений для скалярных величин, можно найти потребные бортовой угол и угол места оружия ППУ.