[<Д>Между этими «Д» будут доказательства</Д>]
1. Первообразная. Доказать теоремы о первообразных. Неопределенный интеграл и его свойства. Таблицы неопределенных интегралов, ее вывод.
Функция F(x) называется первообразной
функции f(x)
на интервале (a;b),
если для любого
выполняется равенство
(или
)
Теорема.
Если функция F(x) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задается формулой F(x) + C, где С=const;
<Д>
Функция F(x)+C является первообразной f(x). Действительно,
(F(x)+C)’ = F'(x)=f(x).
Пусть Ф(х) – некоторая другая,
отличная от F(x),
первообразная функции
f(x), т.е.
Ф’(x)=f(x).
Тогда для любого
имеем
Известно, что если производная функции равна нулю на некотором промежутке, то функция постоянна. А это означает, что
Следовательно, Ф(х) = F(x) + C
</Д>
Множество всех первообразных функций F(x) + C для f(x) называется неопределенным интегралом от функции f(x) и обозначается символом
Таким образом, по определению
f(x) – подынтегральная функция
f(x)dx – подынтегральное выражение
x – переменная интегрирования
Свойства:
1.
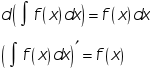
<Д>
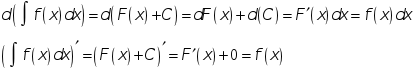
</Д>
2.
<Д>
</Д>
3.
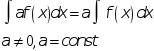
<Д>
</Д>
4.
<Д>
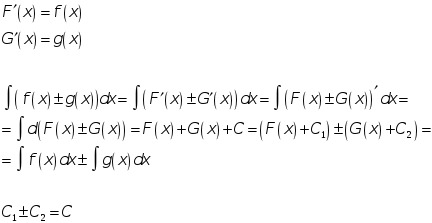
</Д>
5. (Инвариантность формы интегрирования)
Если
,
то и
,
где
<Д>
Пусть x – независимая
переменная, f(x) – непрерывная
функция и F(x) – ее
первообразная. Тогда
.
Положим теперь
где
- непрерывно-дифференцируемая функция.
В силу инвариантности формы первого
дифференциала
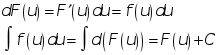
</Д>
Таблица основных интегралов:
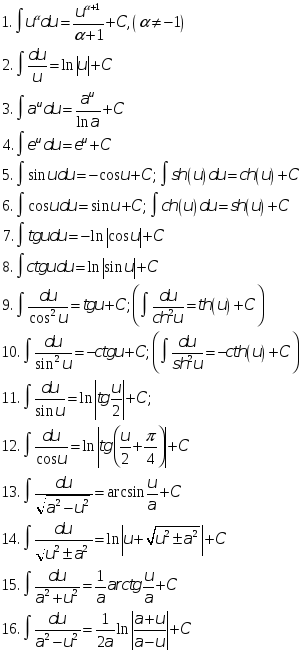
2. Интегрирование подстановкой и по частям. Примеры. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование тригонометрических и иррациональных функций.
Подведение под знак дифференциала:
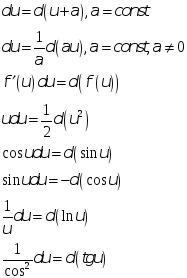
Метод интегрирования подстановкой.
Пусть требуется вычислить интеграл
.
Сделаем подстановку
,
где
-
функция, имеющая непрерывную производную.
Тогда
и
на основании свойства инвариантности
формулы интегрирования
Метод интегрирования по частям
Пусть u=u(x) и v=v(x) – функции, имеющие непрерывные производные. Тогда d(uv)=udv+vdu. Интегрируя это равенство получим
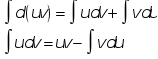
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям
1. Удобно использовать подстановку u = P(x), dv – все остальное:
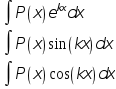
2. P(x)dx = dv, u – все остальное:
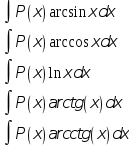
3. u=eax
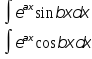
Квадратичные иррациональности.
Интегралы типа
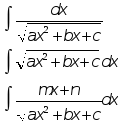
называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом:
под радикалом выделить полный квадрат
и сделать подстановку
.
При этом первые два интеграла приводятся
к табличным, а третий – к сумме двух
табличных интегралов.
Интегрирование тригонометрических и иррациональных функций.
Универсальная тригонометрическая
подстановка. Вычисление интегралов
вида
сводится
к вычислению интегралов от рациональной
функции подстановкой
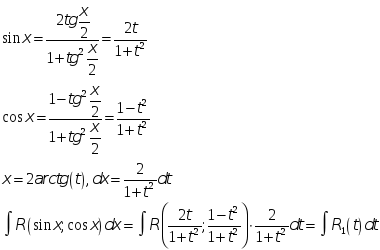
Дробно линейная подстановка
где a,b,c,d – действительные
числа,
-
натуральные числа, сводятся к интегралам
от рациональной функции путем подстановки
,
где k – наименьшее общее
кратное знаменателя дробей
.
Тригонометрическая подстановка
Интегралы типа
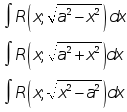
приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок соответственно:
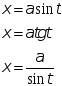
Интегралы типы
Выделив под радикалом полный квадрат
и сделав подстановку
,
интегралы указанного типа приводятся
к интегралам
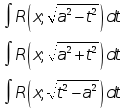
[Из лекций:]
1) Подстановка Эйлера.
Если a>0
Пусть для определенности перед
знак +. Возведем все в квадрат
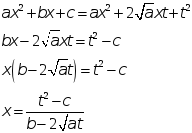
что приведет исходный интеграл к интегралу от рациональной функции.
2) Если с > 0 тогда
Для определенности возьмем перед
знак
+.
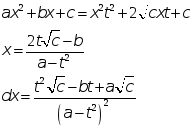
3) Пусть
-действительные
корни
