
- •Постановка задач
- •Математическое описание методов
- •2.1. Метод хорд
- •2.2 Решение систем линейных уравнений методом Зейделя
- •2.3. Метод Рунге-Кутта
- •Блок-схема модуля hord1 (процедура hord)
- •3.3 Блок-схема модуля roonge1 (процедура roonge)
- •Описание стандартных функций
- •5 Описание нестандартных функций
- •6 Описание интерфейса
- •7 Численные примеры
АННОТАЦИЯ
Курсовая работа по информатике на тему объектно-ориентированное программирование на примере численных методов выполнена по заданию №16: приближенное вычисление алгебраических и трансцендентных уравнений методом хорд, решение системы линейных уравнений методом Зейделя, решения дифференциальных уравнений методом Рунге-Кутта; выполнена студентом группы СРС-11 Самойловым Д.О., под руководством Артёмовой С.В.
Содержит 27 листов основного текста, 6 листов приложений.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ …………………….……………………………………...2
1 Постановка задачи …………...………..…………………………3
2 Математическое описание методов …..……………..………..4
2.1 Метод хорд при приближенном вычислении алгебраических и трансцендентных уравнений ……..…………..………………..……..…..4
2.2 Решение системных линейных уравнений методом Зейделя …………..6
2.3 Решение дифференциальных уравнений методом Рунге-Кутта………...10
3 Блок-схема программы GLAV………………...…….....……...12
3.1 Блок-схема процедуры mhord……………………………....….……..13
3.2 Блок-схема процедуры myzend……………….………….…….…......14
3.3 Блок-схема процедуры mykutt……….…………………....……….......16
4 Описание стандартных модулей….…….…..………………...18
5 Описание не стандартных модулей….…………..…………...21
6 Описание интерфейса…….……………………………………..22
7 Численные примеры …..………….…...………………………..23
Заключение…………………………….......………………………..26
Список используемой литературы…..………………………....27
Приложение…………………………………………..………….….28
ВВЕДЕНИЕ
Студентам, а также инженерам часто требуется решать задачи, которые связаны с численными методами: решением алгебраических и трансцендентных уравнений, нахождение корня алгебраического уравнения, нахождение решений дифференциальных уравнений.
Подобные задачи решаются с помощью численных методов, разработанных для решения математических задач при помощи вычислительной техники на таких языках программирования, как: QBASIC, TURBO PASCAL, C++, DELPHI, VISUAL BASIC и д.р. пакеты программ. В частности, математические пакеты MathCAD, Maple, MathLab также дают возможность решения аналогичных задач.
Необходимо
учитывать, что вычислительная техника
не способна без погрешности записывать
такие величины как
 и т.д., погрешность может появляться и
при вычислении, округлении и других
операциях.
и т.д., погрешность может появляться и
при вычислении, округлении и других
операциях.
В некоторых случаях при вычислении необходимо предварительно математически преобразовать или переписать в другом виде функции, это может существенно снизить погрешность или в ряде случаев без преобразования не сходятся решения.
С помощью вычислительной техники можно решить и иные инженерные задачи, но с определенной погрешностью.
-
Постановка задач
Цель
данного курсового проекта – научиться
использовать методы структурного
программирования на примере численных
методов, в частности написание нескольких
модулей и связь их в одну общую программу.
1.1. Составить программу приближённого вычисления алгебраических и трансцендентных уравнений методом хорд 2х-3sin(2x)-1=0 и описать выше указанный метод, составить блок-схему, описать стандартные и не стандартные функции, применяемые в задаче, описать интерфейс и привести пример.
1.2. Составить программу для решения системы линейный уравнений методом Зейделя. Описать выше указанный метод, составить блок-схему, описать стандартные и не стандартные функции, применяемые в задаче, описать интерфейс и привести пример.

1.3. Составить программу для решения дифференциальных ур-й методом Рунге-Кутта.
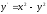

 шаг
0.1
шаг
0.1
Описать выше указанный метод, составить блок-схему, описать стандартные и не стандартные функции, а так же интерфейс задачи.
-
Математическое описание методов
2.1. Метод хорд
Идея
метода состоит в том, что по двум точкам
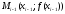 и
и
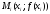 построить
прямую
построить
прямую
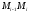 (то есть
хорду, соединяющую две точки графика
(то есть
хорду, соединяющую две точки графика
 )
и взять в качестве следующего приближения
)
и взять в качестве следующего приближения
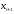 абсциссу
точки пересечения этой прямой с осью
абсциссу
точки пересечения этой прямой с осью
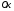 .
Иными словами, приближённо заменить на
этом шаге функцию
.
Иными словами, приближённо заменить на
этом шаге функцию
 её линейной
интерполяцией,
найденной по двум значениям
её линейной
интерполяцией,
найденной по двум значениям
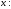
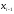 и
и
 .
(Линейной
интерполяцией
функции
.
(Линейной
интерполяцией
функции
 назовём
такую линейную функцию
назовём
такую линейную функцию
 ,
значения которой совпадают со значениями
,
значения которой совпадают со значениями
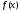 в
двух фиксированных точках, в данном
случае -- в точках
в
двух фиксированных точках, в данном
случае -- в точках
 и
и
 ).
).
В
зависимости от того, лежат ли точки
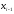 и
и
 по
разные стороны от корня
по
разные стороны от корня
 или же по
одну и ту же сторону, получаем такие
чертежи:
или же по
одну и ту же сторону, получаем такие
чертежи:
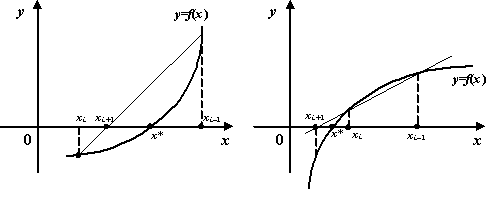
Случай 1
рис 1
Случай 2
рис 2
Построение последовательного приближения по методу хорд
8
Итак,
очередное последовательное приближение
будет зависеть от двух предыдущих:
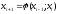 .
Найдём выражение для функции
.
Найдём выражение для функции
 .
.
Интерполяционную
линейную функцию
 будем
искать как функцию с угловым коэффициентом,
равным разностному отношению
будем
искать как функцию с угловым коэффициентом,
равным разностному отношению

построенному
для отрезка между
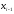 и
и
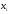 ,
график которой проходит через точку
,
график которой проходит через точку
 :
:

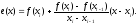
Решая
уравнение
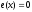 ,
находим
,
находим

то есть
 (1)
(1)
Заметим,
что величина
 может
рассматриваться как разностное
приближение для производной
может
рассматриваться как разностное
приближение для производной
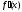 в
точке
в
точке
 .
Тем самым полученная формула (1) -- это
разностный аналог итерационной формулы
метода Ньютона.
.
Тем самым полученная формула (1) -- это
разностный аналог итерационной формулы
метода Ньютона.
Вычисление по формуле (1) гораздо предпочтительнее вычисления по другой полученной нами формуле
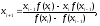
хотя
эти две формулы математически тождественны,
поскольку при использовании формулы
(1) в случае вычислений с округлениями
(например, на компьютере) достигается
меньшая потеря значащих цифр.
Имеются две разновидности применения формулы (1).
Первая
разновидность: вычисления ведутся
непосредственно по формуле (1) при
 ,
начиная с двух приближений
,
начиная с двух приближений
 и
и
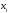 ,
взятых, по возможности, поближе к корню
,
взятых, по возможности, поближе к корню
 .
При этом не предполагается, что
.
При этом не предполагается, что
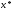 лежит
между
лежит
между
 и
и
 (и что значения функции
(и что значения функции
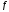 в
точках
в
точках
 и
и
 имеют
разные знаки). При этом не гарантируется,
что корень попадёт на отрезок между
имеют
разные знаки). При этом не гарантируется,
что корень попадёт на отрезок между
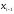 и
и
 на
каком-либо следующем шаге (хотя это и
не исключено). В таком случае затруднительно
дать оценку погрешности, с которой
на
каком-либо следующем шаге (хотя это и
не исключено). В таком случае затруднительно
дать оценку погрешности, с которой
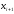 приближает
истинное значение корня
приближает
истинное значение корня
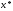 ,
и поэтому довольствуются таким
эмпирическим правилом: вычисления
прекращают, когда будет выполнено
неравенство
,
и поэтому довольствуются таким
эмпирическим правилом: вычисления
прекращают, когда будет выполнено
неравенство
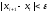 ,
где
,
где --
желаемая точность нахождения корня.
При этом полагают приближённое значение
корня равным
--
желаемая точность нахождения корня.
При этом полагают приближённое значение
корня равным [1].
[1].
