Распромтанение плоской волны.

Идеальными называют диэлектрик, проводимость которого равна нулю. Например, нижние слои атмосферы во многих случаях можно считать идеальным диэлектриком.

Рассмотрим распространение плоской электромагнитной волны в идеальном диэлектрике, считая, что= const и. Параметры волны запишутся следующим образом. Коэффициент поглощения а = 0, и поэтому коэффициент распространения является мнимым числом:

Коэффициент фазы

Фазовая скорость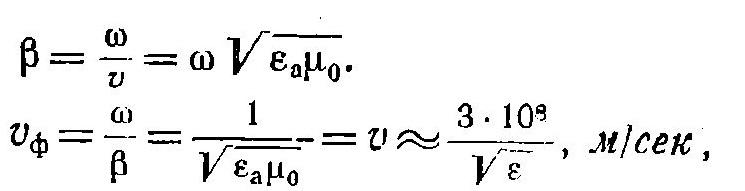равна скорости распространения электромагнитной энергии.

В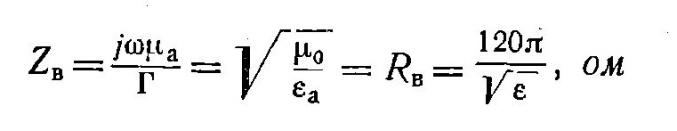олновое сопротивление

является вещественным числом.

У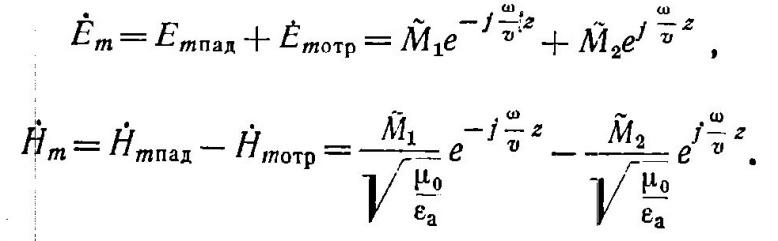равнения и примут следующий вид

М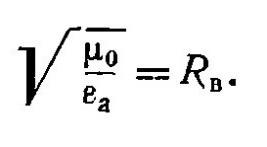ожно обозначить:

Если среда не ограничена в направлении распространения, то мгновенные значения векторов поля определяются ординатами прямой или падающей волны, постоянная = 0.

Пусть при тогда

,

,

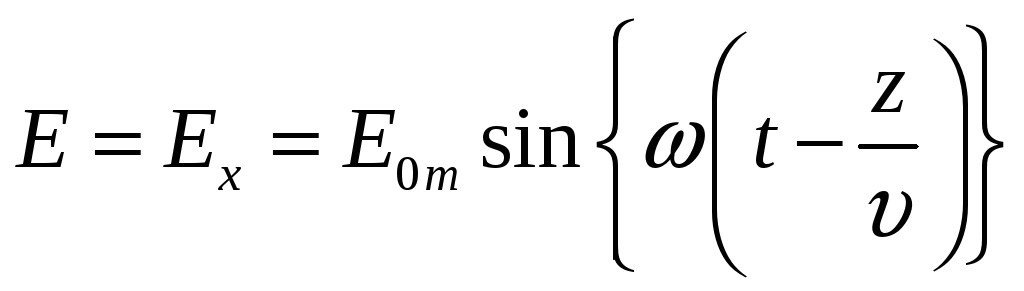Падающие волны напряженности электрического и напряженности магнитного полей.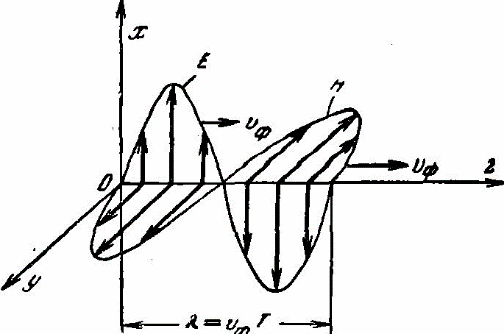

На рис. 5-2 изображены кривые зависимости идля фиксированного момента времени t.

Покажем, что энергия электрического поля в объеме V равна энергии магнитного поля в том же объеме:

Вместе с плоской волной в направлении оси z переме-щается энергия, излучаемая источником поля. Через площадку в 1 м2 перпендикулярную оси z, проходит за 1 сек. энергия, численно равная значению вектора Пойн-тинга на этой площадке.

Полученные результаты показывают, что амплитуды векторов поля неизменны и, следовательно, волна распро-страняется без затухания (среда непоглощающая).

Волны Е и Н, распространяясь с одинаковой скоростью

совпадают по фазе (так как волновое сопротивление-число вещественное. Скорость распространения не зависит от частоты. Отношения комплексных амплитуд векторов поляравно волновому сопротивлению

Распространение плоской волны в хорошо проводящей среде

В хорошо проводящей среде токи проводимости значительно больше токов смещения и поэтому последним можно пренебречь. При определении параметров волны можно положить

К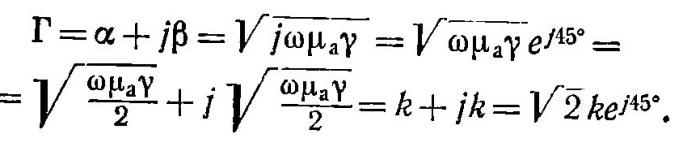оэффициент распространения при этом равен:

Следовательно, коэффициент поглощения при этом равен коэффициенту фазы.

Волновое сопротивление примет вид:

Фазовая скорость

Длина волны определится из выражения

Если среда не ограничена в направлении распространения, то мгновенные значения векторов поля

В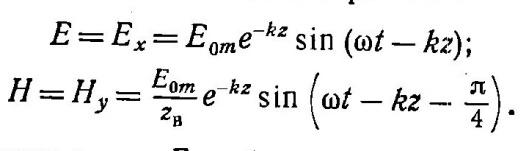этих выраженияхобозначает амплитуду вектора Е в точке z=0 . Величинапринята равной нулю. Амплитуды векторов поля уменьшаются в направлении распространения. Определим среднюю за период мощность тепловых потерь в объеме V и покажем, что она равна потоку среднего значения вектора Пойнтинга сквозь выбранную поверхность S.

Рис. 5-3. Вычисление потерь в поглощающей среде..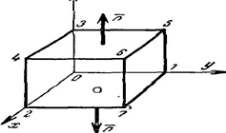

Пусть S — замкнутая поверхность, ограничивающая объем V параллелепипеда (рис. 5-3). Среда хорошо проводящая, ее проводимость и магнитная проницаемость=const заданы . Плоская гармоническая волна с частотойраспространяется в направлении оси z.

В случае плоской волны, распространяющейся без отражения в хорошо проводящей среде,

Коэффициент затухания и коэффициент фазы в этом случае равны друг другу и определяются выражением:

Искомая мощность равна:

.

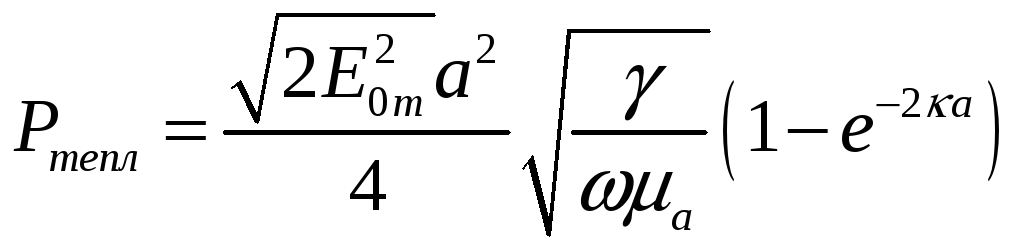Среднее значение вектора Пойнтинга за период:

Так как векторы в рассматриваемом случае имеют по одной проекции, то

и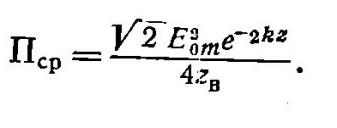вектор Пойнтинга имеет одну проекцию. Следовательно:

Волновое сопротивление хорошо проводящей среды равно по абсолютной величине

Подставив это значение, получим:

П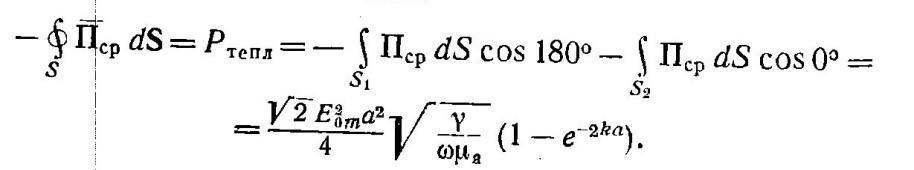оток вектора Пойнтинга отличен от нуля только сквозь площадки 01720 =и 35643 =( рис. 5-3). По теореме Умова-Пойнтинга

В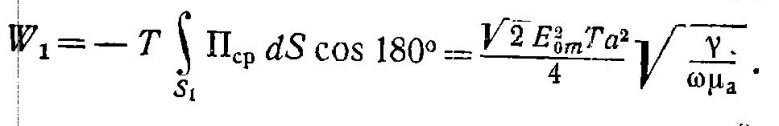ычисленный поток оказался равным средней мощности тепловых потерь. Энергия, которая входит в выбранный объем за некоторое время, например, за период Т, равна:

Э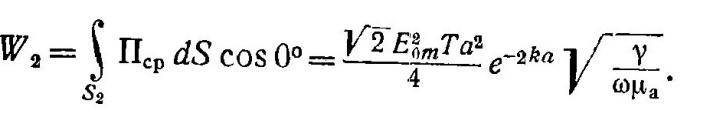нергия, которая выходит из этого объема за то же время, равна:

Э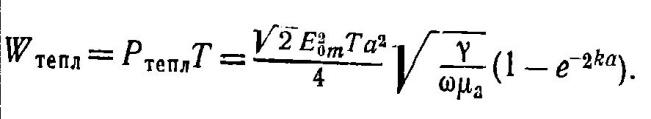нергия тепловых потерь в объеме V за то же время равна:

Сравнивая величины этих энергий, получаем:

Анализируя полученные результаты, приходим к сле-дующему выводу. В хорошо проводящей средеволны Е и Н распространяются с одинаковой скоростью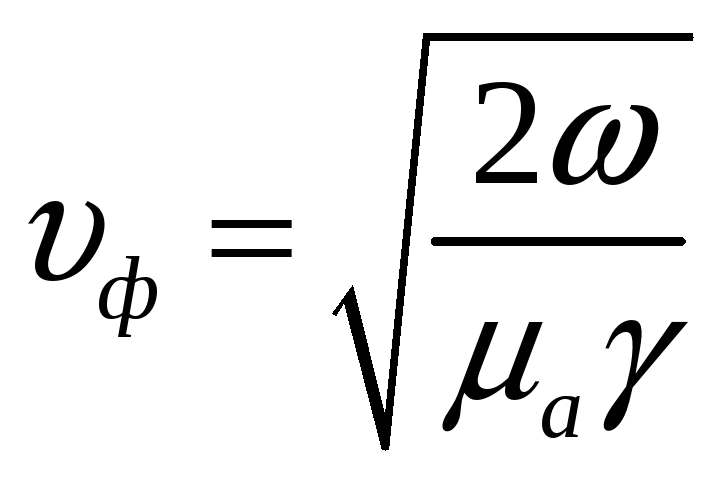которая зависит от частоты.

Амплитуды векторов поля затухают в направлении распространения, что вызывается поглощением энергии средой (тепловые потери). Быстрота затухания амплитуд характеризуется множителем, где

(5-9)

На расстоянии, равном длине волны , векторы поля практически обращаются в нуль, так какОтношение комплексных амплитудиравное вол-новому сопротивлению, число комплексное:

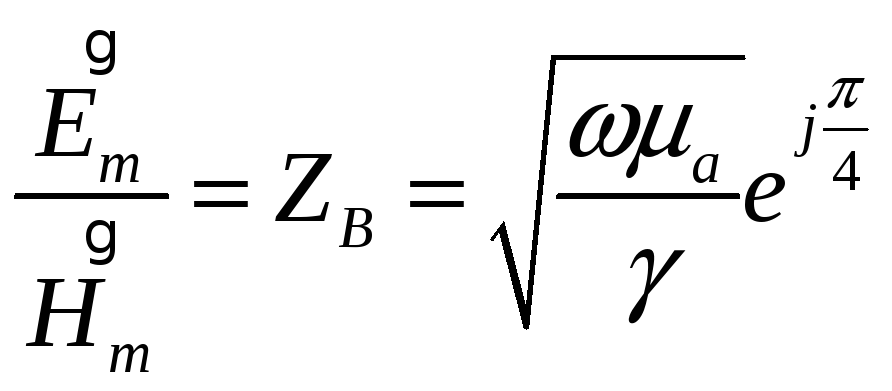
Следовательно, волны E и H сдвинуты по фазе на

Значения параметров волны для различных сред представлены в табл. 5-1.