2. Наклонное падение плоской волны

Пусть направление распространения плоской гармонической волны составляет с граничной плоскостью между двумя разнородными средами угол, отличный от прямого. Обе среды — идеальные диэлектрики.

Н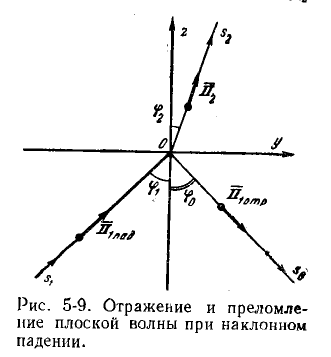аправление распространения падающей волны в первой среде обозначим черезs₁.

Волна, встретив граничную поверхность, частично отразится от нее, частично перейдет во вторую среду.

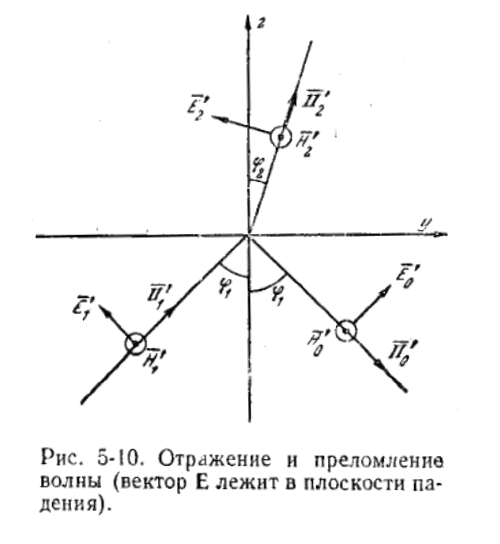
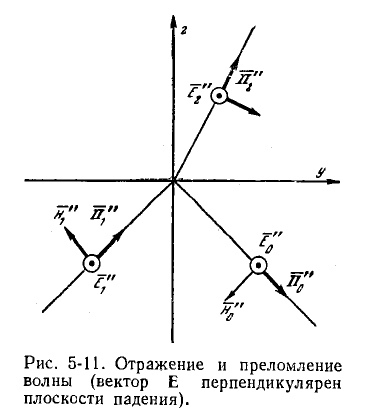
Направления распространения отраженной и преломленной волн обозначим через s₀иs₂. Назовем плоскостью падения плоскость, на которой лежат вектор Пойнтинга падающей волны и нормаль к граничной плоскости.

На рисунке координатные оси х, у, zнаправлены таким образом, чтобы плоскость уОх совпала с граничной, а пло­скость уОzсовпала с плоскостью падения.

Угол φ₁между направлением распространения падающей волныs₁и нормалью к граничной плоскости (в данном слу­чае с осьюz)называютуглом падения. Угол φ₀между направлением распространения отраженной волныs₀и нормалью к граничной плоскости называютуглом отражения. Угол называютуглом преломления.

Расстояние r₁плоскости постоянной фазы падающей волны до начала координат в общем случае равно:

причём

Так как при выбранном на рисунке направлении коор­динатных осей cos(s₁,х) = 0, уголs₁Oz= φ₁, то

Аналогично можно записать и расстояния от начала координат до плоскости равных фаз отраженной и преломленной волн:

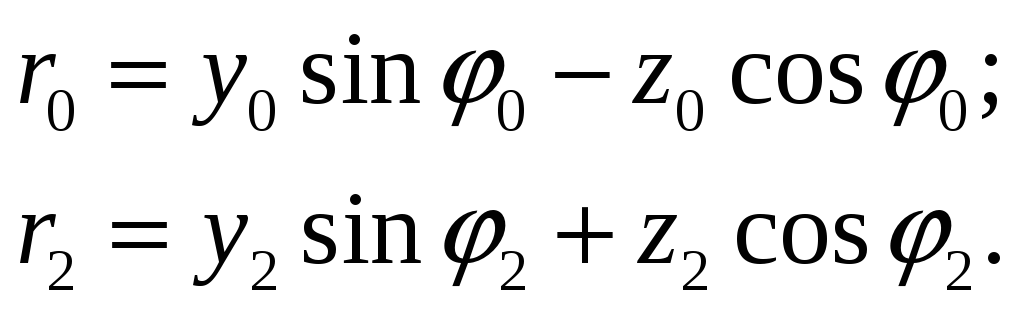
Мгновенные значения напряженностей электрического и магнитного поля всех трех волн можно записать следующим образом:

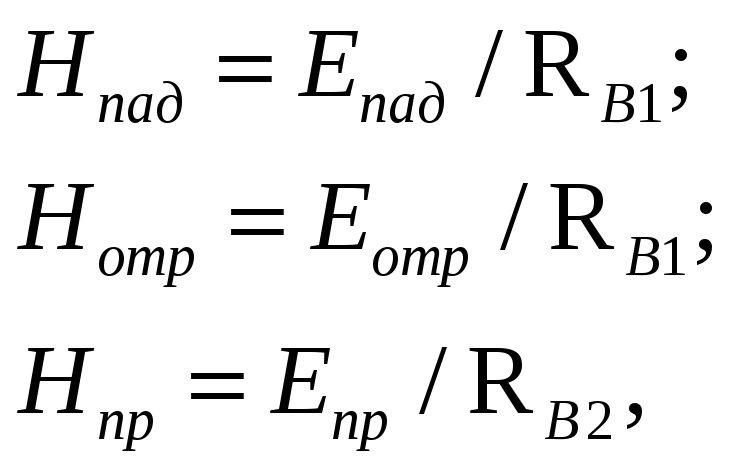
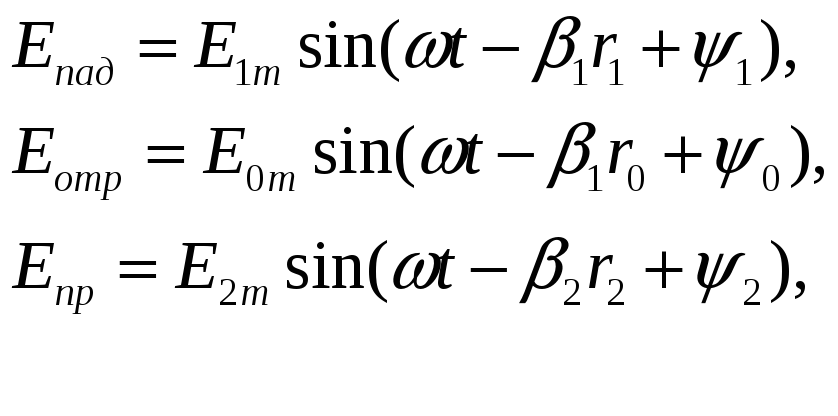
где

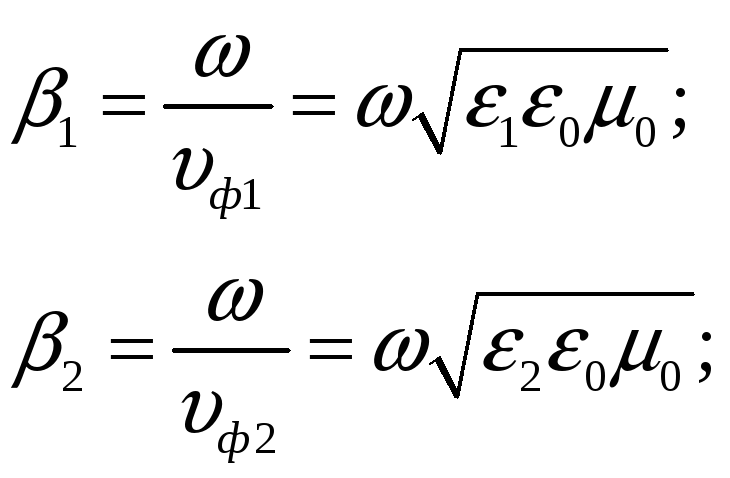
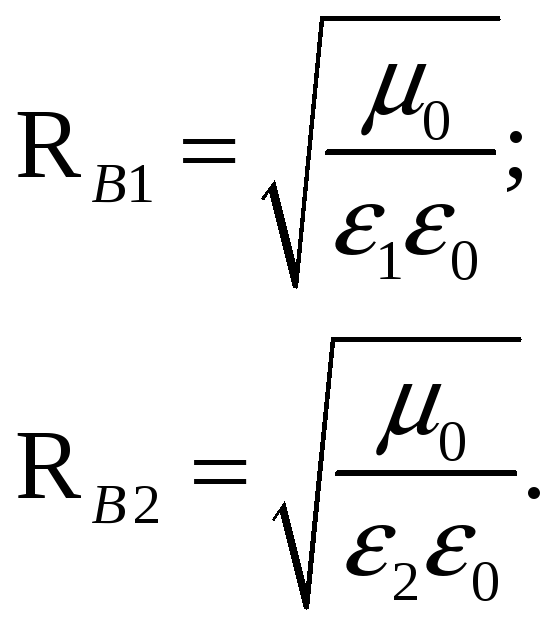
Им соответствуют комплексные амплитуды

На граничной плоскости при z= 0 тангенциальные со­ставляющие вектора Е непрерывны:

Так как при z= 0

r₁ = ysinφ₁;

r₀ = y sin φ₀;

r₂ = y sin φ₂,

то

Граничное условие будет соблюдено только в том слу­чае, если

Полученное выражение позволяет формулировать два закона.

а) Угол падения равен углу отражения (закон отражения):

б) Отношение синуса угла падения к синусу угла прелом­ления—величина постоянная,равная отношению фазовых скоростей в первой и второй средах (закон преломления):

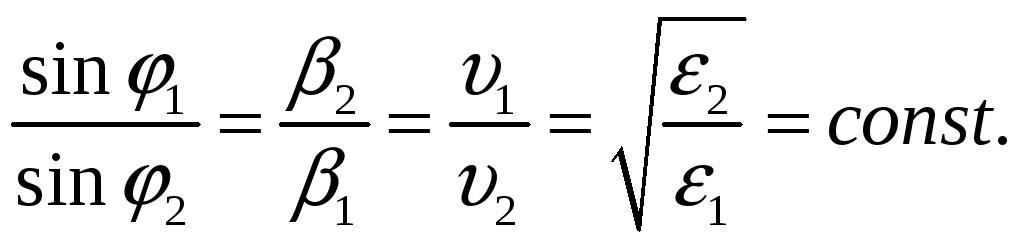
Закон отражения справедлив для плоских волн любой поляризации и при разных частотах. Что касается закона преломления, то, так как диэлектрическая проницаемость среды, а следовательно, и фазовая скорость волны зависят от частоты (явление дисперсии), то отношение синусов углов падения и преломления, постоянное при фиксированной частоте, меняется при изменении частоты.

Зная амплитуду и фазу Е_пади диэлектрические прони­цаемости обеих сред, можно, используя граничные условия, найтиЕ_отриЕ_пр. Вначале будут рассмотрены два частных случая:

1. когда Е_пад совпадает с плоскостью падения;

2. когда Е_пад перпендикулярен плоскости падения.

Установив законы отражения и преломления в этих двух случаях, можно определить их и в случае произвольного направления Е_пад. Для этого надо разложить Е_падна два взаимно перпендикулярных вектора, один из которых должен совпадать с плоскостью падения, и воспользоваться принципом наложения.

1. Пусть вектор Е' лежит в плоскости падения. Тогда вектор Н' будет параллелен оси х.

Выберем для векторов H’₁, Н₀’ и Н₂’ положительное на­правление, совпадающее с направлением осих.

Так как на граничной плоскости нет поверхностных то­ков, то тангенциальные составляющие вектора Н' по обе стороны граничной поверхности при z=0 и любомхдолж­ны быть одинаковы. Следовательно, должны быть одина­ковы и их комплексные амплитуды:

Тангенциальные составляющие вектора Ена границе также должны быть одинаковыми:

Так как , ато, решив совместно оба уравнения, получим:

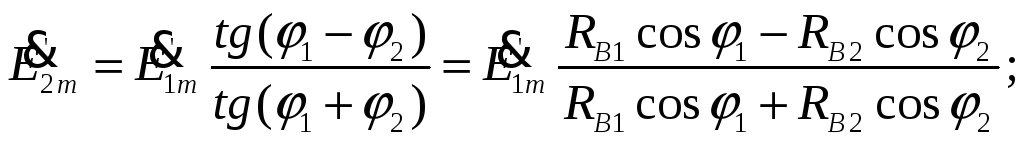
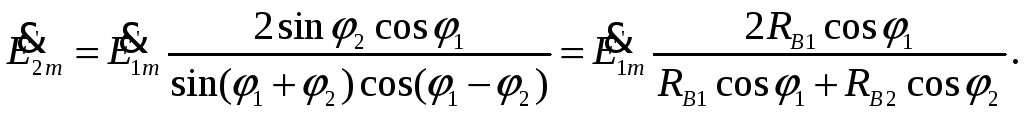
Полученные формулы носят название формул Френеля. Они позволяют определить комплексные амплитуды век­торов поля отраженной и преломленной волн по известной комплексной амплитуде напряженности электрического поля падающей волны .Штрих в выражении комплексных амплитуд указывает на то, что рассматривается частный случай, когдаЕлежит в плоскости падения.

Отношение называется коэффициентом отражения в этом частном случае.

Отношение называется коэффициентом прохождения (преломления).

2. Пусть вектор Еперпендикулярен плоскости падения , т. е. при выбранном направлении координатных осей параллелен осих.Вектор Н будет расположен в пло­скостиxOz.Положительное направление для векторовЕ, Е₀иЕ₂выбираем параллельно осих.Граничные условия (приz= 0) следующие:

Так как , то, решив эти уравнения, получим формулы Френеля для рассматриваемого частного случая:

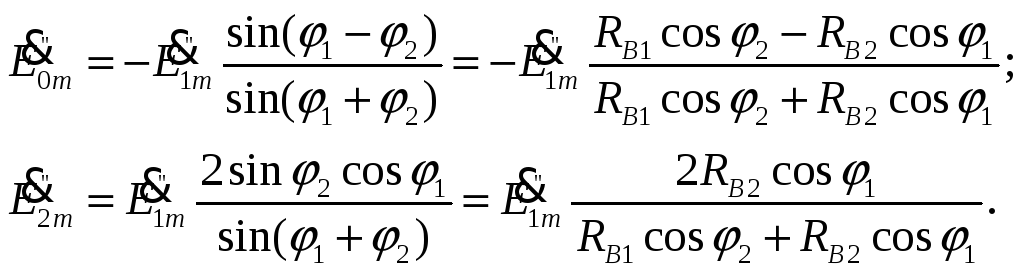
Коэффициент отражения в этом частном случае равен

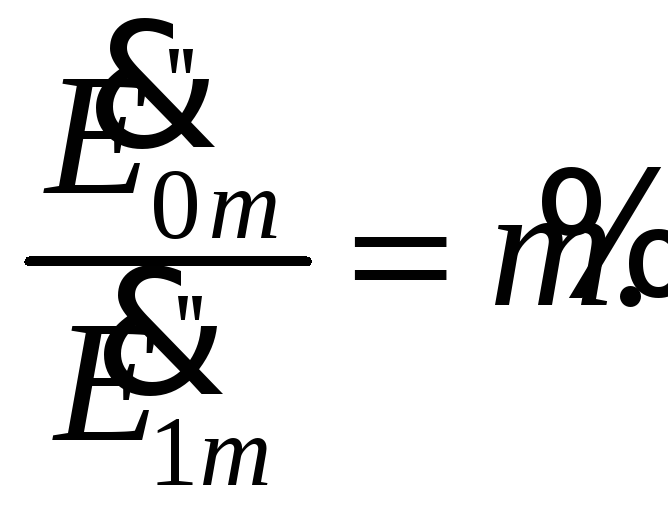
Коэффициент прохождения (преломления) равен