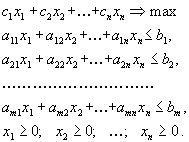- •1 Этапы построения математической модели
- •2 Геометрическая интерпретация задачи лп
- •3 Геометрическая интерпретация задачи лп по целевой функции
- •4 Векторный вид канонической формы задачи лп
- •5 Скалярный вид задачи лп
- •6 Специальная форма лп (Симплекс метод)
- •7 Базисное решение
- •7* Базисное допустимое решение
- •7* Базисное недопустимое решение
- •8 Вырожденное базисное решение
- •9 Оптимальная симплекс таблица
- •10 Неразрешимость задачи лп
- •18 Условие дополняющей нежесткости для транспортной задачи
- •19 Условия при которых задача относится к динамическому программированию
- •20 Уравнение состояния Беллмана
- •21 Общий вид Уравнения Бэллмана
- •29 Задача лп для первого игрока матричной игры
1 Этапы построения математической модели
Составление математической модели начинают с выбора переменных, совокупность числовых значений которых однозначно определяет один из вариантов процесса. Следует иметь в виду, что иной раз от удачного выбора этих переменных зависит простота модели и, следовательно, удобство дальнейшего ее анализа.
После выбора переменных необходимо составить ограничения по тексту задачи, которым эти переменные должны удовлетворять. При этом нужно следить, чтобы в модель были включены все ограничительные условия, и в то же время не было ни одного лишнего или записанного в более жесткой, чем требуется условиями задачи, форме.
Наконец, составляется целевая функция, которая в математической форме отражает критерий выбора лучшего варианта.
После составления математической модели необходимо рассмотреть возможные пути ее упрощения и выбрать подходящий вычислительный метод для решения задачи.
2 Геометрическая интерпретация задачи лп
Строя на плоскости прямые по ограничениям получает допустимую область ограниченную выпуклым многоугольником построенным на точках пересечения прямых.
Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника ( см. рис. 6).
Неосновной случай получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 7. Подобная ситуация, например, получится, если в рассмотренном выше примере убрать ограничение
 .
Оставшаяся часть будет неограниченным
выпуклым многоугольником.
.
Оставшаяся часть будет неограниченным
выпуклым многоугольником.

Наконец, возможен случай, когда неравенства (1.22) противоречат друг другу, и допустимая область вообще пуста.
3 Геометрическая интерпретация задачи лп по целевой функции
Строим прямую на плоскости по уравнению целевой функции и указываем её направление (max,min), передвигает прямую параллельно себе в границе допустимой области в направлении функции.
Возможны варианты
- функция выйдет за пределы допустимой области на пересечении 2 прямых из ограничений(тогда точка пересечения будет являться оптимальным значением целевой функции )
- прямая выйдет параллельно какой-то прямой из ограничений(оптимальным значением будут точки пересечения этой прямой с другими)
- если область допустимых значений неограниченна то значение целевой функции тоже будет неограниченно
4 Векторный вид канонической формы задачи лп
Каноничная форма ЗЛП

В векторной форме:

В матричной форме:
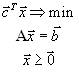
Во
всех этих задачах функцию ![]() называютцелевой
функцией.
Вектор
называютцелевой
функцией.
Вектор ![]() называютвектором
коэффициентовлинейной
формы, вектор
называютвектором
коэффициентовлинейной
формы, вектор ![]() вектором
ограничений.
вектором
ограничений.
|
Матрицу |
называют матрицей коэффициентов. |
Любой набор чисел ![]() ,
удовлетворяющий ограничениям задачи,
называютпланом,
а множество всех планов допустимой
областью. Тот план,
который доставляет экстремум (минимум
или максимум) целевой функции,
называют оптимальным
планом или
просто решением задачи
линейного программирования.
,
удовлетворяющий ограничениям задачи,
называютпланом,
а множество всех планов допустимой
областью. Тот план,
который доставляет экстремум (минимум
или максимум) целевой функции,
называют оптимальным
планом или
просто решением задачи
линейного программирования.
5 Скалярный вид задачи лп
|
Первая форма |
Вторая форма |
Каноническая форма |
|
|
|
|
6 Специальная форма лп (Симплекс метод)

7 Базисное решение
Записанная в стандартной форме задача линейного программирования содержит m линейных равенств и n неизвестных переменных, причем m < n. Разделим эти переменные на два множества: n − m равных нулю и m, определенных как решение соответствующей системы. Если это решение единственное – назовем эти переменные базисными, а остальные – небазисными. В этом случае получившееся решение называется базисным решением. Если при этом все переменные неотрицательны, то такое решение называемдопустимым, а в противном случае –недопустимым.//т. e. грубо говоря вектор который мы получаем когда получаем допустимое решение в симплекс таблице