Аннотация

В работе строится математическая модель для минимизации затрат времени на производство. Для полученной задачи линейного программирования рассчитывается оптимальный план распределения устройств симплекс-методом. Результат решения для исследуемой модели может быть использован на производстве при выполнении более сложных расчетов в новой модели целочисленной задачи.

Реферат

Ключевые слова: ЗАДАЧА О РАСПРЕДЕЛЕНИИ, ОПТИМИЗАЦИЯ, МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ, СИМПЛЕКС-МЕТОД, МЕТОД ГОМОРИ

Курсовая работа по дисциплине «Методы оптимизации». Объектом исследования была задача «О распределении» с необходимостью найти оптимальный план распределения, при ограниченных средствах и времени.

Содержание

Введение……………………………………………………………………………….3

1 Методы оптимизации……………………………………………………………….4

2 Постановка задачи оптимизации…………………………………………………...4

3 Построение математической модели………………………………………………4

3.1 Определение переменных………………………………………………………...4

3.2 Графическое представление математической модели………………………….4

3.3 Установка ограничений…………………………………………………………...4

3.4 Подстановка чисел………………………………………………………………...5

4. Решение поставленной задачи……………………………………………………..5

4.1 Решение симпликс-методом………………………………………………………5

4.2 Решение методом Гомори…………………………………………………………9

4.3 Решение двойственным симплекс-методом…………………………………….13

Заключение……………………………………………………………………………17

Библиографический список………………………………………………………….18

Введение

Целью курсовой работы является проверка и применение теоретических знаний полученных за курс по дисциплине «Методы оптимизации». Объект исследования задача «О распределении» с необходимостью найти оптимальный план распределения, при ограниченных средствах и времени. В работе будут применены основные методы для решения поставленной задачи, такие как: симплекс-метод, метод Гомори и двойственный симплекс-метод. Для удобного представление решения используется программа для работы с электронными таблицами MS Excel.

1. Методы оптимизации.

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств [2].

Теорию и методы решения задачи оптимизации изучает математическое программирование.

Математическое программирование – это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных [3].

2. Постановка задачи оптимизации.

Задача о распределении устройств

Предприятие планирует ремонт технических устройств в количестве n штук в трех мастерских. Затраты на ремонт технических устройств в различных мастерских различны, время различно. Средства на ремонт ограничены.

Составить план распределения технических устройств по мастерским так, чтобы суммарное время на ремонт было минимально.

2. Построение математической модели.

3.1 Определение переменных.

x_i – количество устройств в i мастерской. i = 1, 2, 3.

a_i – стоимость ремонта одного технического устройство в i-ой мастерской.

t_i – время ремонта одного технического устройство в i-ой мастерской.

S – суммарная стоимость ремонта всех технических устройств в 3-х мастерских.

3.2 Графическое представление математической модели. (Рисунок 1)

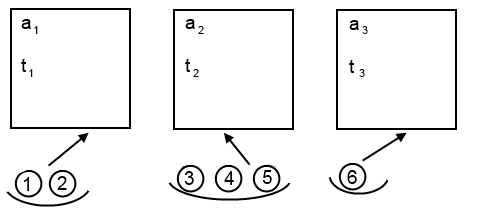
Рисунок 1 – Графическое представление

3.3 Установка ограничений.

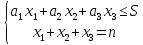
3.4 Подстановка чисел.

Подстановка чисел осуществляется путем добавлением численных значений в поставленную задачу.

Предприятие планирует ремонт технических устройств в количестве 6 штук в трех мастерских. Затраты на ремонт технических устройств в различных мастерских различны a₁=5, a₂=4, a₃=6, время различно t₁=3, t₂=4, t₃=2. Средства на ремонт ограничены S = 30.

Составить план распределения технических устройств по мастерским так, чтобы суммарное время на ремонт было минимально.

4. Решение поставленной задачи.

Решение поставленной задачи можно осуществить используя 3 метода: симплекс-метод (п. 4.1), метод Гомори (п. 4.2), двойственным симплекс-методом (п. 4.3).

4.1 Решение симпликс методом.

Симплекс-метод – это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения [4].

Для удобного представление решения используется программа для работы с электронными таблицами MS Excel. В помощь было взято учебное пособие [1].

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-ом неравенстве вводим базисную переменную x₄:

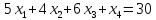
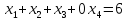
Введем искусственную переменную x₅ во 2-ое равенство:

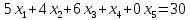
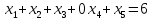
Для постановки задачи на минимум целевую функцию запишем так:

Получений базис называется искусственным, а метод решения называется методом искусственного базиса.

Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.

Из уравнений выражаем искусственные переменные, которые подставляем в целевую функцию:

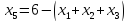
Базисные переменные – это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Базисное решение называется допустимым, если оно неотрицательно.

Далее, строим симплекс-таблицу для нахождения оптимального решения поставленной задачи (Таблица 1).

Таблица 1 – Начальная симплекс-таблица

Далее переходим к основному алгоритму симлекс-метода.

Проводим итерацию №0 для проверки критерия оптимальности.

Проверка критерия оптимальности.

Текущий опорный план не оптимален, так как в индексной строке находятся положительные коэффициенты.

Далее переходим определению новой базисной переменной.

В качестве ведущего выберем столбец, соответствующий переменной x₃, так как это наибольший коэффициент.

Далее переходим пределению новой свободной переменной.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i3 и из них выберем наименьшее:

Следовательно, 1-ая строка является ведущей.

Разрешающий элемент равен (6) и находится на пересечении ведущего столбца и ведущей строки (Таблица 2).

Таблица 2 – Симплекс-таблица с выделенным разрешающим элементом

Далее проводим пересчет симплекс-таблицу по разрешающему элементу (Таблица 3).

Таблица 3 – Симплекс-таблица после совершения итерации №0

Проводим итерацию №1 для проверки критерия оптимальности.

Текущий опорный план не оптимален, так как в индексной строке находятся положительные коэффициенты.

Далее переходим к определению новой базисной переменной.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент.

Далее переходим к определению новой свободной переменной.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2 и из них выберем наименьшее:

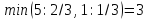
Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (¹/₃) и находится на пересечении ведущего столбца и ведущей строки (Таблица 4).

Таблица 4 – Симплекс-таблица с выделенным разрешающим элементом

Проводим пересчет симплекс-таблицу по разрешающему элементу (Таблица 5).

Таблица 5 – Симплекс-таблица после совершения итерации №0

Среди значение индексной строки нет положительных элементов. Поэтому эта таблица определяет оптимальный план задачи.

Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.

Оптимальный план можно записать так:

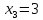
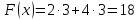
Как следствие, используя симплекс-метод, установлено, что для минимизации времени ремонта нам необходимо распределить устройства следующим образом: в мастерскую №1 будет направленно устройств в количестве 0 шт., в мастерскую №2 будет направленно устройств в количестве 3, в мастерскую №3 будет направленно устройств в количестве 3. При этом минимальное время для ремонта всех устройств будет равно 18.