Методы оптимизации
Задача о оптимизации использования
Методы оптимизации
Суть методов оптимизации заключается в том, чтобы, исходя из наличия
определенных ресурсов, выбрать такой способ их
использования , при
котором будет обеспечен максимум или минимум интересующего
показателя.
Постановка задачи
Требуется распилить N брёвен
длиной Li , I = 1 ,N;
Каждое на брусья трёх размеров 3,5 ; 4,5 и 5 м.
Задача
Составить модель для определения
оптимального плана распила из условия
максимального числа брусьев в заданном
ассортименте
Математическая модель
Xi1, Xi2 , Xi3 – кол-во брёвен определённого типа
Длинны
Ограничения
X1,2,3 >= 0
3,5*Xi1 + 4,5*Xi2 + 5*Xi3 + 1*X4 + 0*X5 = 18
3,5*Xi1 + 4,5*Xi2 + 5*Xi3 + 0*X4 + 1*X5 = 22
Решение
Для решения данной задачи будем использовать симпликс метод.
Приведение к канонической форме
Сначала необходимо привести задачу к канонической форме, для этого введём базисную переменную
3.5x1 + 4.5x2 + 5x3 + 1x4 + 0x5 = 18 3.5x1 + 4.5x2 + 5x3 + 0x4 + 1x5 = 22
Симпликс таблица
В составленной симпликс таблице выберем
разрешающий элемент.
Для этого в строке цел. Функции в качестве разрешающего столбца
выберем максимальный по модулю элемент. Выберем разрешающую строку.
Вычислим значения Di по строкам как частное от деления: bi / ai1 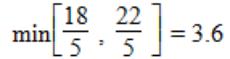 наименьшее:
наименьшее:
Следовательно, 1-ая строка является ведущей.


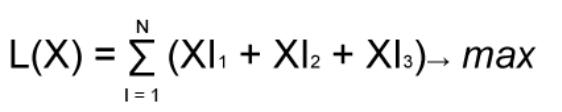

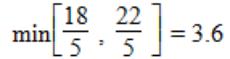 наименьшее:
наименьшее: