
Методы оптимизации Зыкина
.docx-
Методы оптимизации.
Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
Теорию и методы решения задачи оптимизации изучает математическое программирование.
Математическое программирование - это область математики, разрабатывающая теорию, численные методы решения многомерных задач с ограничениями. В отличие от классической математики, математическое программирование занимается математическими методами решения задач нахождения наилучших вариантов из всех возможных.
-
Постановка задачи оптимизации.
Задача о распределении устройств
Предприятие планирует ремонт технических устройств в количестве n штук в трех мастерских. Затраты на ремонт технических устройств в различных мастерских различны, время различно. Средства на ремонт ограничены.
Составить план распределения технических устройств по мастерским так, чтобы суммарное время на ремонт было минимально.
-
Построение математической модели.
3.1 Определение переменных.
xi – количество устройств в i-ой мастерской. i = 1, 2, 3.
ai – стоимость ремонта одного технического устройство в i-ой мастерской.
ti – время ремонта одного технического устройство в i-ой мастерской.
S – суммарная стоимость ремонта n-го количества технических устройств в 3-х мастерских.
3.2 Графическое представление математической модели.
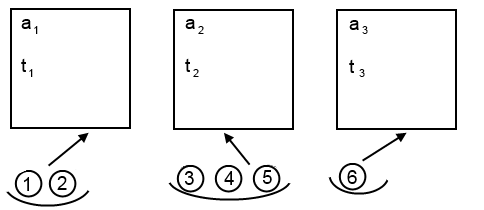
3.3 Установка ограничений.
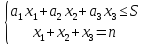
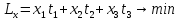
3.4 Подстановка чисел.
Предприятие планирует ремонт технических устройств в количестве 6 штук в трех мастерских. Затраты на ремонт технических устройств в различных мастерских различны a1=5, a2=4, a3=6, время различно t1=3, t2=4, t3=2. Средства на ремонт ограничены S = 30.
Составить план распределения технических устройств по мастерским так, чтобы суммарное время на ремонт было минимально.
4. Решение поставленной задачи.
4.1 Решение симпликс методом.
Симплекс-метод – это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения.
Для удобного представление решения используется программа для работы с электронными таблицами MS Excel.
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-ом неравенстве вводим базисную переменную x4:


Введем искусственную переменную x5 во 2-ое равенство:
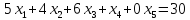

Для постановки задачи на минимум целевую функцию запишем так:

Получений базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные, которые подставляем в целевую функцию:
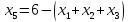
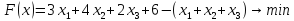
Базисные переменные – это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Базисное решение называется допустимым, если оно неотрицательно.

Переходим к основному алгоритму симлекс-метода.
Итерация №0.
Проверка критерия оптимальности.
Текущий опорный план не оптимален, так как в индексной строке находятся положительные коэффициенты.
Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент.
Определение новой свободной переменной.
Вычислим значения
Di по
строкам как частное от деления: bi /
ai3
и
из них выберем наименьшее:
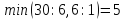
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (6) и находится на пересечении ведущего столбца и ведущей строки.
Пересчитаем симплекс-таблицу.

Итерация №1. Проверка критерия оптимальности.
Текущий опорный план не оптимален, так как в индексной строке находятся положительные коэффициенты.
Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент.
Определение новой свободной переменной.
Вычислим значения
Di по
строкам как частное от деления: bi /
ai2
и
из них выберем наименьшее:
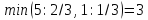
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (1/3) и находится на пересечении ведущего столбца и ведущей строки.
Пересчитаем симплекс-таблицу:

Среди значение индексной строки нет положительных элементов. Поэтому эта таблица определяет оптимальный план задачи.
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.
Оптимальный план можно записать так:
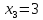

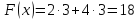
Так как решение получилось целочисленным. Нет необходимости применять метод Гомори.
Также для данной задачи использование двойственного метода – нецелесообразно.
Следовательно, для минимизации времени ремонта нам необходимо распределить устройства следующим образом: в мастерскую №1 – 0, в мастерскую №2 – 3, в мастерскую №3 – 3. При этом время будет равно 18.
