1. Определить количество строк и столбцов в таблице истинности.

Т.к. каждое из простых высказываний может принимать всего два значения (0 или 1), то количество разных комбинаций значений n высказываний – 2 ⁿ .

Количество строк в таблице = 2 ⁿ + строка на заголовок.

Количество столбцов в таблице равно сумме количества простых высказываний (n) и количества разных логических операций, входящих в сложное высказывание.

В нашем примере: количество строк - 2² + 1 = 5 ,

столбцов – 2 + 4 = 6

2. Начертить таблицу и заполнить заголовок

Первая строка – номера столбцов.

Вторая строка промежуточные формулы и соответствующие им условные записи операций над значениями .

3. Заполнить первые n столбцов.

В нашем примере сначала заполняем 1-й и 2-й столбцы.

4. Заполнить остальные столбцы.

В соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого.

Итак, вычисляем значения 3-го столбца по значениям 2-го, потом значения 4-го – по значениям 1-го и 2-го…

К	С	 С	К  C	( К  C ) &  С	( К  C ) &  С  К
1	1	0	1	0	1
0	1	0	1	0	1
1	0	1	1	1	1
0	0	1	0	0	1

Вывод: получили в последнем столбце все единицы. Значит, значение сложного высказывания истинно при любых значениях простых высказываний К и С. Следовательно, учитель рассуждал логически правильно.

СДНФ (Совершенная Дизъюнктивная Нормальная Форма) — это такая ДНФ, которая удовлетворяет трём условиям:

• в ней нет одинаковых элементарных конъюнкций

• в каждой конъюнкции нет одинаковых пропозициональных букв

• каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.

Для любой функции алгебры логики существует своя СДНФ, причем единственная.

СКНФ (Совершенная Конъюнктивная Нормальная Форма) — это такая КНФ, которая удовлетворяет трём условиям:

• в ней нет одинаковых элементарных дизъюнкций

• в каждой дизъюнкции нет одинаковых пропозициональных переменных

• каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.

Совершенная конъюнктивная нормальная форма (СКНФ): 1) нет двух элементарных дизъюнкций; 2) ни одна элементарная дизъюнкция не содержит двух одинаковых переменных; 3) ни одна элементарная дизъюнкция не содержит переменную вместе с ее инверсией; 4) все дизъюнкции имеют один и тот же ранг.	Совершенная дизъюнктивная нормальная форма (СДНФ)
Алгоритм образования СКНФ и СДНФ по таблице истинности
1. Выделить в таблице истинности все строки, в которых функция принимает значения 0.	1. Выделить в таблице истинности все строки, в которых функция принимает значения 1.
2. Для каждого выбранного набора записать элементарные дизъюнкции, содержащие переменные: а) если значение переменной равно 0, то записывается сама переменная, б) если значение переменной равно 1, то записывается инверсия этой переменной.	2. Для каждого выбранного набора записать элементарные конъюнкции, содержащие переменные: а) если значение переменной равно 0, то записывается инверсия этой переменной, б) если значение переменной равно 1, то записывается сама переменная.
3. Соединить элементарные дизъюнкции знаком конъюнкции.	3. Соединить элементарные конъюнкции знаком дизъюнкции.

Полином Жегалкина — многочлен над кольцом , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения —исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).

Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.

Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде

или в более формализованном виде как:

Примеры полиномов Жегалкина:

5.

Аксиомы исчисления высказываний

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

Правил вывода в ИВ имеется два. Первое из них, называемое правилом заключения или modus ponens (сокращенно mod pon) дает по паре формул Ф и Ф  Ψ формулу Ψ, или, в функциональных обозначениях,

R₁ (Ф, Ф  Ψ) = Ψ.

Таким образом, mod pon – это функция двух переменных, причем определенная не всюду, а только для пар формул, очевидным образом согласованных друг с другом.

Второе из правил вывода – это правило подстановки. Операция подстановки Ψ естественно определяется для произвольных слов. Итак, пусть Ф и Ψ – слова в некотором алфавите А, а x – буква того же алфавита. Результатом подстановки слова Ψ вместо буквы х в слово Ф, обозначаемым S^х _Ψ Ф, называют слово, получающееся из Ф в результате замены каждого вхождения в него буквы х на слово Ψ. Например,

S^л_жирофл леля = жирофлежирофля.

(Отметим на всякий случай, что все вхождения символа х в Ф заменяются на Ψ, так сказать, “одновременно”: дело в том, что в слове Ψ тоже могут содержаться вхождения буквы х, но эти новые вхождения на Ψ уже не заменяются!)

Пусть теперь Ф и Ψ – формулы ИВ, а А – некоторая его переменная. Тогда правило подстановки r₂ формулируется так:

r₂ (Ф) = S^А_ Ф.

Очевидно, что это – “параметрическое” правило; иными словами, имеется целое семейство правил подстановки, зависящее от двух параметров, переменной А и формулы Ψ. Применять можно любое из них.

Пример формального вывода в ИВ

Мы построим т.н. комментированный вывод, указывая справа в скобках основания, по которым та или иная формула занимает в нашем выводе соответствующее место.

Ф1: А  (В  А) (акс. А1)

Ф2: (А  (В  С))  ((А  В)  (А  С))) (акс. А2)

Ф3: (А  (В  А))  ((А  В)  (А  А))) (S^С_А Ф₂)

Ф4: (А  В)  (А А) (r₁ (Ф₁, Ф₃))

Ф5: (А  (В  А))  (А А) (S^В_ВА Ф₄)

Ф6: А  А (r₁ (Ф₁, Ф₅))

Согласно данным определениям, наш вывод является выводом формулы А А. Построив этот вывод, мы доказали, что

 _ИВ (А  А).

Отсюда немедленно следует, что, какова бы ни была формула  в ИВ,

 _ИВ (Ψ  Ψ)

(достаточно только что построенный вывод дополнить еще одним применением правила подстановки).

Отметим некоторые свойства выводов (их доказательства представляются очевидными). Хотя мы формулируем их в разделе, посвященном ИВ, они справедливы для любого формального исчисления.

1. Всякий вывод открывается одной из аксиом.

2. Начальный отрезок всякого вывода является выводом. т.е., если

Ф₁, Ф₂, …, Ф_к, …, Ф_n –

вывод, то и

Ф₁, Ф₂, …, Ф_к –

тоже вывод.

3. Если

Ф₁, Ф₂, …, Ф_n, и Ψ₁, Ψ₂, …, Ψ _m –

выводы, то и последовательность

Ф₁, Ф₂, …, Ф_n, Ψ₁, Ψ₂, …, Ψ_m –

тоже вывод.

4. Свойство 3 говорит, что, приписав один вывод за другим, мы получим снова вывод. Это утверждение можно обобщить: пусть Ф₁, …, Ф_n и ₁, …, _m – выводы; тогда всякая последовательность

X₁, X₂, …, X_m+n,

для которой из того, что

X_i = Ф_i´, X_j´ = Ф_j´, i < j, или

X_i = Ψ_i´, X_j = Ψ_j´, i < j,

следует, что i´ < j´, сама является выводом.

Формула A называется выводимой из множества формул Г(следствием множества формул Г) в данной теории, если существует последовательность A₁,...A_n формул такая, что A_n есть A и для любого i формула A_i есть либо аксиома, либо одна из формул множества Г, либо непосредственное следствие предыдущих формул последовательности по одному из правил вывода. В этом случае последовательность формул A₁,...A_n называется выводомформулы A из Г. Формулы множества Г называются гипотезами (допущениями, посылками) вывода.

Для сокращения записи утверждения "A есть следствие множества формул Г" употребляется обозначение  . Если множество Г конечно, Г={B₁,...B_n}, то вместо {B₁,...B_n}  пишут B₁,...B_n. Если Г- пустое множество (вывод является доказательством), то пишут , что равнозначно утверждению "A есть теорема".

Правила вывода можно подразделить на общие (работающие в любых аксиоматических теориях) и частные (работающие в теориях определенного типа). Приведем несколько общих правил, применяемых для построения доказательств и выводов в любых теориях.

1. Правило повторения посылки: .

2. Правило введения посылки:  если , то .

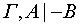3. Правило удаления посылки: если 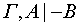 и , то .

4. Правило силлогизма: если  то 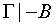.