
- •[Править]Математическая логика
- •Основные понятия
- •Построение таблиц истинности сложных высказываний. Приоритет логических операций
- •1) Инверсия 2) конъюнкция 3) дизъюнкция 4) импликация и эквивалентность
- •Как составить таблицу истинности?
- •Определить количество строк и столбцов в таблице истинности.
- •Начертить таблицу и заполнить заголовок
- •Заполнить первые n столбцов.
- •Заполнить остальные столбцы.
1.
Логика высказываний (или пропозициональная логика от англ. propositional logic, или исчисление высказываний[1]) — это формальная теория, основным объектом которой служит понятие логического высказывания. С точки зрения выразительности, её можно охарактеризовать как классическую логику нулевого порядка.
Несмотря на свою важность и широкую сферу применения, логика высказываний является простейшей логикой и имеет очень ограниченные средства для исследования суждений[1].
В логике логическими операциями называют действия, вследствие которых порождаются новые понятия, возможно с использованием уже существующих. В более узком,формализованном смысле, понятие логической операции используется в математической логике и программировании.
Логические операции с понятиями — такие мыслительные действия, результатом которых является изменение содержания или объёма понятий, а также образование новых понятий.
К операциям, которые связаны преимущественно с изменением содержания понятий, относятся:
-
отрицание;
-
ограничение ;
-
обобщение ;
-
деление.
К операциям, которые связаны преимущественно с объёмами понятий, относятся:
-
сложение;
-
умножение;
-
вычитание.
Данные операции могут быть записаны математически с помощью теории множеств.
Переход же к математической логике связан с понятием суждений и установлением операций над ними с целью получения сложных суждений.
[Править]Математическая логика
Логическая операция (логический оператор, логическая связка, пропозициональная связка) — операция над высказываниями, позволяющая составлять новые высказывания путем соединения более простых[1].
В
качестве основных обычно
называют конъюнкцию (![]() или
&), дизъюнкцию (
или
&), дизъюнкцию (![]() ), импликацию (
), импликацию (![]() ), отрицание (
), отрицание (![]() ).
В смысле классической
логики логические
связки могут быть определены через алгебру
логики.
В асинхронной секвенциальной
логике определена
логико-динамическая связка в виде
операции венъюнкции (
).
В смысле классической
логики логические
связки могут быть определены через алгебру
логики.
В асинхронной секвенциальной
логике определена
логико-динамическая связка в виде
операции венъюнкции (![]() ).
).
Основные понятия
Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, и(пропозициональная) формула, определяемой индуктивно следующим образом[2]:
-
Если P — пропозициональная переменная, то P — формула.
-
Если A — формула, то
 —
формула.
—
формула. -
Если A и B — формулы, то
 ,
, 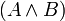 и
и 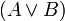 —
формулы.
—
формулы. -
Других формул нет.
Множество пропозиционных формул называется языком логики высказываний (англ. propositional language, PL)[2].
Знаки ![]() и
и ![]() (отрицание, конъюнкция, дизъюнкция и импликация)
называются пропозициональными
связками. Подформулой называется
часть формулы, сама являющаяся
формулой. Собственной
подформулой называется
подформула, не совпадающая со всей
формулой.
(отрицание, конъюнкция, дизъюнкция и импликация)
называются пропозициональными
связками. Подформулой называется
часть формулы, сама являющаяся
формулой. Собственной
подформулой называется
подформула, не совпадающая со всей
формулой.
Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных (то есть, при любой интерпретации)[4]. Вот несколько широко известных примеров тождественно истинных формул логики высказываний:
Законы де Моргана:
1) ![]() ;
;
2) ![]() ;
;
Закон контрапозиции:
![]() ;
;
Законы поглощения:
1) ![]() ;
;
2) ![]() ;
;
Законы дистрибутивности:
1) ![]() ;
;
2) ![]()
2.
Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.
Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:
1) переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;
2) соединяющие их проводники;
3) входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.
Простейшая
схема содержит один переключатель Р и
имеет один вход А и
один выход В.![]()
![]()
![]() Переключателю Р поставим
в соответствии высказывание р,
гласящее: - “Переключатель Р замкнут
”. Если р истинно,
то импульс, поступающий на полюс А,
может быть снят на полюсе В без
потери напряжения, то есть схема
пропускает ток. Если р ложно,
то переключатель разомкнут и схема тока
не проводит. Таким образом, если принять
во внимание не смысл высказывания, а
только его значение, то можно считать,
что любому высказыванию может быть
поставлена в соответсвие переключательная
схема с двумя полюсами (двухполюсная
схема).
Переключателю Р поставим
в соответствии высказывание р,
гласящее: - “Переключатель Р замкнут
”. Если р истинно,
то импульс, поступающий на полюс А,
может быть снят на полюсе В без
потери напряжения, то есть схема
пропускает ток. Если р ложно,
то переключатель разомкнут и схема тока
не проводит. Таким образом, если принять
во внимание не смысл высказывания, а
только его значение, то можно считать,
что любому высказыванию может быть
поставлена в соответсвие переключательная
схема с двумя полюсами (двухполюсная
схема).
Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.
![]()
Так,
конъюнкции двух высказываний ![]()
![]() ставится
в соответствие схема:
ставится
в соответствие схема:
![]()
а дизъюнкции ![]() -
схема:
-
схема:

Так как любая формула может быть записана в ДНФ или КНФ, то ясно, что каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики.
Пример
1. По
данной формуле составить РКС ![]() .
.
Решение. Упростим данную формулу с помощью равносильных преобразований:
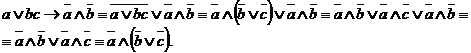
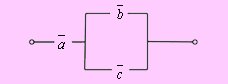
Тогда РКС для данной формулы имеет вид:
Пример 2. Упростить РКС:

Решение. Составим по данной РКС формулу (функцию проводимости) и упростим ее:
![]()
(к последним двум слагаемым применили закон поглощения).
Тогда упрощенная схема выглядит так:
![]()
3.
Две логические формулы называются равносильными, если при любых значениях входящих в них логических переменных эти формулы принимают одинаковые значения.
Равносильные формулы служат для выражения одних логических операций через другие, позволяют упрощать формулы или, точнее, заменять одни логические формулы другими, равносильными, но более простыми. В рассуждениях можно заменять сложные высказывания на более простые, равносильные им.
Легко показать равносильность АВ B, заменяющую операцию импликации на дизъюнкцию высказываний и B. Такое определение операции импликация рассматривалось еще в Древней Греции в IV в. до н.э. логиком Филоном из Мегары и было исключительно плодотворным.
Выше мы показали, что эквивалентность выражается через операции импликации и конъюнкцию, а импликация, в свою очередь, через дизъюнкцию и отрицание. Таким образом, любую логическую формулу можно заменить на равносильную, в которой используются только операции отрицания, дизъюнкции и конъюнкции. Это особенно важно для использования математической логики в электротехнике, где элементная база построена на применении трех булевых операций.
Общезначимость и выполнимость формул. Проблема разрешимости.
Определение 1.
Формула А логики предикатов называется выполнимой в области М, если существуют значения переменных входящих в эту формулу и отнесенных к области М (иначе – существует модель), при которых формула А принимает истинные значения.
Определение 2.
Формула А логики предикатов называется выполнимой, если существует область, на которой эта формула выполнима.
Определение 3.
Формула А логики предикатов называется тождественно-истинной в области М (выполнимой), если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.
Определение 4.
Формула А логики предикатов называется общезначимой, если она тождественна истинна на всякой области (на любой модели).
Если две равносильные формулы логики
предикатов соединить знаком эквиваленции
![]() ,
то полученная формула будет принимать
значение И для любого набора переменных
в любой области, т.е. будет общезначимой.
,
то полученная формула будет принимать
значение И для любого набора переменных
в любой области, т.е. будет общезначимой.
Это понятие является обобщением понятия тождественной истинности формулы логики высказываний. Все логические законы, представленный в логике высказываний формулами (1 -30) являются общезначимыми формулами логики предикатов и выражают, как и другие общезначимые формулы, законы логики на языке логике предикатов.
Наиболее употребительные специфические законы логики предикатов, как было отмечено выше, представлены формулами (31 -54).
Общезначимость формулы логики предикатов,
например, F обозначается ├F. Все
общезначимые формулы могут быть
источниками новых ├ формул. Например,
подставляя в (14) – закон исключенного
третьего
![]() – вместо х предикат Р(х1,…,хn),
получаем общезначимую формулу
Р(х1,…,хn)
– вместо х предикат Р(х1,…,хn),
получаем общезначимую формулу
Р(х1,…,хn)![]() (х1,…,хn).
При n=1 имеем общезначимую формулу
(х1,…,хn).
При n=1 имеем общезначимую формулу
![]() ,
и, таким образом ,
,
и, таким образом ,![]() -
общезначимая формула логики предикатов.
-
общезначимая формула логики предикатов.
Из тождественно истинной формулы логики
высказываний (2)
![]() подстановкой вместо х предиката Р(х,
y), а вместо y- предиката Q(x,y) получаем
общезначимую формулу
подстановкой вместо х предиката Р(х,
y), а вместо y- предиката Q(x,y) получаем
общезначимую формулу
![]() и т. д.
и т. д.
Определение 5.
Формула А логики предикатов называется тождественно ложной в области М, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области (иными словами, на данной модели).
Определение 6.
Формула А логики предикатов называется тождественно ложной (невыполнимой), если она тождественно ложна на всякой области (на всякой модели).
Например, формула
![]() является тождественно ложной (невыполнимой)
формулой логики предикатов.
является тождественно ложной (невыполнимой)
формулой логики предикатов.
Из приведенных определений с очевидностью следует:
-
Если формула А общезначима, то она и выполнима на всякой области (модели).
-
Если формула А тождественно истинна в области М, то она и выполнима в этой области .
-
Если формула А тождественно ложна в области М , то она не выполнима в этой области .
-
Если формула А не выполнима, то она тождественно ложна на всякой области (на всякой модели).
-
Для того, чтобы формула А логики предикатов была общезначима, необходимо и достаточно, чтобы ее отрицание было не выполнимо.
-
Для того, чтобы формула А логики предикатов была выполнимой, необходимо и достаточно, чтобы формула
 была не общезначима.
была не общезначима.
Рассмотрим пример
Пример
Доказать равносильность (логическое тождество):
![]() Заметив, что в каждой из кванторных
подформул обе предметные переменные
связаны и что, таким образом, они являются
высказываниями, введем обозначения:
Заметив, что в каждой из кванторных
подформул обе предметные переменные
связаны и что, таким образом, они являются
высказываниями, введем обозначения:
А=![]() ,
,
В=![]() или обозначив первую и вторую предметные
переменные через n1 и n2, соответственно:
или обозначив первую и вторую предметные
переменные через n1 и n2, соответственно:
А=![]() В=
В=![]()
В этих обозначениях заданное для
рассмотрения тождество будет выглядеть
так:
![]() .
.
Произведя равносильные преобразования,
можем убедиться в справедливости этого
тождества:
![]()
Если охарактеризовать рассматриваемое выражение в целом, то видим, что это общезначимая формула.
Пример
Определить тип формулы
![]() .
.
Пусть Р(х) : “ Число х - четно –” предикат, определенный в М=N2.
Таким образом, рассматриваемая формула на данной модели представляет собой следующее утверждение: “ Среди натуральных чисел существуют как четные, так и нечетные ”. Очевидно, что это высказывание истинно и, таким образом, на данной модели формула F тождественно истинна.
Однако, если этот же предикат задать на множестве M=NхN,где N – множество четных чисел, то формула F на такой модели окажется тождественно ложной.
Учитывая изложенное, заключаем, что рассматриваемая формула F выполнима (но не общезначима).
Пример
Для формулы
![]() подобрать
модель, на которой она является
тождественно истинной (и, таким образом,
в целом выполнимой).
подобрать
модель, на которой она является
тождественно истинной (и, таким образом,
в целом выполнимой).
Пусть Р(x, x, y): “x·x=y”, или иначе “x2=y” – предикат, определенный на множестве натуральных чисел, т.е. М=N. Тогда рассматриваемая формула выражает утверждение о существовании натурального квадрата натурального числа, что, очевидно, является истиной, т.е. на данной модели формула тождественно истинна, что и требовалось доказать.
Пример
Рассмотрим формулу
![]() .
Это выполнимая формула. Действительно,
если Р(х, y, x): “x+y=x” – предикат суммы,
то на M=N существует подстановка вместо
y соответствующего значения, дающего
значение истинности данной формуле.
Очевидно, это y=0, поскольку в этом случае
получаем “х=х”.
.
Это выполнимая формула. Действительно,
если Р(х, y, x): “x+y=x” – предикат суммы,
то на M=N существует подстановка вместо
y соответствующего значения, дающего
значение истинности данной формуле.
Очевидно, это y=0, поскольку в этом случае
получаем “х=х”.
Если же P(x, y, x): “xy=x” – предикат
произведения, то таким значением y
является y=1, так как при нем получаем
истинное высказывание
![]() .
.
Но это единственные подстановки, приводящие к верным утверждениям, что и говорит именно о выполнимости данной формулы (но не об ее общезначимости).
Пример
Является ли общезначимой формула:
![]()
![]() ?
?
Пусть P(x, y) – предикат порядка (бинарного
отношения ) “![]() ”,
определенный на конечном множестве
натуральных чисел M1. Тогда при
подстановке в формулу вместо свободной
переменной y величины
”,
определенный на конечном множестве
натуральных чисел M1. Тогда при
подстановке в формулу вместо свободной
переменной y величины
![]() мы получим истинное утверждение, а при
подстановке любой другой константы из
множества М1 – ложное. Таким
образом, рассматриваемая формула не
является общезначимой.
мы получим истинное утверждение, а при
подстановке любой другой константы из
множества М1 – ложное. Таким
образом, рассматриваемая формула не
является общезначимой.
Пример
Рассмотрим формулу
![]() .
Покажем, что она невыполнима.
.
Покажем, что она невыполнима.
Допустим противное, т.е. что она выполнима.
Это означает, что существует такое
множество М и такой конкретный предикат
![]() в нем, что когда
в нем, что когда
![]() ,
то данная формула превращается в такой
конкретный предикат
,
то данная формула превращается в такой
конкретный предикат
![]() ,
который, в свою очередь, превращается
в истинное высказывание при всякой
подстановке вместо y элементов из
множества М. Возьмем любое
,
который, в свою очередь, превращается
в истинное высказывание при всякой
подстановке вместо y элементов из
множества М. Возьмем любое![]() .
Тогда высказывание
.
Тогда высказывание
![]() истинно, как мы только что установили.
Следовательно, истинны высказывания
истинно, как мы только что установили.
Следовательно, истинны высказывания
![]() и
и
![]() .
.
Из истинности второго высказывания
заключаем, что высказывание
![]() истинно (поскольку “для всех предметных
переменных”, как бы они ни обозначались).
Но это противоречит истинности первого
высказывания
истинно (поскольку “для всех предметных
переменных”, как бы они ни обозначались).
Но это противоречит истинности первого
высказывания
![]() .
.
Таким образом, наше предположение о выполнимости формулы неверно.
Проблема разрешимости в логике предикатов ставится так же, как и в алгебре логики: существуют ли алгоритмы, позволяющие для любой формулы А логики предикатов установить, к какому типу (классу) она относится, т.е. является ли она общезначимой, выполнимой или тождественно ложной (невыполнимой). Если бы такой алгоритм существовал, то, как и в алгебре высказываний, он сводился бы к критерию тождественной истинности любой формулы логики предикатов. Отметим, что, в отличие от алгебры логики, в логике предикатов не применим метод перебора всех вариантов значений переменных, входящих в формулу, так как таких вариантов может быть бесконечное множество.
4.
