
- •Поиск и включение для деревьев
- •Исключение из деревьев
- •Сбалансированные деревья
- •Включение элементов в сбалансированное дерева.
- •1 Случай
- •2 Случай
- •Исключение из балансированного дерева (авл)
- •Критерии и оценки алгоритма. Общие методы.
- •Асимптотические характеристики
- •Роль и методы в снижении трудоемкости решения задачи
- •Структура данных для описания решетки.
- •Частные характеристики качества алгоритмов
- •Увеличение быстродействия программ
- •Хеширование
- •Хеш таблицы.
- •Хеш функции
- •Двойное хеширование
- •Идеальное хеширование
- •Алгоритмы для работы с графами
- •Деревья поиска в ширину
- •Поиск в глубину
- •Стягивающие или остовные деревья
- •Минимальное остовное дерево
- •Эйлоровый цикл
- •Гомельтоновый цикл
- •Кротчайшие пути в ориентированных графах.
- •Комбинаторика
Двойное хеширование
Один из лучших способов. Т.к. получаемые при этом перестановки обладают многими характеристики случайно выбираемых перестановок.
H(k,i)=(h1(k)+i*h2(k)) h1,h2 вспомогательные функции.
В этой методике первая ячейка вычисляется T[h1(k)] смещение каждой последовательной h2(k) mod m
В отличие от предыдущих методов в каждом случае зависит от ключа k по 2 параметрам. Выбор начальной ячейки и расстояние между двумя ячейками исследования.
M=13 h1(k)=k mod 13 h2(k)=1+(k mod 11) k=14
|
|
|
79 |
|
|
|
|
|
69 |
|
98 |
|
|
|
72 |
|
|
|
|
|
|
|
50 |
|
|
H1(k)=14 mod 13=1
1+14 mod 11=1+3=4 i=1+4=5
5+4=9
Чтобы последовательность исследований могла охватить всю таблицу значение h2(k) должно быть взаимно простым.
Идеальное хеширование
Методика, которая в наихудшем случае выполняет поиск за величину 0(1). Такую ситуацию дает статическое множество ключей т.е. после того как все ключи сохранены в таблицы их множество никогда не изменяется. Используем двухуровневую схему хеширования с универсальным хешированием на каждом уровне. Первый уровень хеширования по сути тот же, что и в схеме с цепочками. N ключей хешируем в m ячеек с использованием хеш функции h выбранные из семейств универсальных хеш функций. Но вместо создания списка ключей, хешированных в j ячейку мы используем вторичную хеш таблицу sj. Она довольно маленькая имеет свою функцию hj
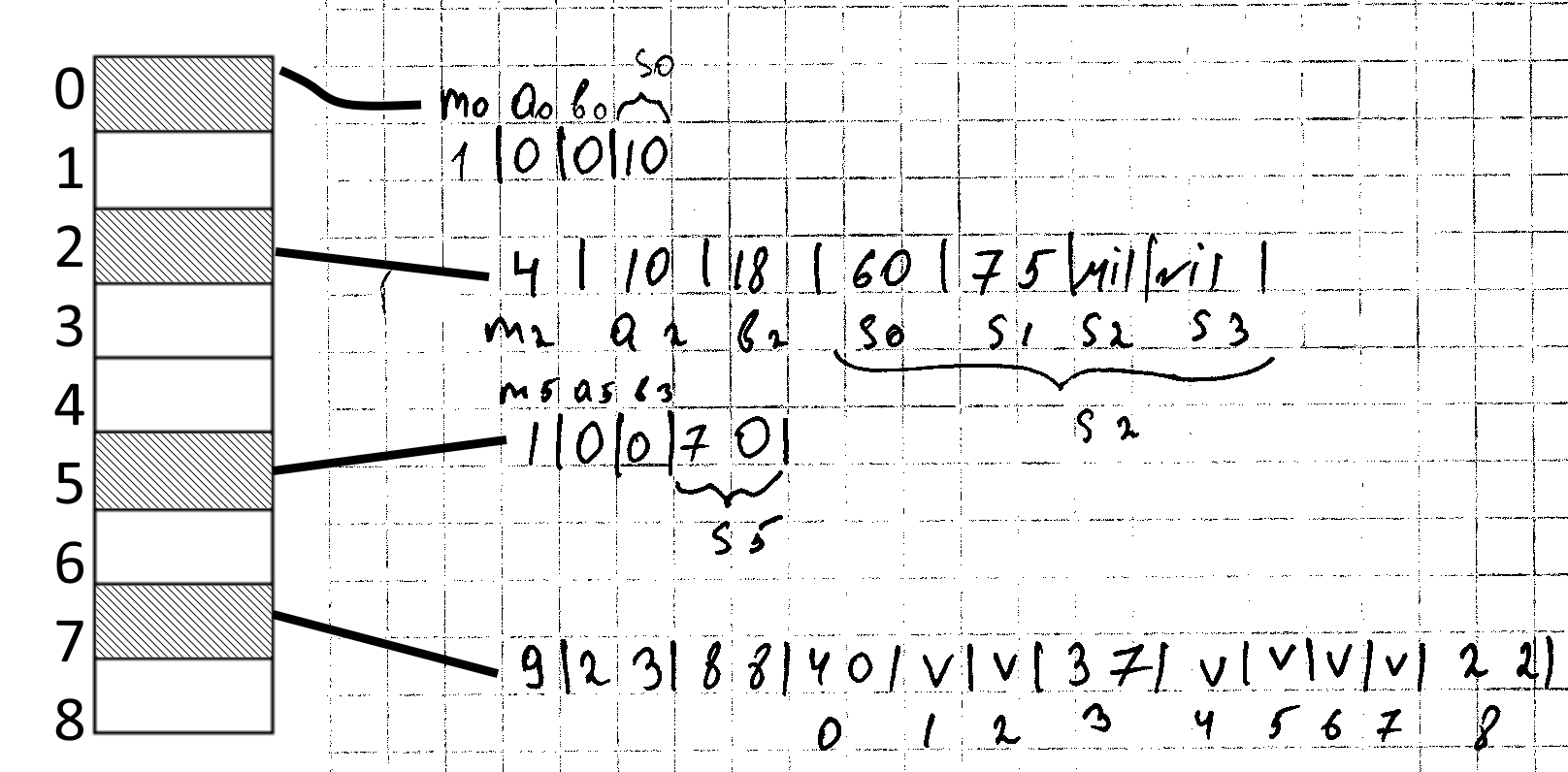
Hj(k)=(aj*k+bj) mod p)mod mj h(75)= ((10*75+18)mod 101)mod 4=1
{10,22,37,40,60,70,75}
Сохранить в хеш таблице
H(k)=((a*k+b) mod p)mod m a=3; b=42; p=101; m=9 h(10)=((3*10+42) mod 101) mod 9= 0 h(22)=(108 mod 101) mod 9=7 h(37)=7 h(40)=7 h(60)=2 h(70)=5 h(72)=2
Размер хеш таблицы
Вторичная таблица sj хранит все ключи хеширование в ячейку j. Размер ? ни в одной из вторичных таблиц нет коллизии. В справочнике кнута есть рекомендации по выбора размера вторичной таблицы В любом случае mj зависит от nj
Алгоритмы для работы с графами
Представление графов.
Существует 2 стандартных способа
G=(V,E)
Набор цепных списков смежных вершин
Матрица смежности
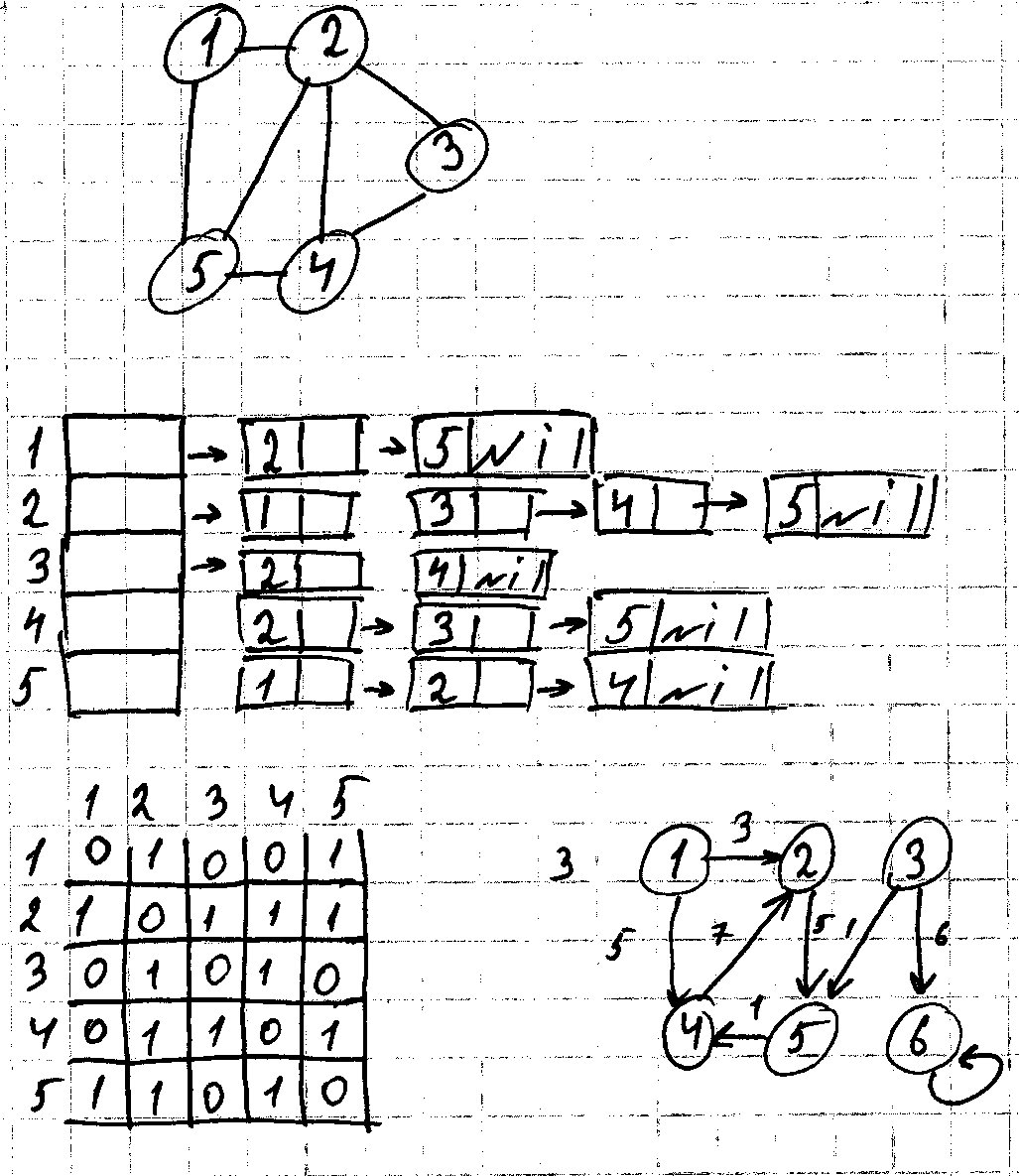
ЕСЛИ Количество ребер намного меньше ?то спискам смежности. С помощью матриц смежности отображают ?
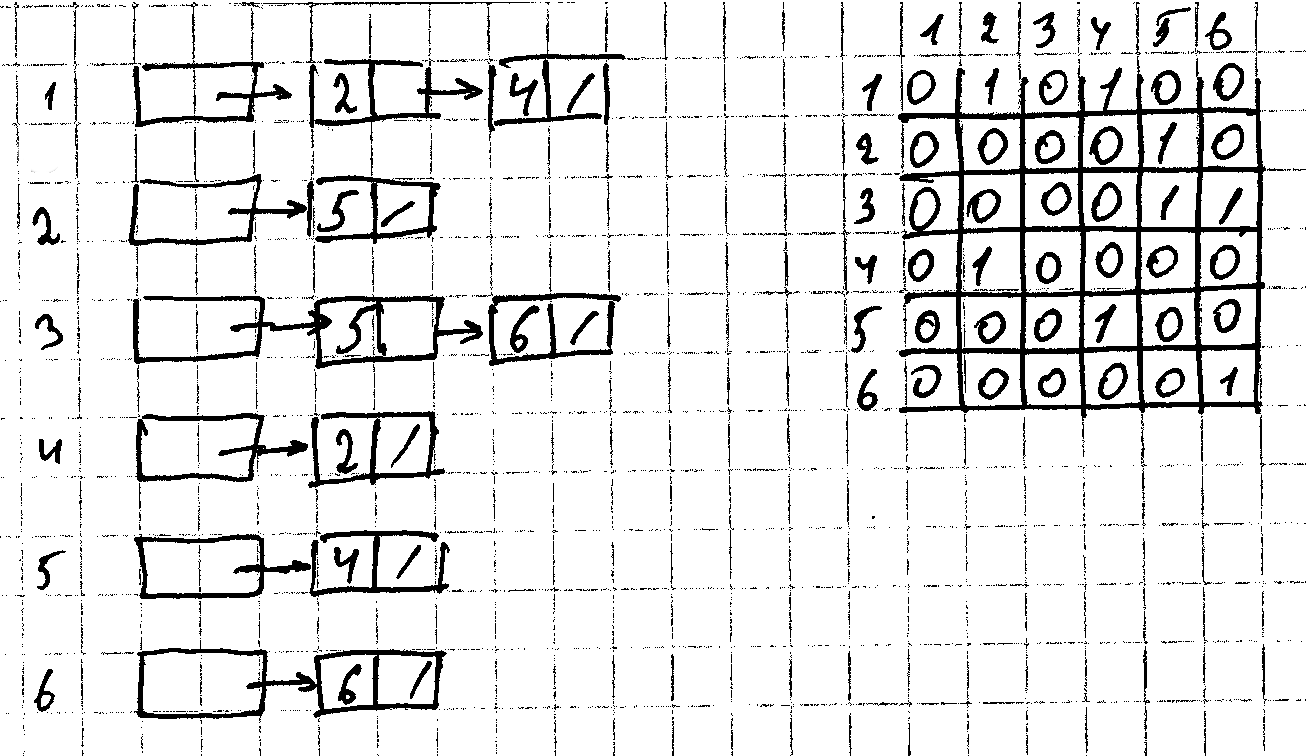
![]()
Или когда для нас в приоритете скорость поиска. Алгоритм определения кратчайшего пути используют матрицу смежности. Представление графов в виде списков смежности Adj массив из |V|. Каждый элемент массива Adj[u] состоящий из вершин. Вершины в списке появляются в произвольном порядке. Если j ориентированный граф, то сумма длин всех его списков смежности равна количеству ребер. Ребру (u,v) однозначно соответствует элемент v в списке adj[u]. Неориентированное ребру uv появляется в списке adj[u] как v, а в списке adj[v] появляется как u. Для любых графов представление в виде списков смежности требует объем памяти пропорциональный (V+E). Списки смежности легко адаптируются для представление смешенных графов. Т.е. графов с каждом ребром которого связан определённый вес. Вес определяется весовой функцией w:E->R. Пусть adj взвешенный граф с весовой функцией w(u,v) хранится вместе с вершиной v в списке смежности ?. В матрице вместо единички ставится вес ребра. Простота матрицы смежности делает часто ее предпочтительнее для небольших графов. Для невзвешенных графов используют 1 бит. ?
Алгоритм поиска в ширину - это простейший алгоритм обхода графа. Обход графа – систематический перемещение по ребрам графа, при котором перемещается все вершины графа?.
Путь задан граф.
G=(V,E) S – исток
Алгоритм поиска в ширину ? для открытия всех вершин достижимых из S. При этом вычисляется расстояние от S истока до каждой достижимой из S вершины. В процессе обхода строится дерево поиска в ширину, с корнем S содержащие все достижимые вершины. Для каждой достижимой вершины U путь дерева поиска в ширину соответствует кратчайшему количеству ребер ?. Алгоритм одинаково работает для ориентированных и неориентированных графов. В процессе обхода мы идем в ширь. Т.е. прежде чем приступить к поиску k+1 мы должны обойти все вершин на расстоянии k. Поиск в ширину раскрашивает вершины графа в белый серый и черные цвета. Изначально все вершины белые. Позже они могут стать серыми, а затем черными. Когда вершина открывается в процессе поиск ,она окрашивается. Т.е. серые и черные это уже открытые вершины. Чтобы обеспечить заявленный порядок обхода.
(u,v) ∈ E вершина v либо серая либо черная. Т.е. все смежные с черной уже открыты. Серые вершины могут иметь белых соседей. Серые представляет собой границу между открытыми и неоткрытыми вершинами. Сначала дерево ? состоит только из источника S. Сканируем список смежности. Если в процессе сканирования для уже открытой вершины u открывается белая вершина v, то вершина v и ребро uv добавляется в дерево. U является родителем для v в этом дереве. Вершина может быть открыта не более 1 раза => 1 родитель.
Fsearch предполагает входной граф j с помощью списков смежности. В каждой вершине поддерживается дополнительная структура данных: цвет каждой вершины color[u] и предшественник хранится в массиве P[u] ?. Расстояние от s до вершины u хранится в поле d[u] Q - ?
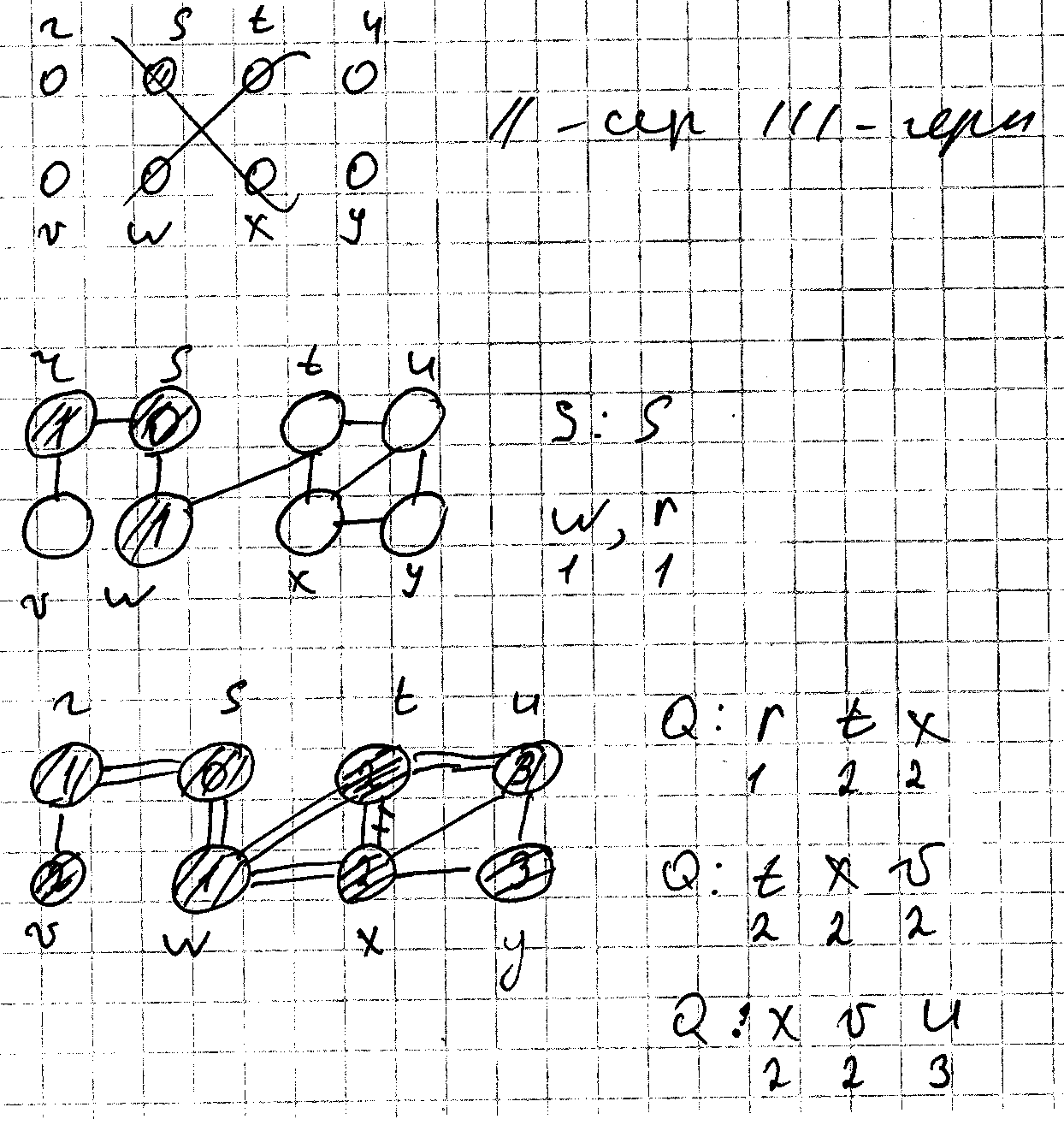
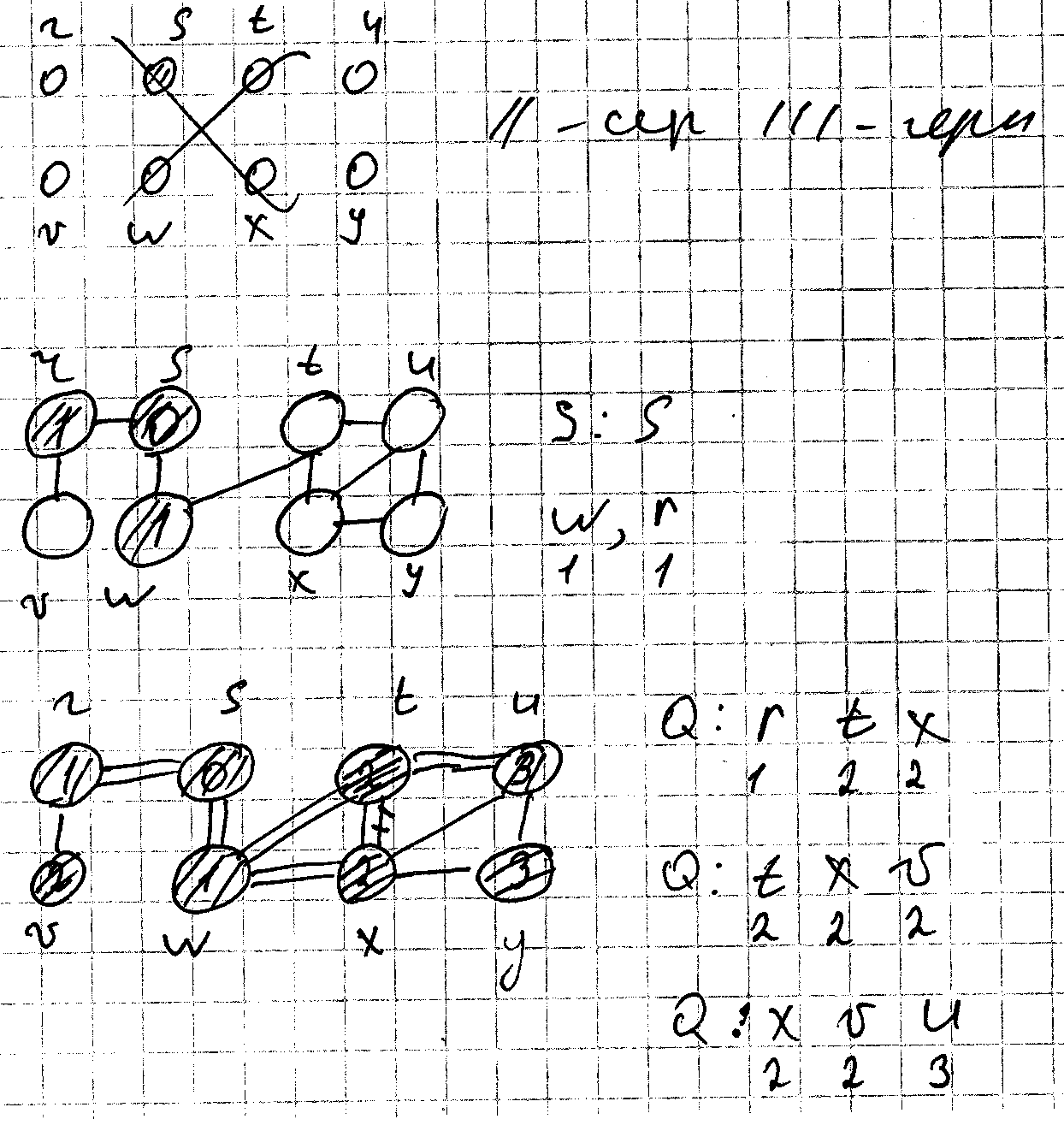
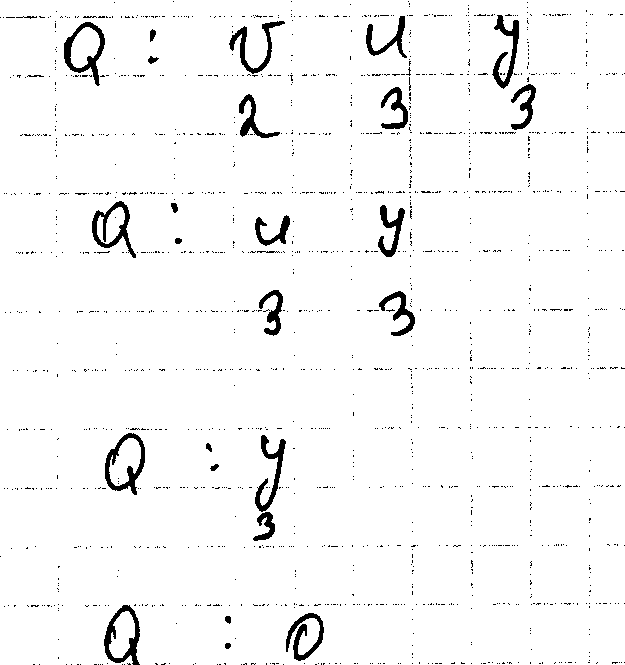
Procedure
Tsearch
(G,S)
Для всех u кроме S




Color [u]=white d[u]=0 p[u]=nil


Color [s]=Grey d[s]=0 p[s]=nil


H=hight(v) setlenght (Q,h) k=0 Q[k]=S


* -
Q=0
End
цикл будет пока очередь не является
пустой
+

U= элемент из головы Q

*
Для всех U э adj[u]
Color[u]=Black




-
Color[u]=white



+
Color [u]=grey d[u]=d[u]+1 p[u]=u u-> в конце очередь Q

Результат поиска в ширину мб разным, зависит от порядка просмотра. Дерево поиска в ширину могут клонироваться, расстояние d остаются одинаковыми.
